5.3. Фотоны и их свойства
Согласно современным представлениям, свет представляет собой сложное явление, сочетающее в себе свойства электромагнитной волны и потока частиц - фотонов. Такое двойственное сочетание свойств называется корпускулярно-волновым дуализмом.
Фотоном называется
элементарная частица - квант
электромагнитного поля. Отличие
фотона от других элементарных частиц
состоит в том, что фотон
всегда движется со скоростью
.
Масса фотона равна нулю: m
= 0.
Энергия фотона вычисляется по формуле (5.1)
или
,
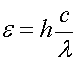где λ - длина волны света.
Импульс фотона равен
Таким образом, формулы (5.1) и (5.6) отражают корпускулярно-волновой дуализм фотонов. Подобно частице (корпускуле), фотон обладает энергией и импульсом, которые выражены через волновые характеристики: частоту и длину волны.
Дальнейшее развитие квантовые представления получили при объяснении закономерностей в спектре атома водорода.
5. 4. Закономерности в спектре атома водорода
Опыт показывает, что спектры невзаимодействующих атомов, как это имеет место для разреженных газов, состоят из отдельных линий, сгруппированных в серии. На рис. 5.3 показаны линии серии спектра атома водорода, расположенные в видимой области. Длина волны, соответствующая линиям в этой серии, называемой серией Бальмера, выражается формулой
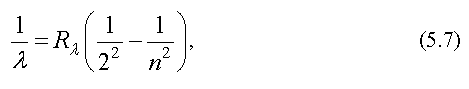
где, n
= 3, 4, 5, ...; 
- постоянная Ридберга.
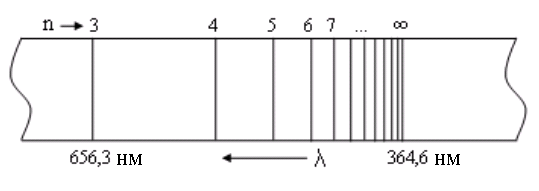
Рис. 5.3
Линия, соответствующая n = 3, является наиболее яркой и называется головной, а значению n = ∞ соответствует линия, называемая границей серии.
В других областях спектра (ультрафиолетовой, инфракрасной) также были обнаружены серии линий. Все они могут быть представлены обобщенной формулой Бальмера - Ридберга
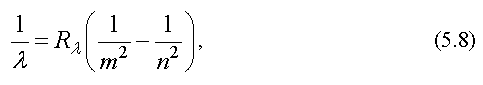
где m - целое число, постоянное для каждой серии.
При m = 1; n = 2,3,4, ... - серия Лаймана. Наблюдается в ультрафиолетовой области. При m = 2; n = 3,4,5, ... - серия Бальмера - в видимой области. При m = 3; n = 4,5,6, ... - серия Пашена - в инфракрасной (ИК) области. При m = 4; n = 5,6,7, ... - серия Брэкета - тоже в ИК области и т. д.
Дискретность в структуре атомных спектров указывает на наличие дискретности в строении самих атомов. Для энергии квантов излучения атомов водорода можно записать следующую формулу
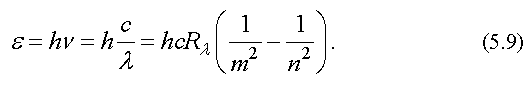
При записи этого выражения использованы формулы (5.1), (3.21) и (5.8). Формула (5.9) получена на основе анализа экспериментальных данных.
5.5. Постулаты Бора
Первая квантовая теория строения атома быда предложена в 1913 г. датским физиком Нильсом Бором. Она была основана на ядерной модели атома, согласно которой атом состоит из положительно заряженного ядра, вокруг которого вращаются отрицательно заряженные электроны. Теория Бора основана на двух постулатах.
I постулат Бора - постулат стационарных состояний. В атоме существуют стационарные (не изменяющиеся со временем) состояния, в которых он не излучает энергию. Этим стационарным состояниям соответствуют стационарные орбиты, по которым движутся электроны. Движение электронов по стационарным орбитам не сопровождается излучением энергии.
II постулат Бора получил название "правило частот". При переходе электрона с одной стационарной орбиты на другую излучается (или поглощается) квант энергии, равный разности энергий стационарных состояний
где h - постоянная Планка; v - частота излучения (или поглощения) энергии; hv - энергия кванта излучения (или поглощения); En и Em - энергии стационарных состояний атома до и после излучения (поглощения), соотвественно. При Em < En происходит излучение кванта энергии, а при Em > En - поглощение.
По теории Бора значение энергии электрона в атоме водорода равно
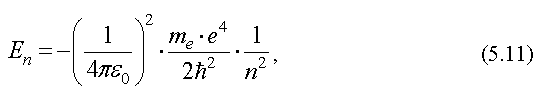
где me
- масса электрона,
e - заряд электрона,
εe
- электрическая постоянная ,
,
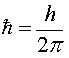h - постоянная Планка,
n - целое число, n = 1,2,3,...
Таким образом, энергия электрона в атоме представляет собой дискретную величину, которая может изменяться только скачком.
Набор возможных дискретных частот квантовых переходов определяет линейчатый спектр атома
Вычисленные по этой формуле частоты спектральных линий для водородного атома оказались в прекрасном согласии с экспериментальными данными. Но теория не обясняла спектры других атомов (даже следующего за водородом гелия). Поэтому теория Бора была только переходным этапом на пути построения теории атомных явлений. Она указывала на неприменимость классической физики к внутриатомным явлениям и главенствующее значение квантовых законов в микромире.