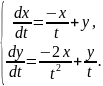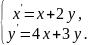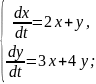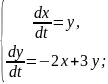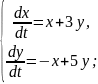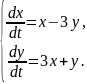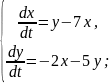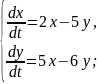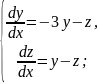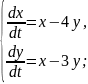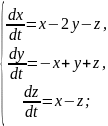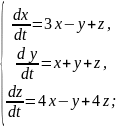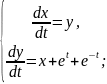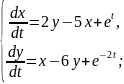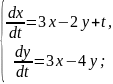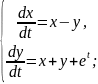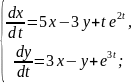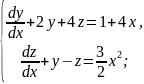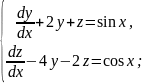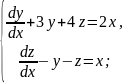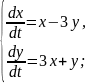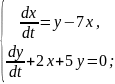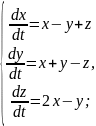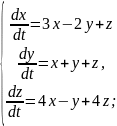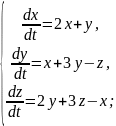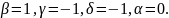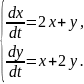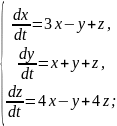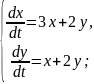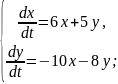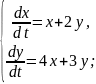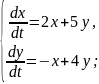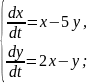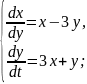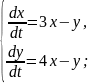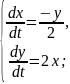ЗМІСТ
Заняття №14. Метод виключення інтегрування
системи диференціальних рівнянь……………………………………………….6
Заняття №15. Загальний розв’язок лінійної
однорідної системи звичайних диференціальних рівнянь……………………13
Самостійна робота №4…………………………………………………………..23
Заняття №16. Метод Лагранжа………………………………………………….25
Контрольна робота №2………………………………………………………….35
Відповіді………………………………………………………………………….41
Література………………………………………………………………………..50
Заняття №14
Тема. Метод виключення інтегрування системи диференціальних рівнянь (2 год.)
Теоретичний блок
Система диференціальних рівнянь називається лінійною, якщо вона лінійна відносно всіх невідомих функцій та їх похідних.
Нормальна лінійна однорідна система n-го порядку має вигляд

В
області неперервності коефіцієнтів
 система
задовольняє умови теореми існування і
єдності розв’язку задачі Коші.
система
задовольняє умови теореми існування і
єдності розв’язку задачі Коші.
Фундаментальною системою розв’язків вказаної вище системи називається сукупність n лінійно незалежних розв’язків цієї системи
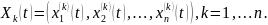
Загальний розв’язок однорідної системи диференціальних рівнянь представляється у вигляді

де
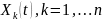 – фундаментальна
система розв’язків цієї системи,
– фундаментальна
система розв’язків цієї системи,
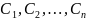 - довільні сталі.
- довільні сталі.
Нормальна лінійна неоднорідна система n-го порядку має вигляд
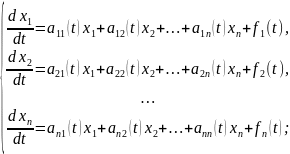
де
хоча б одна із функцій
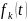 тотожно
не дорівнює нулю.
тотожно
не дорівнює нулю.
Загальний розв’язок неоднорідної системи диференціальних рівнянь представляється у вигляді
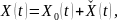
де
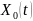 – загальний розв’язок відповідної
однорідної системи,
– загальний розв’язок відповідної
однорідної системи,
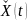 - деякий частинний розв’язок заданої
неоднорідної системи.
- деякий частинний розв’язок заданої
неоднорідної системи.
Одним із методів розв’язання лінійних систем диференціальних рівнянь є метод виключення, оснований на зведенні системи до одного диференціального рівняння n-го порядку.
Приклад. Розв’язати систему диференціальних рівнянь

Запишемо систему у вигляді

З
першого рівняння системи знаходимо
 :
:

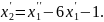
Підставимо
та
 у друге рівняння системи:
у друге рівняння системи:

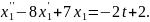
Це лінійне неоднорідне диференціальне рівняння другого порядку зі сталими коефіцієнтами. Відповідне йому однорідне рівняння
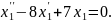
Характеристичне рівняння

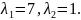
Загальний розв’язок однорідного рівняння

Частинний розв’язок неоднорідного рівняння шукаємо у вигляді:

Підставляємо це у перетворене неоднорідне диференціальне рівняння:

Прирівняємо
коефіцієнти при однакових степенях
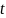 :
:
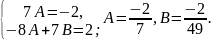
Отже,
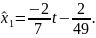
Загальний розв’язок диференціального рівняння представляється у вигляді:
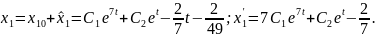
Підставимо
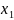 та
та
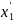 у перше рівняння:
у перше рівняння:


Отже, загальний розв’язок заданої неоднорідної системи такий:
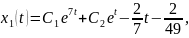
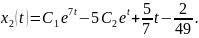
Практичний блок
Система диференціальних рівнянь розв’язана методом виключення. Заповніть пропуски.
Розв’язання
Перепишемо перше рівняння системи таким чином:
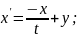

Підставимо
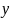 та
та
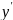 у друге рівняння системи
у друге рівняння системи

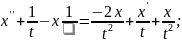
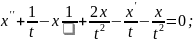

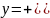
Отже, загальний розв’язок системи диференціальних рівнянь

Відповідь:____________________________________________________
Розв’язання
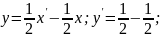
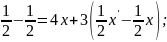
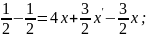
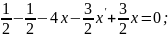

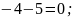
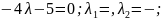


Отже,
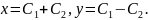
Відповідь:____________________________________________________
Знайти розв’язок системи диференціальних рівнянь:
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:____________________________________________________
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:____________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:____________________________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________
Відповідь:____________________________________________________
Блок завдань для самостійного опрацювання
Знайти розв’язок системи диференціальних рівнянь:
Довгострокові завдання
Знайти розв’язок системи диференціальних рівнянь:
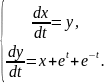
Заняття №15
Тема. Загальний розв’язок лінійної однорідної системи звичайних диференціальних рівнянь (2 год.)
Теоретичний блок
Лінійна однорідна система звичайних диференціальних рівнянь має вигляд:
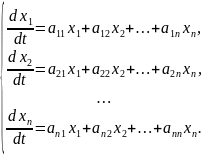
Де
 – сталі,
- аргумент, функції
– сталі,
- аргумент, функції
 – шукані
функції.
– шукані
функції.
Розв’яжемо дану систему методом Ейлера.
Розв’язок шукають у вигляді:
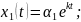

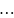

Підставимо його у систему
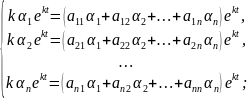
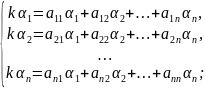

Складаємо визначник Вронського
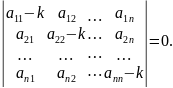
Це рівняння називається характеристичним рівнянням системи. Його корені називаються характеристичними коренями рівняння.
Розглянемо три випадки.
Корені характеристичного рівняння різні дійсні числа.
Приклад 1. Розв’язати систему диференціальних рівнянь
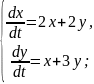
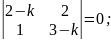

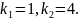
Характеристичні корені дійсні різні числа. Розв’язок системи шукають у вигляді:
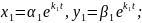

Складаємо
систему для


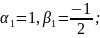
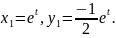
Складаємо
систему для
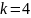


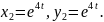
Отже, загальний розв’язок системи

Корені характеристичного рівняння різні. Серед них є два комплексно спряжені корені.
Приклад 2. Розв’язати систему диференціальних рівнянь
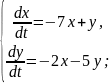


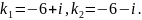
Характеристичні корені комплексно спряжені.

 визначають
підстановкою знайдених коренів у
вихідну систему рівнянь.
визначають
підстановкою знайдених коренів у
вихідну систему рівнянь.


Для

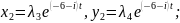
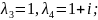
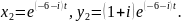
Розпишемо
і
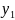 за властивостями комплексно спряжених
чисел.
за властивостями комплексно спряжених
чисел.
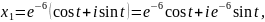
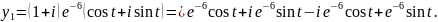
Аналогічні
дій виконаємо і для
та
 і візьмемо за систему часткових
розв’язків окремо дійсні частини.
і візьмемо за систему часткових
розв’язків окремо дійсні частини.

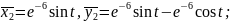
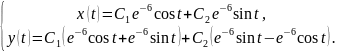
Корені характеристичного рівняння кратні дійсні числа.
Приклад 3. Розв’язати систему диференціальних рівнянь
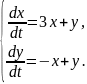
Складаємо характеристичне рівняння
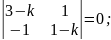
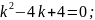
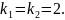
Корені характеристичного рівняння рівні, тому
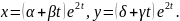
Для
знаходження
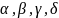 підставимо
шукані форми розв’язку у систему
рівнянь.
підставимо
шукані форми розв’язку у систему
рівнянь.
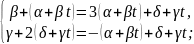
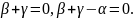
Із останньої умови випливає, що незалежними розв’язками є
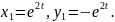
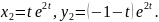
Загальний розв’язок запишемо у вигляді

Практичний блок
1. Система диференціальних рівнянь розв’язана методом Ейлера. Заповніть пропуски.
Розв’язання
Розв’язок системи шукаємо у вигляді
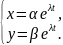
Підставимо даний розв’язок у систему
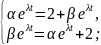


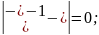

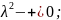

Для


Отримали однорідну систему, у який два рівняння еквівалентні.
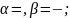
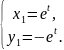
Для
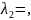
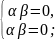
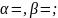


Відповідь:____________________________________________________
Розв’язання
Розв’язок системи шукаємо у вигляді
Підставимо даний розв’язок у систему
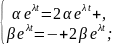
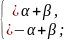
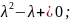
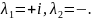
Для



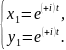
Для
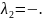
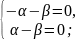

За властивостями комплексних чисел
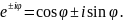
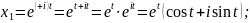
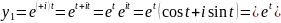

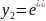
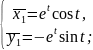
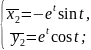
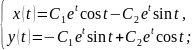
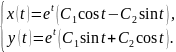
Відповідь:____________________________________________________
2. Знайти розв’язок системи диференціальних рівнянь методом Ейлера:
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:____________________________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:____________________________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:____________________________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:____________________________________________________
Блок завдань для самостійного опрацювання
Знайти розв’язок системи диференціальних рівнянь методом Ейлера:
Довгострокові завдання
Знайти розв’язок системи диференціальних рівнянь методом Ейлера: