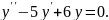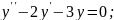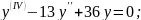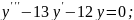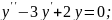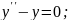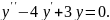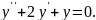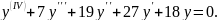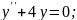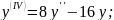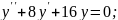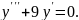Самостійна робота №2
Варіант
№1.

Варіант
№2.
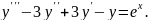
Варіант
№3.

Варіант
№4.

Варіант
№5.
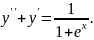
Варіант
№6.
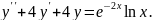
Варіант
№7.

Варіант
№8.
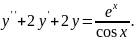
Варіант
№9.
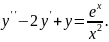
Варіант
№10.
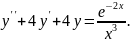
Варіант
№11.

Варіант
№12.

Варіант
№13.
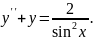
Варіант
№14.
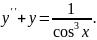
Варіант
№15.
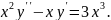
Варіант
№16.
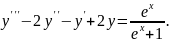
Варіант
№17.
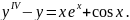
Варіант
№18.
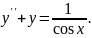
Варіант №19.
Варіант
№20.
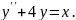
Варіант
№21.

Варіант
№22.
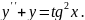
Варіант
№23.
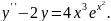
Варіант
№24.
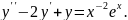
Варіант №25.
Варіант
№26.

Варіант №27.
Варіант №28.
Варіант
№29.
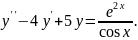
Варіант
№30.
Заняття №11
Тема. Розв’язування однорідних диференціальних рівнянь n-го порядку зі сталими коефіцієнтами у випадку n дійсних різних характеристичних коренів (2 год.)
Теоретичний блок
Розглянемо лінійне однорідне рівняння n-го порядку зі сталими коефіцієнтами, тобто рівняння виду
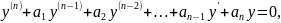
де
 – дійсні числа.
– дійсні числа.
Оскільки дане рівняння є лінійним однорідним, то для побудови його загального розв’язку достатньо знайти n лінійно незалежних частинних розв’язків (фундаментальну систему). Розв’язки рівняння шукатимемо у вигляді (метод Ейлера)
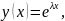 де
де
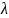 – деяка стала.
– деяка стала.
Знайдемо похідні

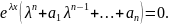
Вираз у дужках називається характеристичним многочленом
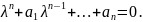
Як відомо дане рівняння має рівно n коренів, серед яких можуть бути дійсні і комплексно спряжені.
Розглянемо випадок, коли всі корені дійсні і різні.
Покажемо, що вони утворюють фундаментальну систему. Для цього обчислимо відповідний визначник Вронського:
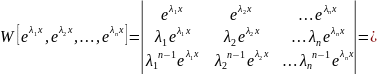
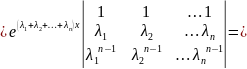

Таким чином, система розв’язків є фундаментальною і тому функція
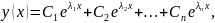
де
 – довільні сталі, буде загальним
розв’язком неоднорідного
диференціального
рівняння.
– довільні сталі, буде загальним
розв’язком неоднорідного
диференціального
рівняння.
Приклад.
Розв’язати рівняння

Складаємо характеристичне рівняння

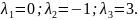
Отже,
характеристичні корені дійсні та різні.
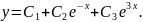
Практичний блок
3.Дано розв’язок однорідного диференціального рівняння. Заповніть пропуски.
Розв’язання
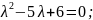
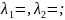

Відповідь:____________________________________________________
Розв’язання
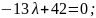

Відповідь:____________________________________________________
Розв’язання
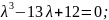
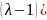


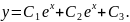
Відповідь:____________________________________________________
Розв’язання
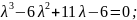

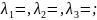

Відповідь:____________________________________________________
4.Знайти розв’язок однорідного диференціального рівняння:
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:____________________________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:____________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:____________________________________________________
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:____________________________________________________
Блок завдань для самостійного опрацювання
Знайти розв’язок однорідного диференціального рівняння:
Довгострокові завдання
Знайти розв’язок однорідного диференціального рівняння:
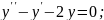
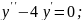

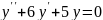 ;
;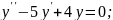

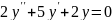 ;
;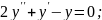

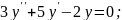
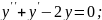
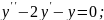
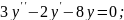
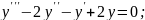
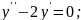
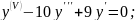
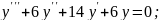
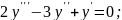
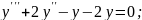
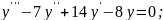
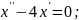


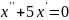 ;
;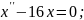
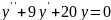 ;
;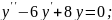

Заняття №12
Тема. Розв’язування однорідних диференціальних рівнянь n-го порядку зі сталими коефіцієнтами у випадку кратних характеристичних коренів та комплексних коренів (2 год.)
Теоретичний блок
Розглянемо лінійне однорідне рівняння n-го порядку зі сталими коефіцієнтами, тобто рівняння виду
де – дійсні числа.
Розглянемо випадок комплексно спряжених коренів.
Як відомо кожну комплексну функцію дійсного аргументу завжди можна подати у вигляді
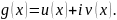
Має місце наступна Лема.
Лема.
Якщо функція
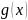 є розв’язком однорідного диференціального
рівняння, то окремо кожна із функцій
є розв’язком однорідного диференціального
рівняння, то окремо кожна із функцій
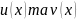 теж є розв’язками даного рівняння.
теж є розв’язками даного рівняння.
Нехай
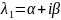 –
комплексний корінь.
–
комплексний корінь.

Згідно
поданій вище Лемі, кожна із частин
розв’язку теж є розв’язком, тобто
розв’язками будуть функції:
 .
.
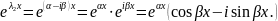
Згідно
поданій вище Лемі, розв’язками є:
 .
.
Отже, парі комплексних коренів відповідає пара дійсних функцій дійсних змінних:

У випадку, якщо характеристичне рівняння має такі корені, що повторюються, то кажуть, що існують кратні корені (кратність коренів – кількість його появи серед розв’язків).
Якщо
є характеристичний корінь кратності
k,
то даному кореню відповідає система
функцій:
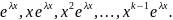
А
загальний розв’язок має вигляд:
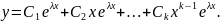
Приклад 1. Знайти розв’язок рівняння:

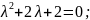
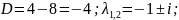
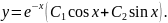
Приклад 2. Розв’язати рівняння

 – кратність
коренів 3.
– кратність
коренів 3.
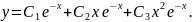
Практичний блок
Дано розв’язок однорідного диференціального рівняння. Заповніть пропуски.
Розв’язання
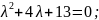
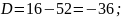
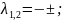
Відповідь:____________________________________________________
Розв’язання
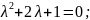

Відповідь:____________________________________________________
Розв’язання

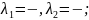
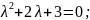
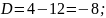
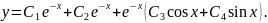
Відповідь:____________________________________________________
 .
.
Розв’язання
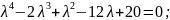


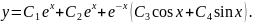
Відповідь:____________________________________________________
Знайти розв’язок однорідного диференціального рівняння:
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________
Відповідь:____________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________
Відповідь:____________________________________________________
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________
Відповідь:____________________________________________________
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________
Відповідь:____________________________________________________
Блок завдань для самостійного опрацювання
Знайти розв’язок однорідного диференціального рівняння:
Довгострокові завдання
Знайти розв’язок однорідного диференціального рівняння:
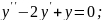
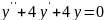 ;
;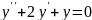 ;
;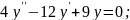
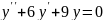 ;
;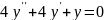 ;
;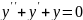 ;
;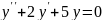 ;
;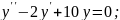
 ;
;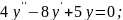
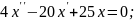
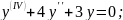
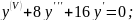
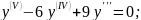
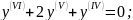

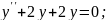
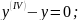
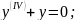

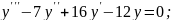


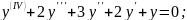

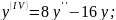

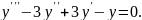
Заняття №13
Тема. Метод неозначених коефіцієнтів розв’язування неоднорідних диференціальних рівнянь n-го порядку (6 год.)
Теоретичний блок
Як зазначалось, методом варіації довільних сталих завжди можна знайти розв’язок неоднорідного лінійного рівняння у квадратурах. Даний метод дозволяє інтегрування рівняння для заданого випадку, тобто для випадку рівняння із змінними коефіцієнтами.
Проте існують певні види лінійних неоднорідних рівнянь із сталими коефіцієнтами, які дозволяють знаходження розв’язків, не застосовуючи процедуру інтегрування.
Нехай дано рівняння:
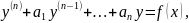
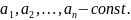
Розглянемо декілька випадків.
Якщо права частина рівняння
 є поліномом степеня n
відносно
і число 0 не є коренем характеристичного
рівняння.
є поліномом степеня n
відносно
і число 0 не є коренем характеристичного
рівняння.

Тоді частинний розв’язок шукають у формі:

де
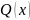 поліном того самого степеня, що і
поліном того самого степеня, що і
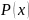 із невідомими коефіцієнтами.
із невідомими коефіцієнтами.
Підставляючи шукану формулу розв’язку у рівняння та прирівнюючи коефіцієнти біля однакових степенів, отримаємо систему рівняння для знаходження невідомих коефіцієнтів.
Загальний розв’язок рівняння записують як суму загального розв’язку відповідного однорідного рівняння і знайденого частинного.
Якщо
0 – корінь характеристичного рівняння
кратності
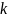 ,
тоді частинний розв’язок шукають у
формі:
,
тоді частинний розв’язок шукають у
формі:

Якщо права частина рівняння має наступний вигляд:
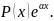
Якщо
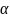 не є коренем характеристичного рівняння,
то частинний розв’язок рівняння шукаємо
у формі:
не є коренем характеристичного рівняння,
то частинний розв’язок рівняння шукаємо
у формі:
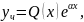
де - поліном того самого степеня, що і із невідомими коефіцієнтами.
Якщо є коренем характеристичного рівняння кратності , то частинний випадок шукаємо у формі:

Якщо права частина рівняння має вигляд:

Тоді частинний розв’язок шукають у формі:
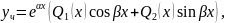
де
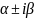 не
є коренем характеристичного рівняння;
не
є коренем характеристичного рівняння; і
і
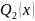 поліноми найбільшого степеня серед
поліномів
поліноми найбільшого степеня серед
поліномів
 і
і
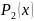 із невизначеними коефіцієнтами.
із невизначеними коефіцієнтами.
Якщо число є коренем характеристичного рівняння кратності , то частинний розв’язок шукаємо у формі:
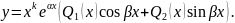
Приклад 1. Знайти розв’язок рівняння:
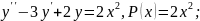

Так як 0 не є коренем характеристичного рівняння, то частинний розв’язок неоднорідного рівняння шукаємо у формі:
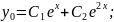

Підставимо знайдений розв’язок у вихідне рівняння.
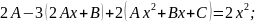
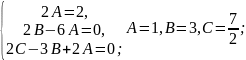
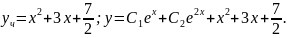
Приклад 2. Знайти розв’язок рівняння:

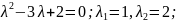
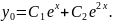
Оскільки
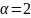 є коренем характеристичного рівняння,
то частинний розв’язок шукаємо у формі:
є коренем характеристичного рівняння,
то частинний розв’язок шукаємо у формі:
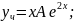
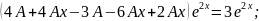
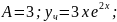

Приклад 3. Знайти розв’язок рівняння:



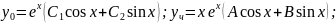
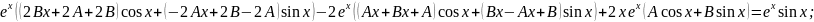
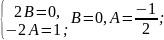

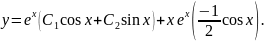
Практичний блок