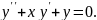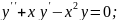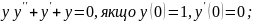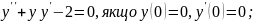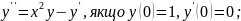50

ЗМІСТ

Заняття №9. Метод степеневих рядів……………………………………………6

Заняття №10. Неоднорідні диференціальні рівняння n-го порядку.

Метод Лагранжа (варіацій довільних сталих)…………………………………12

Самостійна робота №2…………………………………………………………..21

Заняття №11. Розв’язування однорідних диференціальних

рівнянь n-го порядку зі сталими коефіцієнтами у випадку

n дійсних різних характеристичних коренів…………………………………...22

Заняття №12. Розв’язування однорідних диференціальних

рівнянь n-го порядку зі сталими коефіцієнтами у випадку

кратних характеристичних коренів та комплексних коренів…………………26

Заняття №13. Метод неозначених коефіцієнтів розв’язування

неоднорідних диференціальних рівнянь n-го порядку………………………..31

Самостійна робота №3…………………………………………………………..46

Відповіді………………………………………………………………………….47

Література………………………………………………………………………..56

Заняття №9

Тема. Метод степеневих рядів (2 год.)

Теоретичний блок

Як відомо, інтегрування диференційних рівнянь досить рідко зводиться до квадратур. У цих випадках застосовують інші методи, найпоширенішим з яких є метод степеневих рядів.

Якщо не можна знайти загальний інтеграл диференціального рівняння

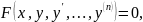
то досить часто розв’язок шукають у вигляді степеневого ряду.

Розглянемо цей метод інтегрування диференціальних рівнянь на прикладі лінійних однорідних диференціальних рівнянь другого порядку

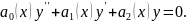
Функцію 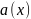називають аналітичною в околі точки 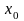, якщо її можна зобразити у вигляді степеневого ряду:

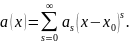
що збігається в даному колі.

Має місце наступна теорема.

Теорема. Якщо в рівнянні 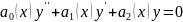функції 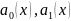та – аналітичні в околі точки 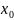і 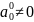, то будь-який розв’язок цього рівняння є аналітичною функцією в даному околі, тобто може бути записаний у вигляді степеневого ряду

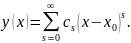
Приклад 1. Знайти загальний розв’язок диференціального рівняння

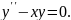
Шукатимемо розв’язок рівняння у вигляді степеневого ряду

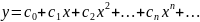
Двічі продиференціювавши даний вираз, підставимо значення 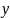та 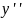у рівняння:

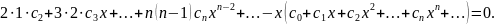
Прирівнюючи коефіцієнти при однакових степенях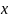 , отримуємо систему рівнянь для визначення :

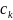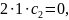
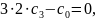
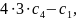
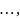
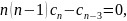
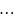
Тому

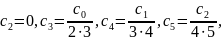
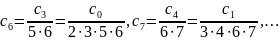
і, взагалі,

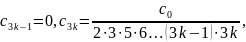
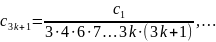
Коефіцієнти 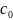і залишаються довільними. \

Тому нехай

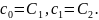
Тоді функція

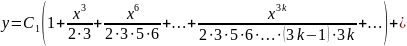
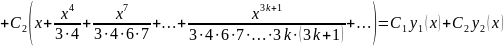
є загальним розв’язком заданого диференціального рівняння.

Приклад 2. Знайти розв’язок диференціального рівняння

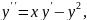
який задовольняє початкові умови

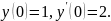
Шукатимемо розв’язок рівняння у вигляді степеневого ряду

З початкових умов випливає, що .

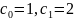Підставивши значення та даного рівняння, дістанемо

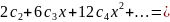
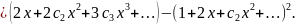
Прирівнявши коефіцієнти при однакових степенях , визначаємо :

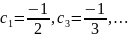
Тому шуканий розв’язок задачі Коші має вигляд

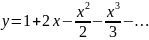
Практичний блок

1. Дано розв’язок рівняння, розв’язаного методом степеневих рядів. Заповніть пропуски.

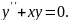
Розв’язання

Розв’язки шукаємо у вигляді ряду

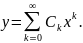
Підставляємо цей ряд у рівняння

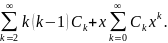
Прирівняємо до нуля коефіцієнти при у лівій частині рівняння

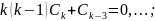
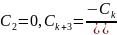
Покладемо 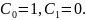Тоді відмінні від нуля будуть лише коефіцієнти

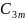
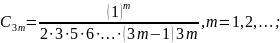
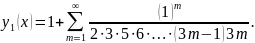
Тепер покладемо . Тоді відмінні від нуля коефіцієнти

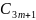
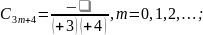
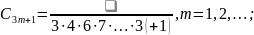
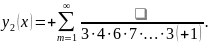
Загальний розв’язок рівняння матиме вигляд

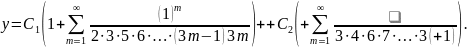
Відповідь:__________________________

2. Розв’язати рівняння методом степеневих рядів:

1. 

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Відповідь:__________________________

2. 

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Відповідь:__________________________

3. 

______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Відповідь:__________________________

4. 

______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Відповідь:__________________________

5. 

______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Відповідь:__________________________

Блок завдань для самостійного опрацювання

1. Дано розв’язок рівняння, розв’язаного методом степеневих рядів. Заповніть пропуски.