Рекомендована література

1. Башмаков М.И. Алгебра и Початки аналізу: Учеб. Для 10-11 кл. сред. шк.– М.: Просвещение, 1992.

2. Высшая математика для экономистов: Учеб. пособие для вузов/Н.Ш.Кремер и др.– М.: Банки и биржи, ЮНИТИ, 1997.

3. Мерзляк А.Г., Неміровський Д.А., Полонський В.Б. Алгебра і початки аналізу: Підруч. для 10 кл. загально-освіт. навч. закладів (академічний рівень)

4. Мерзляк А.Г., Неміровський Д.А., Полонський В.Б. Алгебра і початки аналізу: Підруч. для 11 кл. загально-освіт. навч. закладів (академічний рівень)

5. Нелін Є.П. Алгебра і початки аналізу: Підруч. для 10 кл. загально-освіт. навч. закладів (академічний рівень)

6. Нелін Є.П. Алгебра і початки аналізу: Підруч. для 11 кл. загально-освіт. навч. закладів (академічний рівень)

7. Шкиль М. И. и др. Алгебра и начала анализа. Учеб. для 11 кл. общеобр. уч.завед. – К.: ЗОДИАК ЭКО, 2003. – 400 с..

Практичне заняття №13

Тема: Поняття про первісну та її властивості

Мета: Ознайомити студентів з можливими методичними концепціями введення поняття про первісну та її властивості

Теоретичний блок

1. Провести порівняльний аналіз підходів до введення поняття про первісну в різних підручниках.

Практичний блок:

1. В завданнях вимагається знайти первісні F функцій f, що задовольняють даним умовам.

2. Вияснити, чи обов’язково первісна парної функції f є непарною. Чи може вона бути непарною? Чи обов’язково серед первісних парної функції є непарна? Дайте відповідь на ті ж запитання при умові, що функція f непе­рервна на всій числовій осі.

3. Вияснити, чи обов’язково первісна непарної функції f є парною. Чи може вона бути парною? Чи обов’язково серед первісних непарної функції є парна? Дайте відповідь на ті ж запитання при умові, що функція f непе­рервна на всій числовій осі.

4. Довести, що якщо неперервна на всій осі функція f така, що її графік має вісь симетрії х = а, то графік її первісної має центр симетрії. Доведіть, що якщо неперервна на всій осі функція f така, що її графік має центр симетрії (а; 0), то графік її первісної має вісь симетрії. З'ясуйте, чи обов'язково первісна періодичної функції f періодична. Чи може вона бути періодичною? Чи обов'язково серед первісних періодичний функції є періодична?

5. З'ясувати, чи обов'язково первісна зростаючої функції f зростаюча. Чи може вона бути зростаючою? Чи обов'язково серед первісних зростаючий функції є зростаюча?

6. З'ясувати, чи можуть визначена на всій осі функція і її первісна бути періодичними, але мати незбіжні набори періодів.

7. З'ясувати, чи може графік функції збігатися з графіком якоїсь її первісної.

8. З'ясувати, чи може графік якоїсь функції перетинатися з графіком її первісної рівно в одній точці, рівно в двох, рівно в трьох.

9. Знайти усі значення параметра а, такі, що первісна функції

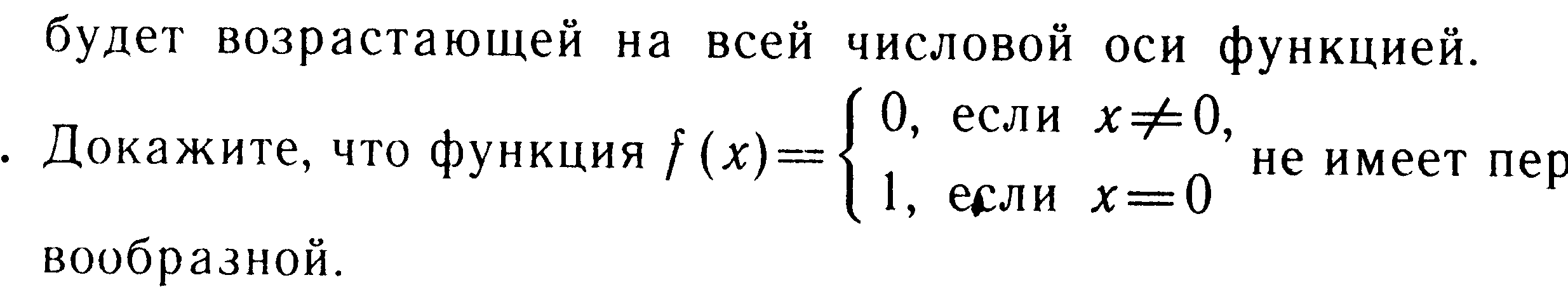
10. В завданнях вимагається знайти всі функції f, що задовольняють даним умовам.

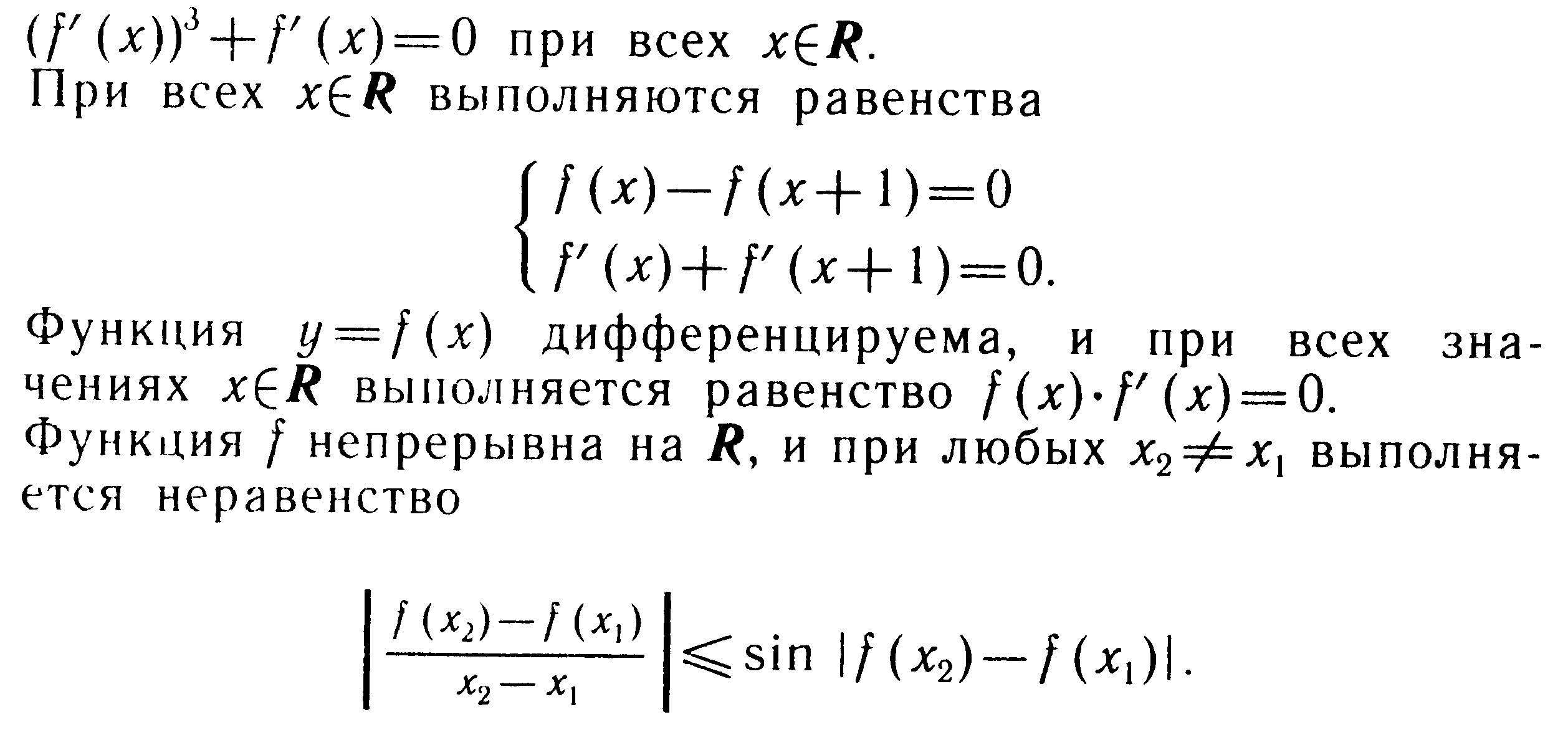
Практичне заняття № 14

Тема: Поняття про визначений інтеграл та його обчислення. Найпростіші диференціальні рівняння.

Мета: Ознайомити студентів з можливими методичними концепціями введення поняття про визначений інтеграл та найпростіші диференціальні рівняння.

Теоретичний блок

1. Провести порівняльний аналіз підходів до введення поняття про визначений інтеграл у різних підручниках.

2. Описати методику ознайомлення учнів з найпростішими диференціальними рівняннями.

Практичний блок:

1. Описати методику роботи над задачами з підручника 11 класу №№ 63 (10-22), 64 (13-16), 65, 66, 68.

2. Описати методику роботи над задачами із збірника для державної атестації №№ 802-815.