Практичне заняття № 8 Контрольна робота №1

Оцінювання контрольної роботи проводиться шляхом підсумовування балів, отриманих за виконання кожного завдання, які в свою чергу є сумою балів, виставлених за такими критеріями

№ завдання	№. критерію	Критерій	Кількість балів
1.	1.1	Правильність
	1.2	Повнота
	1.3	Обґрунтованість методичних концепцій
	1.4	Використання різних підходів

Максимальна кількість балів за кожне завдання – 2 бали (за всю контрольну роботу – 6 балів). Якщо результат виконання завдання задовольняє певному критерію, то студент отримує 1 бал.

Практичне заняття № 9

Тема: Поняття про границю та неперервність функції.

Мета: Ознайомити студентів з можливими методичними концепціями введення понять про границю та неперервність функції.

Теоретичний блок

1. Опрацювати відповідний матеріал з підручника М.І.Шкіль та ін., проаналізувати основні алгоритми та систему вправ.

Практичний блок:

1. Описати методику роботи над задачами:

1)

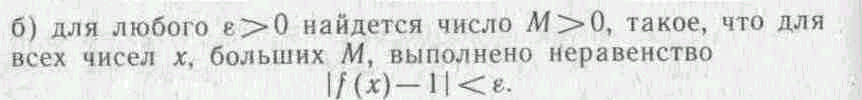
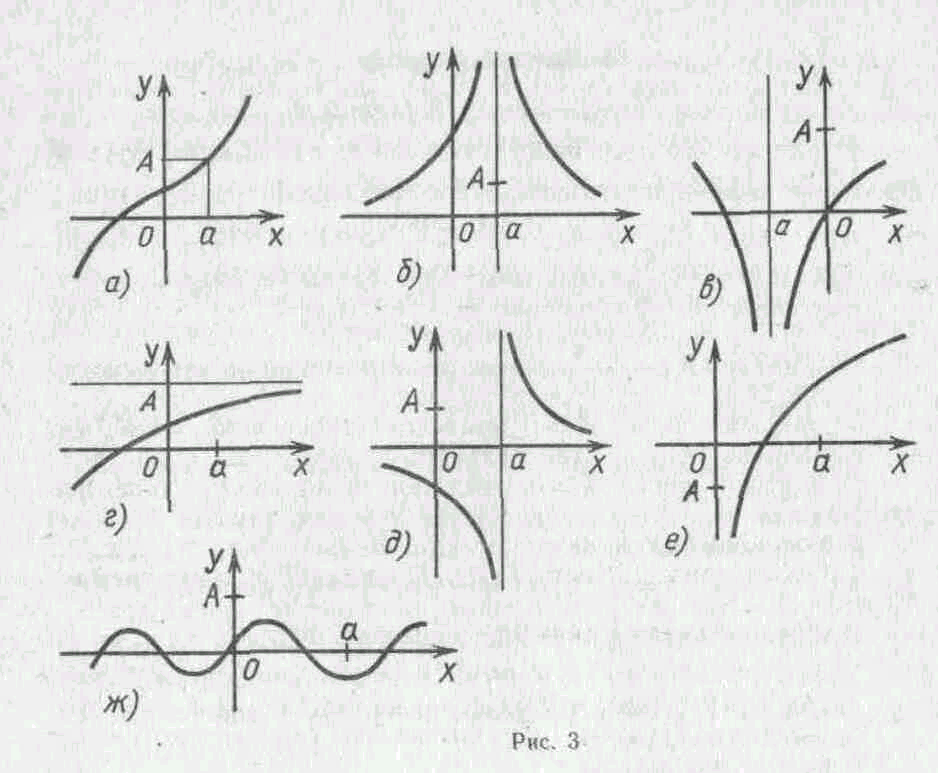
2) На рисунке 3 изображены графики функции, отмечены чис­ла а и А. Укажите, для каких функций справедливы следу­ющие утверждения:

5) Приведите, если это возможно, примеры функций f и g, таких, что выполнены следующие утверждения (если это невозможно, объясните почему

Практичне заняття №10-11 Тема: Похідна та її використання

Мета: Ознайомитись з методикою введення, знаходження і використання похідної до дослідження функцій.

Теоретичний блок

1. Описати можливі напрями пропедевтики введення поняття похідної.

2. Сформулювати алгоритм знаходження похідної функції у точці, навести приклади використання.

3. Охарактеризувати метод доведення правил диференціювання.

4. Провести порівняльний аналіз різних методичних концепцій введення та обґрунтування достатньої ознаки зростання та спадання функції, питань, пов’язаних з екстремумами функції.

Практичний блок:

1. Описати методику роботи над задачами

1. Дослідити дані функції на диференційованість:

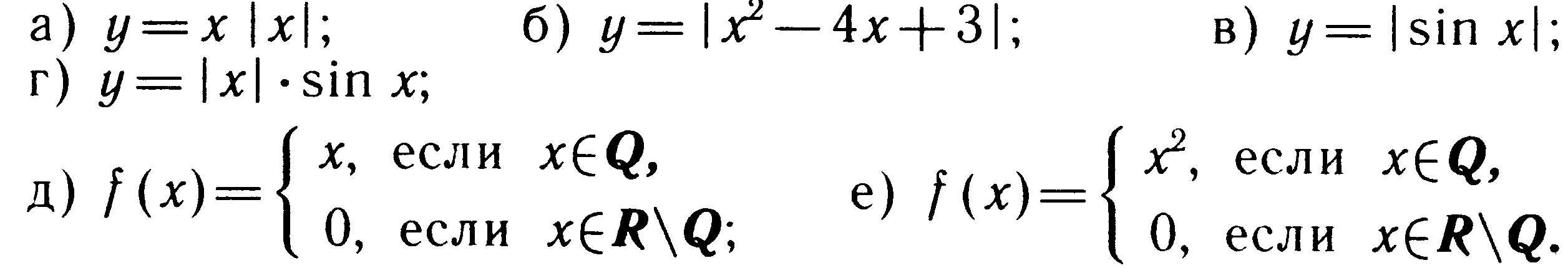
2. Наведіть, якщо це можливо, приклади функцій f і g, що задовольняють даним умовам (якщо це неможливо, поясніть чому):

3. Довести наступні твердження:

а) похідна непарної функції – парна функція;

б) похідна парної функції – непарна функція;

в) похідна періодичної функції – періодична функція.

4) Знайти область значень функції

5) Вияснити, скільки коренів має рівняння

Практичне заняття № 12 Тема: Використання похідної до розв’язання рівнянь і нерівностей, у фізиці, техніці та економіці.

Мета: Ознайомити студентів методикою використання похідної до розв’язання рівнянь і нерівностей, у фізиці, техніці та економіці.

Теоретичний блок

Практичний блок:

1. Використовуючи літературу, підготувати повідомлення (на 10-15 хв), підібрати відповідні приклади по одному із запропонованих питань

1. Використання похідної у фізиці та техніці.

2. Розв’язання мінімаксних задач.

3. Використання похідної в економіці.

4. Використання похідної для розв’язання рівнянь та нерівностей.