3.2 Граф-схема алгоритма

Составим структуру работы логической схемы. Ниже приведена блок–схема

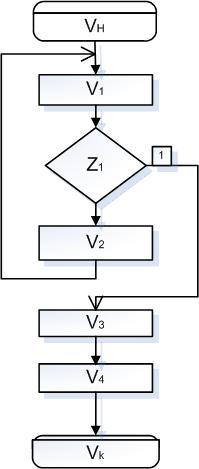
Рисунок 3.1 – Блок–схема логического устройства

Опание машинных процедур

Procedure Stuck(S1, S2: Diz; IndexS1, IndexS2 : byte);

Данная процедура склеивает два, передаваемых ей дизъюнкта. Дизъюнкты задаются в параметрах S1, S2. Индексы IndexS1, IndexS2 определяют индексы этих дизъюнктов в главном рабочем массиве . Алгоритм работы процедуры следующий: сначала ищется количество склеивающихся символов. Если их 0, то они одинаковые, и в конечный массив записывается только один из них. Если 1, то определяется местоположение символа, по которому данные две дизъюнкции склеиваются, и заменяем этот символ на ‘*’. Все полученные результаты заносятся в массив REZ.

Все остальные функции и процедуры программы связаны с действиями над массивами, то есть не имеют непосредственного отношения к данному методу нахождения МДНФ. Поэтому нет смысла их описывать [13].

Заключение

В данной курсовой работе были рассмотрены методы минимизации: методы Квайна, Квайна-Маккласки, карт Карно, неопределенных коэффициентов, а также рассмотрено прямое алгебраическое преобразование. Для двух из них (метода неопределенных коэффициентов и метода Квайна) были разработаны программы. При этом особенно трудно было реализовать процедуры, отвечающие за логические операции. Причем просматривалась следующая закономерность: чем легче был метод для ручного исполнения, тем труднее было написать для него программу. Взять хотя бы метод карт Карно. С его помощью вручную очень легко получить МДНФ, составить таблицу и выбрав правильные прямоугольники. Но если взяться за реализацию этого метода программно, то сразу возникают трудности, особенно при написании процедуры выбора правильных прямоугольников. Это будет очень сложная логическая процедура, кажется, что все просто.

Иначе выглядит метод неопределенных коэффициентов. Для машинной реализации он подходит больше других, так как в нем мы имеем дело с массивами, для работы с которыми не надо особо сложной логики. И конечно ручное исполнение этого метода крайне нерационально, так как приходиться решать систему из 16-ти уравнений. Это для четырех переменных, а для пяти это будет 32 уравнения. Такой метод для ручного исполнения не подходит.

В задаче курсовой работы также входил синтез логической схемы. Полученная схема МДНФ была реализована в трех базисах: Буля, Пирса, Шеффера. Анализ и оценка аппаратурных затрат также приведена в данной записке.

Список использованных источников

1. Влах, Кишор, Сингхал “Машинные методы анализа и проектирования электронных схем.” Москва, изд. “Радио и связь”, 1988г.

2.“Измерения параметров цифровых интегральных микросхем.” (под ред. Эйдукаса Д.Ю., Орлова Б.В.) Москва, “Радио и связь”, 1982г.

3. Кузнецов О. П., Адельсон-Вельский Г. М. Дискретная математика для инженера. – М.: «Энергия», 1980. — 344 с.

4. Лазер И.М., Шубарев В.А. “Устойчивость цифровых микроэлектронных устройств.” Москва, “Радио и связь”, 1983г.

5. Марченков С. С. Замкнутые классы булевых функций. — М.: Физматлит, 2000.

6. Нефедов А.В., Савченко А.М., Феоктистов Ю.Ф.“Зарубежные интегральные микросхемы для электронной аппаратуры.” Москва, Энергоатомиздат, 1989г.

7.Ногов Ю.Р.“Математические модели элементов интегральной электроники.” Москва, “Современное радио”, 1976г.

8. Пухальский Г.И., Новосельцева Т.Я. “Цифровые устройства.” Санкт-Петербург, изд. “Политехника”1996г.

9. Самофалов К.Г, Романкевич А.М. Прикладная теория цифровых автоматов. – Киев “Вища школа”,1987

10. Схрейвер А. Теория линейного и целочисленного программирования. – М.: Мир, 1991 

11.Сысоев В.В.“Структурные и алгоритмические модели автоматизированного проектирования производства изделий электронной техники. ”Воронеж, Воронежский технологический институт, 1993г.

12. Токхейм Р.“Основы цифровой электроники” Москва, изд. “Мир”, 1988г.

13.Чахмахсазян Е.А., Мозговой Г.П., “Математическое моделирование и макромоделирование биполярных элементов электронных схем.”Москва, “Радио и связь”, 1985г.

14. Шило В.Л. “Популярные цифровые микросхемы.”Москва, Металлургия, 1988г.

15. Яблонский С. В. Введение в дискретную математику. — М.: Наука, 1986.

Размещено на Allbest.ru