2.4 Метод диаграмм Вейча
Рассмотрим один из алгоритмов минимизации, предложенный американский ученым Вейчем. Вейч предложил специальные диаграммы-карты, в которые можно записать все конституенты единицы, входящие в СДНФ (конституенты нуля, входящие в СКНФ) той или иной булевой функции. На рисунке 2.11 в качестве примера приведены диаграммы для минимизаций функций двух, трех и четырех переменных соответственно.
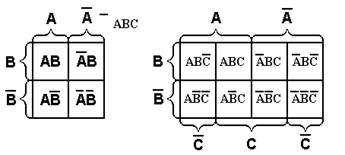
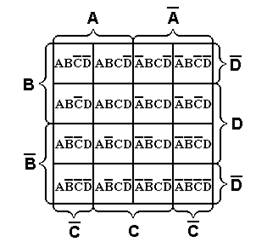
Рис. 2.11 – Диаграммы Вейча для функций 2-х, 3-х и 4-х переменных.
Каждой клетке диаграммы в случае минимизации СДНФ соответствует определенная конституента единицы. Метод минимизации с помощью диаграмм Вейча заключается в следующем. Конституенты единицы, входящие в СДНФ булевой функции, заносятся в соответствующие клетки диаграммы. Удобно наличие соответствующей конституенты единицы изображать в клетке диаграммы цифрой 1, а отсутствие – 0. Все диаграммы построены таким образом, что рядом расположенные единицы по горизонтали или вертикали склеиваются между собой в соответствии с законом склеивания алгебры логики. Одну и ту же конституенту единицы можно использовать для склеивания с несколькими другими конституентами единицы с целью получения наиболее простого окончательного выражения. Цель всех операций – получить как можно меньшее число прямоугольников (в том числе квадратов), чтобы число членов СДНФ уменьшилось, получив в итоге МДНФ. булевая функция минимизация карно
Формировать прямоугольники можно только при включении в них хотя бы одного нового осуществлять и путем замыкания крайних ребер в «бочку». Таким образом, полученная диаграмма Вейча геометрически образует цилиндр. На рисунке 2.12 приведены некоторые правила склеивания конституент единицы для функций 2-х и 3-х переменных.
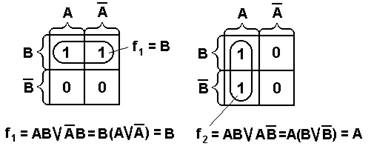
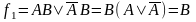
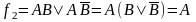
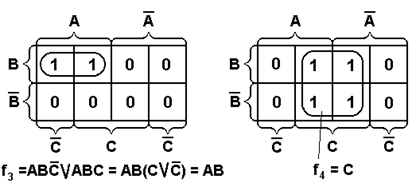
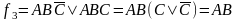
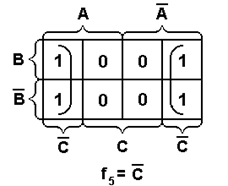
Рисунок 2.12 – Примеры для иллюстрации правил склеивания.
Метод минимизации СДНФ с помощью диаграмм Вейча включает в себя следующие шаги:
1. производится занесение в соответствующую диаграмму конституент единицы, входящих в СДНФ минимизируемой функции;
2. используя приведенные выше правила склеивания, находят простые импликанты функций (простой импликантой называется некоторая конъюнкция, полученная в результате склеивания конституент единицы, не участвующая в склеивании ни с одной другой из конъюнкций);
3. находится искомая минимальная дизъюнктивная нормальная форма (МДНФ) ФАЛ выбором минимальной совокупности простых импликант, покрывающей все конституенты единицы диаграммы.
В
качестве примера найдем МДНФ функции.
Диаграмма Вейча этой функции представлена
на рисeyrt
2.13. Из рисунка видно, что в результате
склеивания образовались две простые
импликанты: BC и
.
Импликанта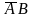 
участвует
в склеивании с конъюнкциями: BC и
и
поэтому не является простой. Таким
образом, полученная вид f=BC
.
В истинности полученного выражения
можно убедиться путем подстановки всех
наборов переменных А,
В и
С.
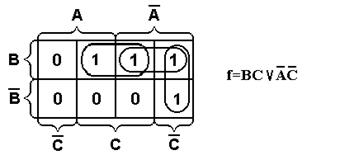
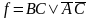
Рисунок 2.13 – Пример минимизации функции
Аналогом
диаграмм Вейча являются карты
Карно.
Они позволяют изображать на плоскости
прямоугольника конституенты единицы
(нуля) более четырех переменных. В отличие
от диаграмм Вейча, в которых отдельным
строкам и столбцам соответствуют
отдельные переменные, в картах Карно
им можно присваивать значения нескольких
переменных. При этом должны быть
представлены все возможные комбинации
этих переменных, например: AB,
,
и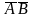 
.
Таким образом, общее количество переменных
минимизируемой с помощью карты Карно
может быть больше, чем в случае
использования диаграмм Вейча. Сам
процесс минимизации аналогичен описанному
на примере диаграмм Вейча [8].