Введение

Очень часто приходится реализовывать совокупности булевых функций.

Традиционно булевы функции используются в качестве математических моделей цифровых устройств. Процедура минимизации булевых функций, как правило, применяется на этапе логического синтеза для получения экономичного представления проектируемого устройства.

Если произвести минимизацию булевых функций, входящих в систему независимо друг от друга, то общая схема будет состоять из изолированных подсхем. Её можно иногда упростить за счет объединения участков подсхем, реализующих одинаковые члены, входящие в несколько булевых функций системы. Задача минимизации систем булевых функций хорошо исследована в классе функционально полных систем: «дизъюнкция», «конъюнкция», «отрицание».

Целью данной работы является рассмотрение алгоритмов минимизации булевых функций: Метод Квайна, Метод карт Карно, Метод Квайна и Мак–Класки, Метод диаграмм Вейча, Метод неопределенных коэффициентов.

1. Представление булевых функций

Используя законы булевой алгебры, можно получить для одной и той же логической функции множество эквивалентных представлений. Чем проще выражение функции, тем экономичнее ее практическая реализация на интегральных микросхемах. Сложность булевой функции определяется ее рангом, т.е. количеством переменных в ее конъюнктивных или дизъюнктивных членах. Пусть I = {0, 1} – множество, состоящее из двух элементов: 0 (ложь) и 1 (истина). Булевой функцией f : In ®I называется произвольная функция f(x1, x2, …, xn) от n аргументов, принимающая значения в I. Будем предполагать, что функции от n переменных определены для всех натуральных чисел n ³ 0, причем функциями от 0 переменных являются константы 0 и 1.

Представление булевой функции в СовДНФ (совершено дизъюнктивной нормальной форме) в большинстве случаев не является минимальным.

Используя операции поглощения и склеивания, её можно существенно упростить. Часто используется неполное склеивание, при котором оба члена, участвовавших в склеивании (или один из них), могут повторно склеиваться с другими оставшимися членами Сов ДНФ.

В процессе минимизации важно отыскать смежные конституенты, которые отличаются только одним аргументом (в одну конституенту аргумент входит с инверсией, а в другую – без нее).

Конституентой единицы (коньюнктивным термом) называется функция f(x1,x2,...,xn), принимающая значение 1 только на единственном наборе.

Конституента единицы записывается как логическое произведение n различных булевых переменных, некоторые из них могут быть с отрицаниями. Можно легко выразить любую булеву функцию как дизъюнкцию конституент единицы, соответствующих тем наборам, на которых функция равна 1.

Две смежные конституенты, склеиваясь, образуют импликанту рангом на единицу ниже, чем исходные конституенты[3].

Используя, например, неполное склеивание последней коституенты в СовДНФ функции F1 последовательно с остальными, приходим к следующему выражению 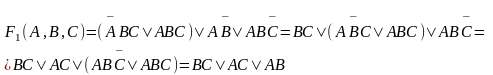(1):

(1)

Процесс многоступенчатого склеивания приводит к импликантам, которые не склеиваются с другими, такие импликанты называют простыми. Форма записи булевой функции в ДНФ, состоящая только из простых импликант, называется сокращенной дизъюнктивной нормальной формой (СокрДНФ).

В некоторых случаях в СокрДНФ могут содержаться лишние импликанты, которые могут быть исключены без изменения значения функции.

Одним из методов отыскания лишних импликант является метод испытания членов: чтобы испытать некоторый член функции, следует исключить его из СокрДНФ и подставить в оставшееся выражение такие значения аргументов, которые обращают исключенный член в единицу. Если при такой подстановке оставшееся выражение окажется тождественно равным единице, то испытуемый член является лишним[9].

Найдем для примера тупиковую форму СокрДНФ 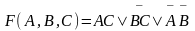(2)

Испытаем член AC. AC = 1, если A = 1 и C = 1. Подставим в оставшееся выражение 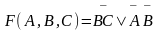 A = 1 и C = 1, получим

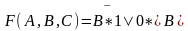
При B = 0 F(A, B, C) = 1·1 B 0·0 = 1, но при B=1 F(A, B, C) = 0·1 B 0·0 = 0. Следовательно, член AC не лишний.

Испытаем член BC, равный 1 при B = 0, C = 1. При этом выражение 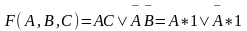(3)

(3)

Последнее выражение равно 1 как при A = 1, так и при A = 0. Поэтому член 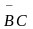 – лишний.

Испытание члена 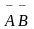 по этой же методике показывает, что он не является лишним, в итоге тупиковая форма исходной функции имеет вид 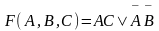(4):

(4)

Способы представления булевых функций

Результат выполнения логических операций над двоичными переменными А, В, С, ... также представляет собой двоичную переменную F, которую называют булевой функцией. Наиболее распространены следующие способы представления булевых функций[5].

Табличный способ. При этом способе функция представляется в виде таблицы истинности, в которую вписываются все возможные наборы аргументов (А, В) и для каждого набора устанавливается значение функции F = 0 или F =1.

Таблица 1.1 – Таблица истинности

A	B	F
0	0	0
0	1	1
1	0	1
1	1	0

Алгебраический способ. Существует две формы представления функций в алгебраическом виде:

ДНФ – дизъюнктивная нормальная форма, представляет собой логическую сумму элементарных логических произведений, в каждое из которых аргумент или его отрицание входят не более раза. Например выражение (5):

F(A, B, C) = AB + AC + 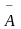 BC (5)

СДНФ – совершенно ДНФ (каждое слагаемое содержит все переменные или их отрицания). Например выражение (6):

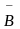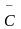F(A, B, C) = ABC + A C + AB . (6)

КНФ – конъюнктивная нормальная форма, представляет собой логическое произведение элементарных логических сумм. Например выражение(7):

F(A, B, C) = (A + B)(A +  + C) (7)

СКНФ – совершенная конъюнктивная нормальная форма (каждая сумма содержит все переменные или их отрицания). Например выражение (8):

F(A, B, C) = (A +   + )(  + B + ). (8)

На основе полученной формулы строят комбинационную схему, состоящую из логических элементов И, ИЛИ, НЕ. Логические элементы, предназначенные для выполнения указанных в формуле операций, располагаются в схеме, начиная от входов, в том же порядке, в котором выполняются логические операции.

Процесс синтеза логических цепей обычно проводят в следующей последовательности. Вначале составляют таблицу функционирования логической цепи. Затем записывается логическая функция, которая после минимизации преобразуется к виду, удобному для реализации на логических элементах заданного типа[2].