Хід роботи
І. Постановка задачі.
Задача
№ 1
Квазілінійнаі
регресія в загальному вигляді описана
рівнянням
.
На основі статистичних даних фактора
x
і показника y
N |
x |
у |
1 |
1,01 |
12,03 |
2 |
1,51 |
8,84 |
3 |
2,02 |
6,99 |
4 |
2,51 |
6,03 |
5 |
3,01 |
5,55 |
6 |
3,49 |
5,12 |
7 |
3,98 |
4,63 |
8 |
4,48 |
4,41 |
9 |
4,99 |
4,01 |
10 |
5,49 |
3,96 |
11 |
5,97 |
3,70 |
12 |
6,47 |
3,75 |
13 |
6,98 |
3,72 |
14 |
7,51 |
3,53 |
15 |
7,99 |
3,25 |
хр |
6,45 |
|
Знайти оцінки:
параметрів кривої зростання , ; (перевірити знайдені значення параметрів за допомогою матриць)
коефіцієнта кореляції
.
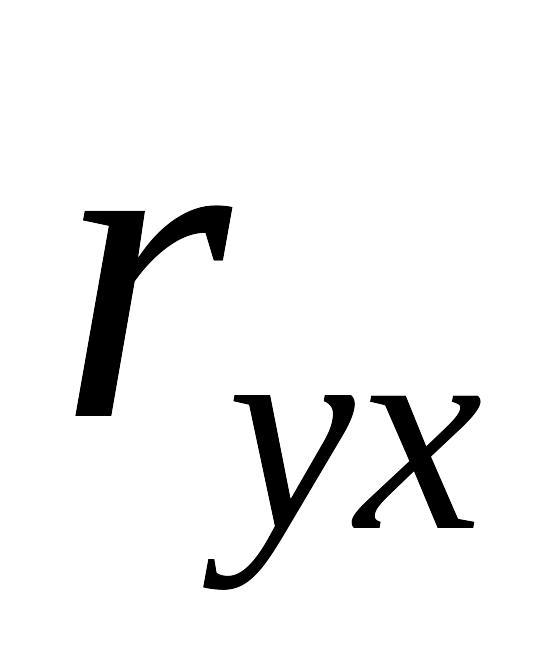2. Використовуючи
критерій Фішера, з надійністю
=0,05
оцінити адекватність прийнятої моделі
статистичним даним.
3. Якщо модель адекватна статистичним даним, то знайти:
з надійністю =0,05 надійні зони базисних даних;
прогноз показника та його надійні інтервали;
коефіцієнт еластичності для базисних даних і прогнозу.
4. Побудувати графіки:
статистичних даних;
кривої зростання і її довірчої зони;
коефіцієнта еластичності.
Порядок виконання роботи
Запустіть програму EXCEL. Згідно з даними діапазону (х, у), занесемо початкові значення фактора x, значення показника y, та прогнозне значення фактора xр.
Приведемо залежність до лінійного виду, ввівши заміну
:
Знайдемо параметри i
за допомогою МНК за формулами з
урахуванням введеної заміни виду:
, або
(
)
.
Для цього необхідно підрахувати
добутки
та
і відповідні суми.
Кількість значень факторів n=15
Перевірити знайдені значення параметрів за допомогою матриць
Для знаходження розрахункових значень показника
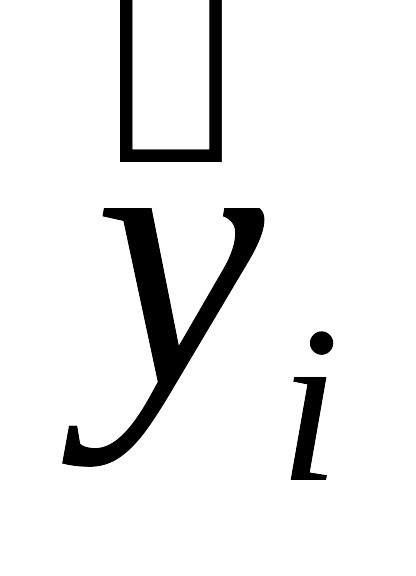використовується рівняння регресії:
при правильному виконанні
розрахунків
,
Зробити оцінку адекватності моделі
Для оцінки коефіцієнта кореляції будемо використовувати статистичну функцію CORREL(блок значень Z; блок значень Y), або
.
Знайти
Для оцінки адекватності прийнятої моделі використовують критерій Фішера, розрахункове значення якого знаходять за формулою:
,
або
,
де
Табличне значення Fкр знаходимо за допомогою статистичної функції FINV( ;m;n-k)(FINV(0,05;1;13))
Якщо
>
Fкр,
то з надійністю Р
можна вважати, що прийнята модель
адекватна експериментальним даним
Знайти надійну зону базисних даних
Обчислимо значення функції Ст’юдента
за допомогою статистичної функції
TINV(
;n-k)
(TINV(0,05;13))Дослідити значущість коефіцієнта кореляції:
Знайдемо оцінку середньоквадратичного відхилення помилок -
:
Підібране
лінійне рівняння зазнає впливу помилок,
тому базисні значення
змінюються в деяких межах. Надійні межі
базисних середніх значень показника
визначаються за формулою:
,
Знаходимо значення
.Знаходимо значення
та значення
за формулами:
, 
Знаходимо коефіцієнт еластичності за формулою:
,
для
нашого випадку:
або за формулою даною в таблиці
5.1(відповідно до функції)
Він показує, на скільки відсотків зміниться показник y, якщо фактор x зміниться на 1%
Знайти значення прогнозу показника
р.Для прогнозного значення визначимо: значення
,
,
,
,
,
.Для наочного уявлення результатів будуємо графіки:
статистичних даних z i y;
кривої зростання ;
довірчої зони , ;
коефіцієнта еластичності
.
Проаналізувати отримані графіки. Підвести підсумки лабораторної роботи і зробити висновки.
ІІ. Завдання для самостійної роботи.
(Для визначення числових значень коефіцієнтів використовується: n – Ваш порядковий номер в списку студентів групи, k – остання цифра номеру Вашої групи).
1. Розв’язати задачу 1 для регресії нелінійної за показником відповідно до свого варіанту (вид функції визначає викладач)
2. Розв’язати задачу 2(дані таблиці 5.2) для регресії, нелінійної за показником відповідно до свого варіанту (вид функції визначає викладач)
Таблиця 5.2
Значення фактора
Xi |
|
|
|
|
|
|
|
|
|
|
|
1 |
1,01 |
9,35 |
9,33 |
1,15 |
1,01 |
1,08 |
1,10 |
1,02 |
0,32 |
0,11 |
1,03 |
2 |
1,51 |
15,26 |
15,72 |
1,64 |
1,35 |
1,53 |
1,33 |
1,59 |
0,93 |
0,39 |
1,63 |
3 |
2,02 |
20,67 |
20,87 |
2,28 |
1,71 |
2,05 |
1,58 |
2,12 |
1,59 |
0,66 |
2,16 |
4 |
2,51 |
26,49 |
26,74 |
2,77 |
2,09 |
2,58 |
1,81 |
2,61 |
2,29 |
0,89 |
2,71 |
5 |
3,01 |
33,14 |
31,95 |
3,42 |
2,49 |
3,02 |
2,09 |
3,05 |
2,92 |
1,15 |
3,26 |
6 |
3,49 |
39,39 |
37,97 |
3,78 |
2,85 |
3,58 |
2,32 |
3,56 |
3,62 |
1,43 |
3,77 |
7 |
3,98 |
44,49 |
44,61 |
4,49 |
3,28 |
4,06 |
2,59 |
4,00 |
4,30 |
1,67 |
4,35 |
8 |
4,48 |
50,71 |
51,32 |
5,08 |
3,64 |
4,56 |
2,85 |
4,50 |
4,99 |
1,95 |
4,91 |
9 |
4,99 |
56,01 |
58,23 |
5,63 |
4,04 |
5,01 |
3,14 |
5,03 |
5,63 |
2,23 |
5,50 |
10 |
5,49 |
63,00 |
64,57 |
6,11 |
4,47 |
5,51 |
3,43 |
5,56 |
6,25 |
2,45 |
6,01 |
11 |
5,97 |
68,79 |
71,32 |
6,79 |
4,83 |
6,06 |
3,69 |
6,04 |
6,90 |
2,72 |
6,60 |
12 |
6,47 |
74,97 |
77,53 |
7,39 |
5,20 |
6,52 |
3,90 |
6,50 |
7,56 |
2,93 |
7,20 |
13 |
6,98 |
81,39 |
84,35 |
7,84 |
5,70 |
7,02 |
4,20 |
7,01 |
8,21 |
3,13 |
7,78 |
14 |
7,51 |
87,91 |
90,87 |
8,48 |
6,02 |
7,53 |
4,42 |
7,58 |
8,91 |
3,41 |
8,35 |
X15 |
7,99 |
93,94 |
96,33 |
8,57 |
6,52 |
8,05 |
4,72 |
8,04 |
9,57 |
3,63 |
8,90 |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
Хn |
7,99+2/N |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
хр |
8,45 |
100,15 |
102,68 |
9,46 |
6,90 |
8,48 |
4,99 |
8,52 |
10,20 |
3,85 |
9,42 |
Розрахувати Хn ( останнє значення діапазону [X1-Xn]): Х15+2/N, кількість вузлів між останнім Х15 і Хн дорівнює N(номер варіанту)
Таблиця 5.3
Значення показника
Yi |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
1 |
12,03 |
8,68 |
9,67 |
5,44 |
5,02 |
4,37 |
2,72 |
3,02 |
5,71 |
1,78 |
1,27 |
2 |
8,84 |
9,86 |
11,82 |
7,01 |
5,51 |
4,01 |
2,91 |
2,94 |
5,97 |
2,22 |
1,42 |
3 |
6,99 |
10,65 |
13,76 |
10,62 |
6,52 |
3,29 |
3,18 |
2,71 |
3,82 |
4,30 |
1,93 |
4 |
6,03 |
11,20 |
13,48 |
13,40 |
7,92 |
3,10 |
3,50 |
3,32 |
3,27 |
5,49 |
2,35 |
5 |
5,55 |
11,87 |
14,99 |
17,42 |
9,64 |
3,22 |
3,71 |
2,69 |
3,06 |
6,57 |
2,73 |
6 |
5,12 |
12,32 |
16,74 |
21,70 |
10,06 |
2,99 |
3,88 |
2,99 |
2,86 |
7,15 |
3,93 |
7 |
4,63 |
12,59 |
16,41 |
28,60 |
14,06 |
2,90 |
4,06 |
3,22 |
2,79 |
10,48 |
5,12 |
8 |
4,41 |
12,85 |
17,88 |
35,68 |
19,17 |
2,37 |
4,18 |
3,42 |
2,63 |
12,52 |
6,55 |
9 |
4,01 |
13,18 |
19,88 |
41,37 |
25,58 |
1,87 |
4,39 |
4,00 |
2,54 |
17,53 |
9,05 |
10 |
3,96 |
13,40 |
20,50 |
49,45 |
32,56 |
1,82 |
4,44 |
3,43 |
2,60 |
24,23 |
12,24 |
11 |
3,70 |
13,71 |
20,01 |
60,03 |
37,02 |
1,89 |
4,55 |
4,49 |
2,41 |
31,95 |
17,28 |
12 |
3,75 |
13,91 |
22,26 |
68,90 |
47,97 |
2,28 |
4,63 |
4,44 |
2,47 |
41,65 |
25,25 |
13 |
3,72 |
14,11 |
22,31 |
76,80 |
61,09 |
1,46 |
4,61 |
4,83 |
2,41 |
52,00 |
36,19 |
14 |
3,53 |
14,20 |
23,34 |
89,84 |
70,61 |
1,56 |
4,66 |
4,62 |
2,50 |
73,81 |
52,81 |
Y15 |
3,25 |
14,38 |
22,68 |
92,49 |
88,60 |
1,73 |
4,66 |
5,01 |
2,45 |
95,47 |
76,20 |
Yi |
3,25-3,25*0,0N |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
Уn |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
Розрахувати Уi ( кожне значення діапазону [У1-Уn]): Уі=Уі±Уі*0,0N(номер варіанту). ± залежить від того зростає чи спадає діапазон значень [У1-Уn]