Контрольні питання.

1. Виконати короткий огляд теоретичних і практичних результатів побудови міжгалузевих балансів.

2. Охарактеризувати квадранти міжгалузевого балансу виробництва і розподілу продукції у народному господарстві.

3. Розкрити економічний зміст міжгалузевих матеріальних потоків, коефіцієнтів прямих і повних витрат.

4. Записати і пояснити основні математичні залежності матричної економічної моделі.

5. Пояснити суть коефіцієнтів прямих матеріальних витрат.

6. Пояснити методику обчислення коефіцієнтів повних витрат.

7. Пояснити обчислення прямої і повної трудомісткості продукції.

8. Пояснити обчислення показників прямої і повної фондомісткості продукції.

9. Дати характеристику динамічної моделі міжгалузевого балансу. Її переваги і недоліки.

10. Розкрити проблеми оптимізації міжгалузевого балансу, навести приклад оптимізаційної моделі.

11. Пояснити використання матричних моделей в економічному аналізі.

12. Пояснити методику оцінки продукції у вартісному міжгалузевому балансі.

13. Пояснити особливості методик визначення коефіцієнтів прямих матеріальних затрат.

14. Пояснити методику визначення обсягів і кінцевої продукції в міжгалузевому балансі.

Лабораторна робота 3-4 Побудова лінійної економетричної моделі. (ч.1) Дослідження адекватності лінійної економетричної моделі. (ч.2)

Мета: набуття навиків побудови та аналізу однофакторних регресійних моделей

Теоретичні відомості

Задача, з якою стикається кожний, хто вивчає економіку — це задача про встановлення взаємозв’язків між економічними величинами. Так, попит на деякий товар, що формується на ринку, залежить від ціни товару та ціни конкуруючих товарів, споживчого доходу і т.д. Витрати, що пов’язані з виготовленням будь-якої продукції, залежать від обсягу виробництва, технології, умов, від цін на основні виробничі ресурси.

Цю проблему економіки можна вирішити, побудувавши економетричну модель. Економетрична модель — це функція чи система функцій, що описує кореляційнорегресійний зв’язок між економічними показниками, один чи кілька з яких є залежною змінною, інші — незалежними.

У загальному вигляді економетрична модель запишеться так:

y= f(x₁,x₂,x₃..x_m,u),

де y — залежна змінна; x_j,(j =1,m) — незалежні змінні; u — стохастична складова.

Найпростішою формою залежності є лінійна залежність між двома змінними, що математично описується так:

y=ах+b+u

В даній лабораторній роботі ми будемо працювати з таким видом залежності.

Хід роботи

І. Постановка задачі

Задача № 1 Кожному не раз доводилося стояти в довгих чергах в супермаркетах. Деякі магазини через неоптимальну роботу кас втрачають своїх клієнтів. На перший погляд, все залежить від кількості клієнтів, які підходять до кас, але насправді основним тут є кількість товарів, які знаходяться в кошиках клієнтів. Дослідимо залежність часу обслуговування клієнта в супермаркеті від кількості товарів в його кошику.

Таблиця даних містить результати замірювання часу обслуговування клієнтів в супермаркеті та число товарів в їхніх кошиках.

K - остання цифра номеру групи; N - номер студента по списку.

Кількість товарів в покупці (X)	Час обслуговування на касі, секунд (Y)	Кількість товарів в покупці (X)	Час обслуговування на касі, секунд (Y)
10	56	1	20
6	65	7	29
10	55	16	79
41+K	152-N	1	12
1	32	22	135
52+K	152-N	7	35
9	66	9	65
20	305	12	88
23	106	3	50
3	27	38+K	181-N
1	30	6	50
1	55	1	39
7	149	9	46
39	238	12	82
13	60	16	129
28	95	12	74
1	23	3	53
42+K	143-N	4	52

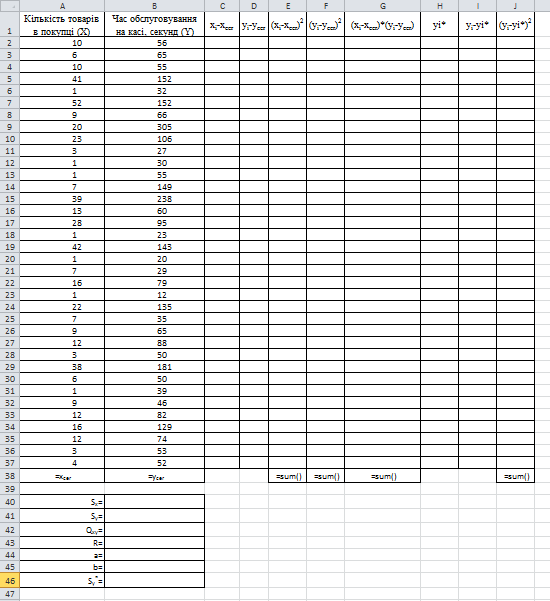
• Побудувати таблицю-форму для введення проміжних результатів(таб.1)

Оскільки залежність між змінними х, у описується лінійною залежністю виду у= ах+b, знайдемо коефіцієнти а та b.

• Обчислюємо середні значення досліджуваних величин:

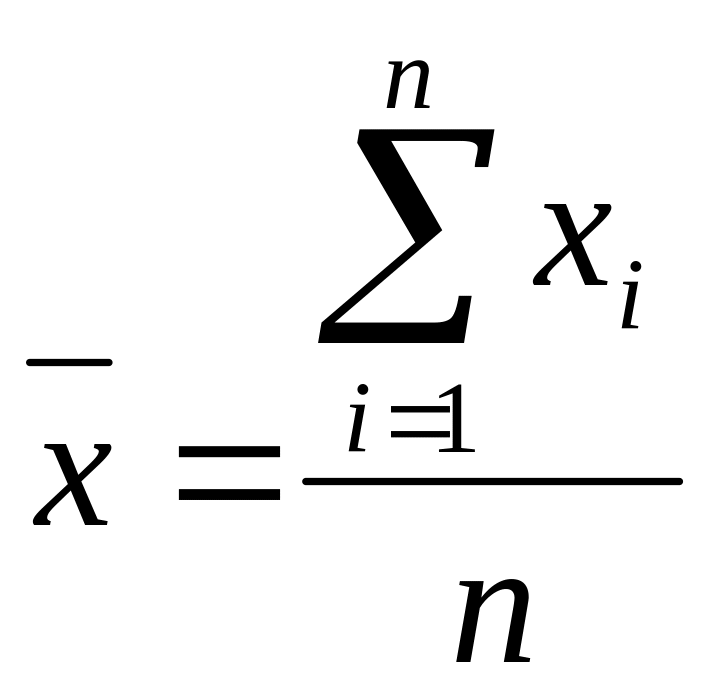
• Знаходимо середнє квадратичне відхилення:

Таблиця 3.1.

• Визначаємо коваріацію:

• Визначаємо коефіцієнт кореляції:

• Визначаємо невідомі коефіцієнти:

• Визначаємо теоретичні значення досліджуваної величини:

b=

• Обчислюємо кореляційне відношення:

• Встановлюємо інтервал довіри:

Y^’=ax+b+S_y

Y^’’=ax+b-S_x

Результати обчислень дозволили отримати наступні дані:

Sx=	13,70609875
Sy=	64,01909437
Кxy=	637,7428571
R=	0,72681222
a=	3,394828897
b=	38,280921
Sy*=	43,97063297

З цього випливає наступна лінійна залежність між кількістю товарів в кошику (X) та часом обслуговування (Y): Y=3,39x+38,28

При цьому:

• a=3,39 - вказує на час (секунди), які затрачуються на сканування штрих-коду одного товару;

• b=38,28 - час, який йде на отримання готівки за покупку чи опрацювання кредитної картки клієнта. Також сюди може входити пакування працівником супермаркету товарів, куплених клієнтом (якщо така послуга передбачається супермаркетом).

З цього випливає, що мінімальний час обслуговування одного клієнта з одним товаром складає y = 3,39*1+38,28 ≈ 42 секунди. Кожен додатковий товар в кошику клієнта додає ще три з половиною секунди.

Очевидно, що отримані дані є усередненими.

Коефіцієнт кореляції, знайдений за умовами задачі, R=0,73 вказує, що існує тісний зв’язок між кількістю товарів в кошику та часом на обслуговування (хоча існують й інші фактори впливу на час обслуговування).

Знайдене кореляційне відношення S_y = 43,97 вказує на яку величину (в секундах) допустимe відхилення часу обслуговування в залежності від кількості товарів в кошику.

Для кращого розуміння результатів задачі нанесемо на графік вхідний масив даних, пряму знайденої лінійної залежності та графіки інтервалів довіри. З цього видно, що існують дві пари значення із вхідного набору значень, які виходять за інтервал довіри - це так звані викиди. Відмітимо, що в реальних аналітичних дослідженнях проводять так звану попередню обробку даних, де дані очищуються від таких викидів (а також, від аномалій, шумів, некоректностей тощо). Такі викиди можуть суттєво впливати на знайдені коефіцієнти a та b.

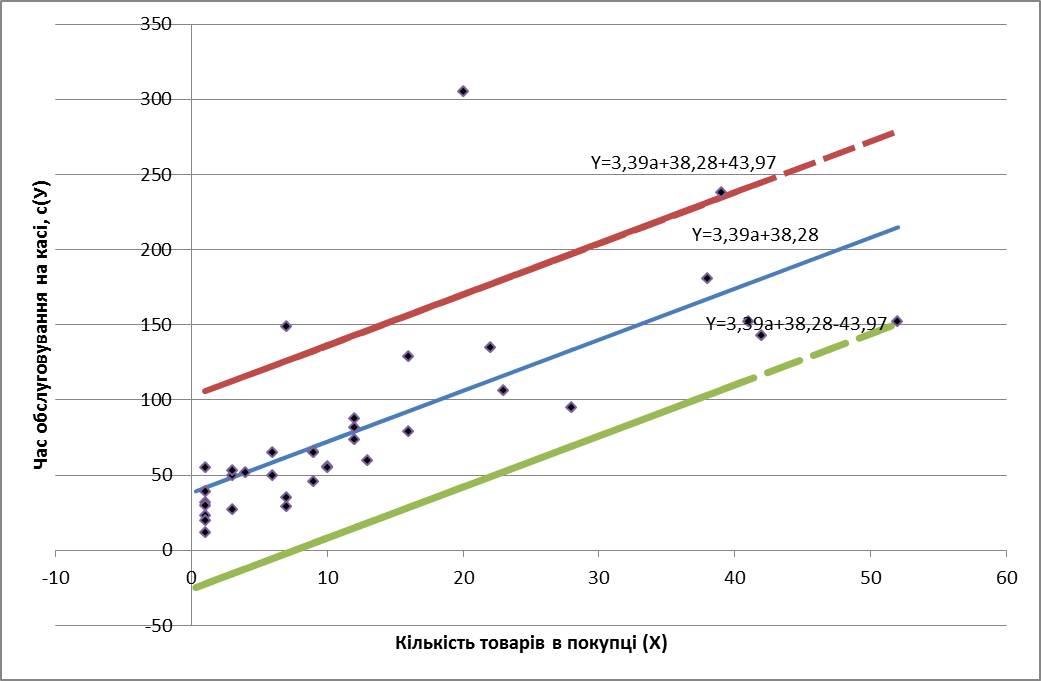
Лінійна залежність: Y=3,39x+38,28

На обслуговування одного товару йде 3,39 секунди.

Час на розрахунок та пакування товарів - 38,28 секунд.

Коефіцієнт кореляції R=0,73 - вказує на існування зв’язку між досліджуваними факторами.

Інтервал довіри: 43,97 секунди.

ІІ. Завдання для самостійної роботи.

(Для визначення числових значень коефіцієнтів використовується: N – Ваш порядковий номер в списку студентів групи, K – остання цифра номеру Вашої групи).

1. Розв’язати задачу 1 згідно свого варіанту

2. Розв’язати задачу 2

Оптові ціни за одну пляшку на марочні вина (у) залежно від року закладки вина (х)

Рік (х)	Ціна (у)
1890	50,00+0,N
1900	35,00+0,N
1920	25,00+0,N
1931	11,98+0,N
1934	15,00+0,N
1935	13,00+0,N
1940	6,98+0,N
1941	10,00+0,N
1944	5,99+0,N
1948	8,98+0,N
1950	6,98+0,N
1952	4,99+0,N
1955	5,98+0,N
1960	4,98+0,N

• Побудувати модель залежності ціни від віку вина;

• Розрахувати коефіцієнти а та b, та інші показники адекватності моделі;

• Побудувати графіки вхідного масиву даних, пряму знайденої лінійної залежності та графіки інтервалів довіри;

• Використовуючи розрахунки, зробити висновки