Контрольні питання.

1. Як записується економетрична модель вибіркової багатофакторної лінійної регресії у матричному вигляді ?

2. Як знаходяться оцінки параметрів багатофакторної лінійної регресії 1 МНК ?

3. Як визначається множинний коефіцієнт кореляції і детермінації, а також їх відмінність від відповідних коефіцієнтів для парної лінійної моделі?

4. За яким критерієм і як здійснюється перевірка загальної статистичної значимості моделі багатофакторної лінійної регресії ?

5. Що таке дисперсійно – коваріаційна матриця оцінок параметрів моделі, її структура, як вона визначається і для чого використовується ?

6. За яким критерієм і як здійснюється перевірка статистичної значимості параметрів моделі багатофакторної лінійної регресії ?

7. Для чого і як будуються інтервали довіри параметрів моделі багатофакторної лінійної регресії ?

8. Для чого і як будуються прогнози для моделі багатофакторної лінійної регресії ?

9. Як оцінити абсолютний граничний вплив кожної пояснюючої змінної багатофакторної лінійної економетричної моделі на залежну змінну ?

10. Як оцінити відносний вплив кожної пояснюючої змінної багатофакторної лінійної економетричної моделі на залежну змінну ?

11. Як оцінити силу впливу кожної пояснюючої змінної багатофакторної лінійної економетричної моделі на залежну змінну ?

12. Чим відрізняються коефіцієнти парної та часткової кореляції?

13. Як визначаються дисперсія залишків, загальна дисперсія і дисперсія регресії? Який між ними зв’язок?

14. Як визначається F-критерій? Для чого він застосовується?

15. Покажіть залежність між F-критерієм і .

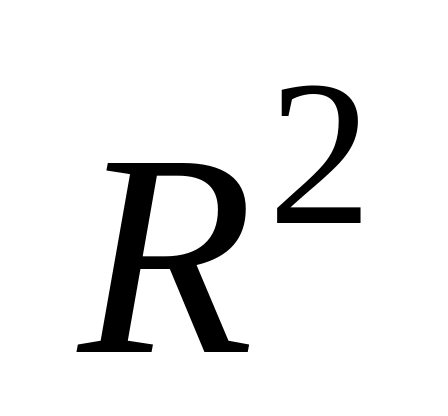16. Як оцінити вірогідність коефіцієнта кореляції?

17. Доведіть, чому для визначення значущості параметрів моделі можна застосувати t-критерій?

18. Як обчислюється t-критерій?

19. Що таке стандартна помилка оцінок параметрів моделі. Наведіть альтернативні формули для її обчислення.

20. Як визначити довірчі інтервали для параметрів моделі?

Лабораторна робота 11-12 Мультиколінеарність. Дослідження наявності мультиколінеарності між змінними за допомогою алгоритму Фаррара-Глобера

Мета: навчитися виявляти мультиколінеарність в моделі за алгоритмом Феррара–Глобера

Теоретичні відомості

При побудові структури регресії, з одного боку, потрібно включити в регресію всі фактори, які мають суттєвий статистичний вплив на показник, а з іншого боку, потрібно, щоб була виконана умова лінійної незалежності між факторами. Якщо існує лінійна залежність хоча б між двома факторами, то говорять, що між цими факторами існує мультиколінеарність.

Для того щоб скористатись МНК для обчислення параметрів регресії необхідно, щоб була відсутня лінійна залежність між факторами, тобто необхідно позбавитися від мультиколінеарності. Існує багато методів дослідження мультиколінеарності. Основна частина цих методів полягає в дослідженні кореляційної матриці. В економетричних задачах для дослідження наявності мультиколінеарності широко застосовується метод Фаррара-Глобера.

Алгоритм Феррара–Глобера:

1. Нормалізувати змінні x_1, x_{2, …,} x_n економетричної моделі:

, де n – кількість вибірки;

– сереньоарифметичне j–ї незалежної змінної.

– дисперсія j–ї незалежної змінної.

Побудуємо матрицю , елементами якої є нормалізовані змінні x_ij^*.

2. Знайти кореляційну матрицю R:

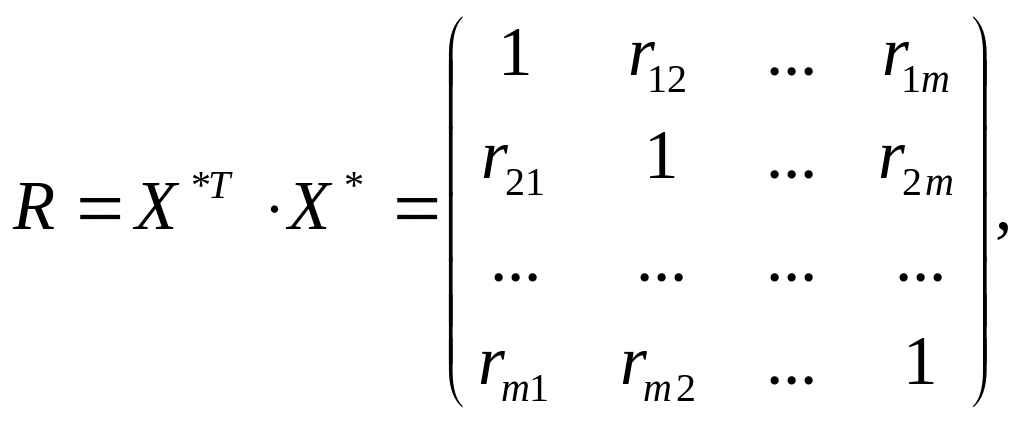
де X^*Т – транспонована Х^*; – парні коефіцієнти кореляції.

Елементи r_ij матриці характеризують щільність зв’язку між змінними і та j.

Якщо на діагоналі матриці R стоять не «1», перетворюємо матрицю наступним чином: на діагоналі записуємо «1», а до інших елементів матриці додаємо різницю між «1» та відповідним діагональним елементом (1– ).

3. Знайти визначник матриці R det R = |R| та розрахункове значення критерію χ²:

.

Порівняємо розрахункове значення з табличним (додаток Г) з ступенями свободи та рівнем значущості q=5%.

Якщо > , то в масиві незалежних змінних має місце загальна мультиколінеарність.

4. Перевірити вибірку на наявність частинної мультиколінеарності за критерієм Фішера. Для цього розрахуємо обернену до R матрицю С:

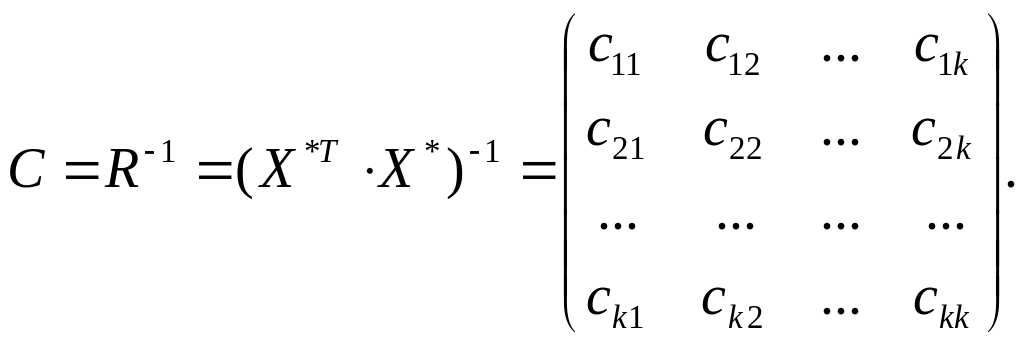
Знайти F–критерій для кожної незалежної змінної за формулою

,

де – діагональні елементи матриці С;

n – кількість спостережень (обсяг вибірки);

m – кількість незалежних змінних.

Розрахункові значення порівнюємо з табличними при (n–m) та (m–1) ступенях свободи та рівні значущості q=5%. Якщо F_р>F_табл., то між незалежними змінними існує мультиколінеарність.

5. Розрахувати коефіцієнти детермінації для кожної незалежної змінної за формулою:

6. Знайти матрицю частинних коефіцієнтів кореляції, які характеризують щільність зв’язків між двома змінними за умови, що всі інші змінні, а саме x_l1, x_{l2, …,} x_lk не впливають на цей зв'язок (існування парної мультиколінеарності):

7. Розрахувати t–критерій для кожної незалежної змінної за формулою

Розрахункові значення порівнюємо з табличним значенням розподілу Стьюдента при (n–m) ступенях свободи та рівнем значущості q=5%. Якщо , то спостерігається мультиколінеарність між двома досліджуваними факторами.