Лабораторна робота 7-8 Побудова двофакторної лінійної моделі ч.1 Дослідження адекватності двофакторної лінійної моделі ч.2

Мета: навчитись будувати двофакторну лінійну модель на прикладі продуктивності праці на підприємстві.

Теоретичні відомості

Всі процеси мають розглядатися у взаємозв'язку. Явище, яке залежить від багатьох факторів, можна описати за допомогою множинної регресії. Найпростішим випадком такої регресії є двофакторна регресія. В моделі двофакторної лінійної регресії досліджується залежність між групою факторів і показником .

Це може бути зміна курсу долара до гривні залежно від часу, зміни доларового курсу гривні, рівня емісії, процентної ставки НБУ та інших факторів. Іншим прикладом може бути зміна рівня злочинності в Україні залежно від зміни факторів: рівня безробіття, заробітної плати, рівня алкоголізму і наркоманії тощо.

В такик моделях спочатку виявляються причинно-наслідкові відношення між показником та факторами. На основі спостережуваних даних дістається регресія. З'ясовується суттєвість впливу визначених факторів на показник. Перевіряється адекватність прийнятої форми залежності спостережуваним даним. Далі робиться аналіз, прогнозування зміни показника та інше.

Для розрахунку параметрів множинної регресії використовують МНК у матричній формі:

, де

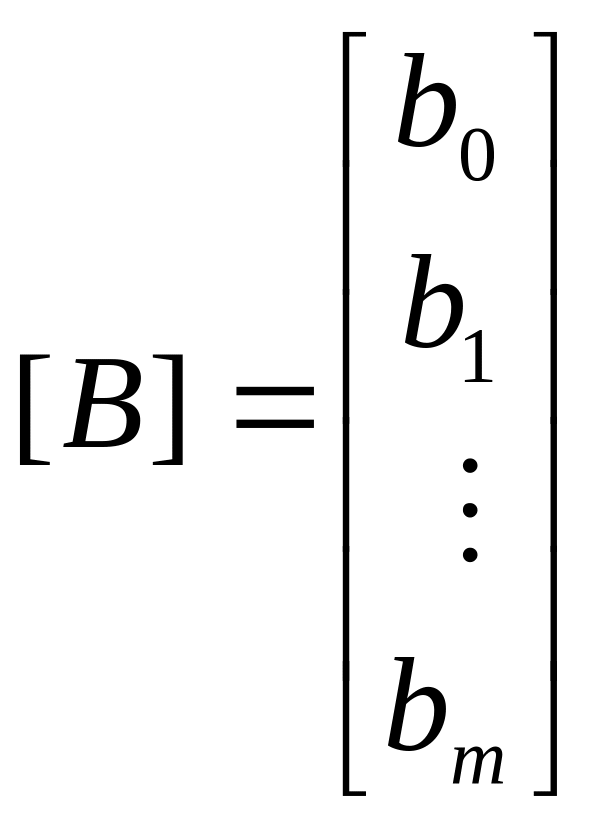– матриця-стовпець оцінок параметрів регресійної моделі;

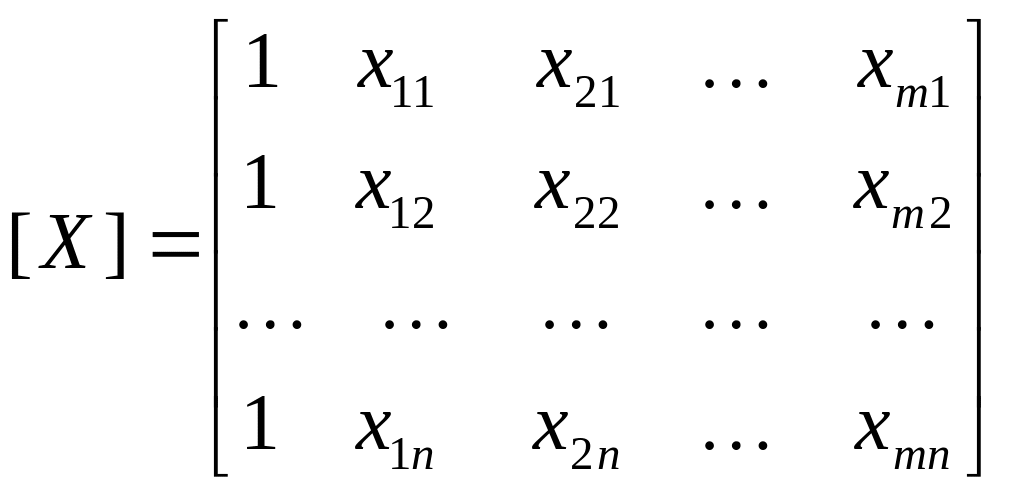– матриця спостережуваних значень факторів, , ; ;

- фіктивний фактор, всі значення якого дорівнюють одиниці;

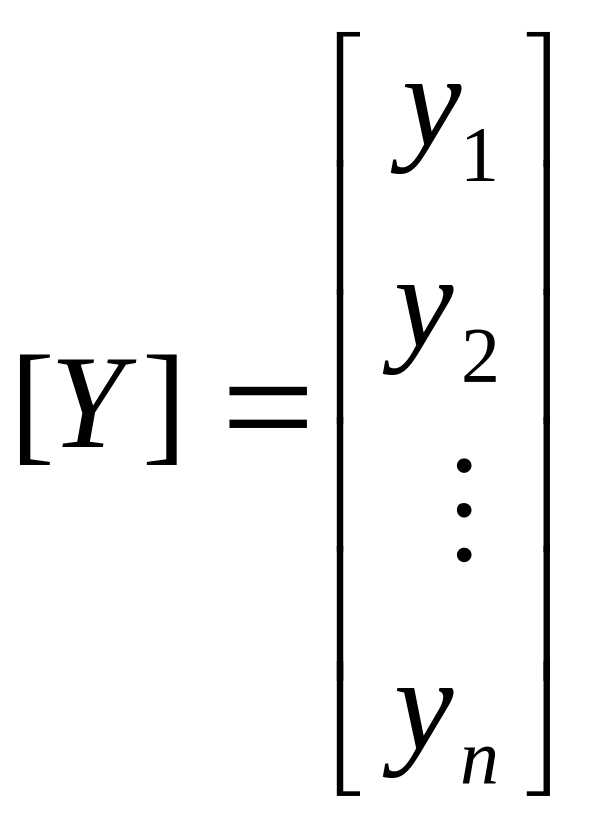– матриця-стовпець спостережуваних значень показника.

Оцінки параметрів регресії можна також знайти, використовуючи вбудовану статистичну функцію LINEST(ЛИНЕЙН).

Порядок знаходження оцінок параметрів регресії з використанням функції LINEST:

1. Відмічаємо блок, де мають знаходитись розрахункові дані: ширина блоку дорівнює числу оцінюваних параметрів, а висота дорівнює п'яти рядкам

2. Відкриваємо функцію LINEST(ЛИНЕЙН)

3. У наступному діалоговому вікні вводимо: в перше поле блок даних показника, у друге поле – блок даних факторів; в третїй рядок вводиться слово ИСТИНА, якщо не дорівнює нулю, і слово ЛОЖЬ, якщо дорівнює нулю; в четвертий рядок вводиться слово ИСТИНА, якщо необхідно знайти не лише параметри лінії регресії, а й додаткову регресійну статистику. Якщо необхідно знайти лише параметри лінії регресії, то вводимо слово ЛОЖЬ

4. Закінчуємо введення формули натисканням комбінації клавіш Ctrl+Shift+Enter.

Таким чином, таблиця розрахункових значень додаткової регресійноі статистики має наступну структуру:

b2	b1	b0
r2	S
Fp	n-m

У першому рядку знаходяться оцінки параметрів множинної лінійної регресії відповідно .

У другому рядку знаходяться середньоквадратичні відхилення оцінок параметрів .

У третьому рядку в першій комірці знаходиться коефіціент детермінації, а в другій комірці – середньоквадратичне відхилення показника.

У четвертому рядку в першій комірці знаходиться розрахункове значення F-статистики, в другій комірці знаходиться (n-k) – число ступенів вільності.

У п'ятому рядку в першій комірці знаходиться сума квадратів відхилень розрахункових значень показника від його середнього значення, в другій комірці – залишкова сума квадратів.