Завдання для самостійної роботи

1. Підберіть два – три висловлювання видатних людей про математику, які Вам найбільше сподобалися.

2. На основі власного досвіду вивчення математики, а також пережитих емоцій при вивченні деяких тем або при вдалому розв’язанні якоїсь математичної задачі, створіть свій вислів про математику (математиків), її призначення, місце в реальному житті тощо.

3. Напишіть коротенького листа тій людині, яка мала найбільший вплив на Ваш вибір майбутньої професії математика.

1.2. Для чого вивчати математику?

Математику вже тому вивчати слід,

що вона розум до ладу приводить.

Михайло Ломоносов

Виступаючи в 1992 році перед учителями, академік В.І. Арнольд¹⁴ так розпочав свою лекцію «Для чого ми вивчаємо математику?»: «У 1267 році на це питання уже відповів англійський філософ Роджер Бекон: «Той, хто не знає математики, не може пізнати жодної іншої науки і навіть не може усвідомити свого невігластва». Власне, на цьому можна було б закінчити лекцію, але люди думають, що, можливо, за сім століть щось змінилося».

То чому ж математиці відводять таку винятково важливу роль в інтелектуальному розвитку особистості? У чому її пізнавальна сила? Як математика впливає на людську культуру взагалі?

Навчальні шкільні програми з математики незмінно визначають метою навчання інтелектуальний розвиток учнів, формування прийомів логічного мислення, просторових уявлень і уяви, пам’яті, уваги, інтуїції, умінь аналізувати, класифікувати, узагальнювати, робити умовиводи за аналогією, отримувати наслідки з даних передумов шляхом несуперечливих міркувань тощо. Тобто саме математиці відведена місія формування інтелектуально розвиненої, творчої особистості. І це не випадково. Саме у процесі занять математикою людина навчається мислити. Тому, що, як зазначає визначний російський математик, академік П. С. Александров¹⁵, «можливо, ніде людське мислення не виступає із такою силою і так яскраво, як у математиці». Це в усі часи визнавали усі великі мислителі. Недаремно Платон при вході у свою Академію, яка мала об’єднати усі форми людської культури і творчості, написав: «Нехай не увійде сюди ніхто, хто не знає геометрії» (у ті часи слово «геометрія» означало математику загалом). Математику він уважав основною сходинкою на шляху до філософського мислення.

Очевидно, за часів Платона не протиставляли «фізиків» (сюди зараховують і математиків) і «ліриків» (тобто гуманітаріїв). На жаль, сьогодні побутує думка про те, що «гуманітарний» склад мислення не сприяє засвоєнню математики і, взагалі, «для чого вивчати математику людині, яка хоче стати філологом (юристом, істориком, психологом, дизайнером, архітектором, менеджером тощо)»? А в гуманітарно орієнтованих людей математика часто викликає неприйняття, а то й відразу. І справа тут не в самій математиці, а в певному стереотипі, сформованому, зокрема, невмілим її вивченням і викладанням. Але про ці проблеми мова піде трохи згодом.

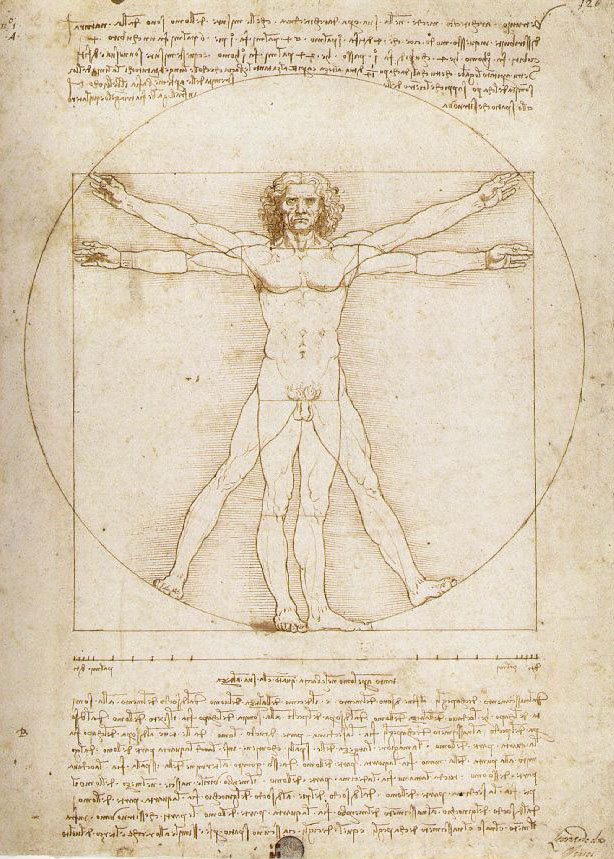
Штучність і невиправданість бар’єру між умовними фізиками і умовними ліриками підтверджується багатьма прикладами. Наведемо лише кілька з них. Уже згадуваний видатний математик Андрій Колмогоров відомим і як авторитетний мовознавець та історик. Яскравим прикладом «універсальної людини» є Леонардо да Вінчі¹⁶, великий художник (живописець, скульптор, архітектор) епохи Відродження, автор знаменитої Джоконди, письменник, який у той же час був талановитим інженером-конструктором, зробив чимало відкриттів у фізиці (оптика, механіка), математиці (геометрія), геології.

Леонардо да Вінчі Автопортрет	Вітрувіанська людина. Рисунок Леонардо да Вінчі. Тепер цей рисунок називають канонічними пропорціями. Вітрувіанська людина – одне із найбільш упізнаваних зображень.

Прояви багатогранності таланту можна знайти й серед сучасних українських науковців. Визнаний фахівець у галузі фізики напівпровідників, доктор фізико-математичних наук Максим Стріха (нар. 24 червня 1961 р.) є автором книги віршів «Сонети та октави» (1991), двох літературознавчих монографій та багатьох статей, сформулював і обґрунтував концепцію націєтворчої функції українського художнього перекладу. В його перекладах виходили українською мовою поетичні й прозові твори Аліг’єрі Данте, Емілі Дікінсон, Роберта Стівенсона, Ред’ярда Кіплінга, Едгара По, Томаса Еліота та інших класиків і сучасних авторів.

Наведені приклади свідчать про те, що «фізик» і «лірик» можуть «жити» в одній особі, що між образним і логічним стилями мислення нема антагонізму. Цілком можливо, що таке поєднання притаманне лише видатним особистостям. Однак, стати професіоналом у будь-якій сфері неможливо без розвиненого мислення. Чому ж заняття математикою якнайкраще сприяють інтелектуальному розвитку? Насамперед тому, що математика, вимагаючи спиратися у своїх умовиводах лише на аксіоми або доведені факти, привчає до строгості мислення, а знайомство із властивостями нескінченних множин розвиває уяву. Хтозна, чи доведеться коли-небудь, скажімо, філологу використовувати у професійній діяльності аксіоматичний метод чи нескінченні множини, однак уміння мислити (а, отже, й грамотно висловлювати думку) і уява йому не завадять.

Наведемо один фрагмент із книги В.А. Успенського¹⁷ «Апологія математики»: «Наприкінці XIX століття в одній із великих аудиторій Московського університету була оголошена лекція на тему «Чи є інтелект у тварин?» Зібралися кілька десятків чи навіть сотень заінтригованих слухачів. Головував заслужений ординарний профессор математики Московського університету Микола Васильович Бугаєв, президент Московського математичного товариства і батько Андрія Бєлого. Перед початком лекції він звернувся до аудиторії із запитанням, чи знає хто-небудь, що таке інтелект. Відповідь виявилася негативною. Тоді Бугаєв оголосив, що, оскільки ніхто з присутніх не знає, що таке інтелект, лекція про те, чи є він у тварин, відбутися не може». Це типовий приклад непрямого впливу «математичного» мислення на мислення «гуманітарне». Він також підкреслює, що роль математичної освіти не в тому, щоб розв’язати проблеми, які виникають у різних галузях науки чи практичної діяльності, зокрема, й гуманітарних, а в тому, щоб допомогти фахівцям цих галузей краще усвідомити суть цих проблем і критично поставитися до спроб їх розв’язання.

У цьому сенсі заняття математикою можна порівняти зі стройовою підготовкою в армії. Навряд чи в умовах реального бою солдат ходитиме стройовим кроком, але в усіх арміях світу стройова підготовка – неодмінна складова військового навчання, оскільки дисциплінує дії і тренує уміння виконувати команди. Заняття ж математикою тренують дисципліну мислення, найважливішими ознаками якого є чітке усвідомлення різниці між істинним і хибним, доведеним і гіпотетичним, зрозумілим і незрозумілим, змістовним і беззмістовним.

Зазначимо, що для того, аби кваліфікувати висловлення як хибне, беззмістовне чи незрозуміле, часто потрібні неабиякі вольові зусилля, зокрема, коли щось стверджує «визнаний авторитет». Здатність робити такі зусилля, піддавати сумніву і критичному аналізу, незважаючи на авторитети, також виховує математика, яка за своєю природою є наукою демократичною. На відміну від гуманітарних наук, де переконливість того чи іншого твердження часто залежить від наукового авторитету автора, математична істина не залежить від того, хто її встановив, академік чи школяр або студент. Приступаючи до розв’язання математичної задачі, всі перебувають в однакових стартових умовах і переможе не той, у кого більше титулів, а той, хто краще володіє методами розв’язування задач, інтуїцією і виявиться винахідливішим.

Немає в математиці й «царського шляху». Підтверджує це енциклопедична історія, справжня чи вигадана, про великого математика Евкліда і єгипетського царя Птоломея (інший варіант – Архімеда і сиракузького царя Гієрона). Цар виявив бажання вивчити геометрію і звернувся до математика. Математик почав його навчати, але невдовзі цар обурився, що його навчають точно так, як і всіх інших, не враховуючи його царського статусу, який, на думку царя, передбачав особливий спосіб навчання. На що математик відповів: «Немає царського шляху в геометрії».

Отже, як це не парадоксально, але саме математика, а не політологія, психологія чи ще якась інша гуманітарна наука, якнайкраще виховує таку важливу якість людини, як демократизм.

А може й справді достатньо «призначити» у математиці окремі факти, теореми, задачі на роль «тренажерів мислення», «засобів для гартування волі», і не навантажувати усіх (особливо тих, хто не пов’язує свою професійну діяльність з математикою) великою кількістю понять, фактів, які пропонують шкільні й університетські програми з математики? На жаль, подібні запитання іноді задають і студенти-математики педагогічних спеціальностей, мовляв, для чого нам вища математика, коли у школі викладають лише елементарну?

Спробуємо спростувати таку точку зору.

Почнемо з того, що ніхто від народження не знає, ким стане у майбутньому, із якою сферою діяльності пов’яже своє життя. То чи розумно наперед обмежувати можливості дитини самостійно обирати життєву дорогу? Наведемо, однак, й переконливіші аргументи.

Сьогоднішній світ змінюється шаленими темпами. Не встигла з’явитися нова модель комп’ютера (мобільного телефону, планшета тощо), як вона уже застаріла. А математика – одна із найдавніших наук. І уявіть собі, що безліч фактів, встановлених тисячі років тому назад, використовуються й сьогодні.

Давні єгиптяни навічно увійшли в історію завдяки своїм пірамідам, яких не збудували б, не знаючи простих законів математики. При будівництві пірамід і храмів, щоб отримати прямий кут, мотузку ділили на 12 рівних частин, точки поділу помічали, а кінці мотузки зв’язували. Далі троє людей бралися за мотузку в трьох точках, віддалених одна від одної на 3, 4 та 5 частин і максимально розтягували її, щоб утворився трикутник. Людина, що стояла між ділянками мотузки довжинами 3 і 4 частини, виявлялася у вершині прямого кута. Це свідчить, що єгиптянам була відома теорема Піфагора, і якою успішно користуються й дотепер.

З часом сфера застосування математики поступово розширювалася. Математика проникала у землемірство, будівництво, гідротехніку, мореплавство, торгівлю, геодезію, картографію, небесну механіку, військову справу.

У сучасному світі математика – це мова й інструмент будь-якої, без перебільшення, галузі науки і практичної діяльності людини. Сьогодні без математики важко уявити собі розвиток не лише природничих наук (фізики, астрономії, хімії, біології), інженерної справи, економіки, а й традиційно гуманітарних (соціології, лінгвістики, психології, історії, медицини) і сфера проникнення математики постійно розширюється. Математика стає універсальним ключем до всіх наук. Саме тому навчання математики в школі, як зазначено у навчальних програмах, спрямоване також на формування в учнів математичних знань – невід’ємної складової загальної культури людини, необхідної умови її повноцінного життя в сучасному суспільстві на основі ознайомлення школярів з ідеями і методами математики як універсальної мови науки і техніки, ефективного засобу моделювання і дослідження процесів і явищ навколишньої дійсності.

Характерною рисою математичних моделей є їх універсальність і прикладна ефективність. Неможливо і нерозумно вивчати в математиці лише те, що потрібно на практиці в конкретному часі і в конкретних обставинах. Не менш шкідливо відмовлятися від її вивчення через оманливу «непотрібність». Крен політики останніх десятиліть у галузі математичної освіти в бік практичного прагматизму уже призвів до негативних наслідків математичної підготовки школярів і виховання фахівців для народного господарства. Щоб використати унікальні можливості математики в різних прикладних застосуваннях, потрібна серйозна теоретична математична підготовка й уміння думати, а не натискувати кнопки. Саме ця якість математичної освіти останнім часом погіршилася.

Це правда, що математична модель не завжди дає миттєвий результат і не завжди одразу помітно, де можна її застосувати. Ми уже наводили приклад з комплексними числами, які знайшли своє практичне застосування через чотири століття після їх винайдення. А ось ще одна повчальна історія. Конічні перерізи¹⁸ були відкриті в Давній Греції в ІІІ – ІІ ст. до н.е. А знадобилася ця теорія Йоганнесу Кеплеру¹⁹ у XVI ст., коли він з’ясовував закони руху планет. Його учитель Тіхо Браге протягом двадцяти років вимірював і фіксував положення планет Сонячної системи (спостереження велися неозброєним оком, телескопам у той час астрономи не довіряли). Після смерті учителя Кеплер узявся за математичну обробку результатів спостережень і виявив, що траєкторіями руху планет є еліпси²⁰. Однак цей результат він міг би не отримати, якби не був знайомий із теорією конічних перерізів. Справа в тому, що еліпс мало відрізняється від кола, якщо кут нахилу площини перерізу конуса до його осі мало відрізняється від прямого. Це рівнозначно тому, що ексцентриситет²¹ еліпса малий. Спочатку Кеплер схильний був думати, що орбіта Марса – коло, але, помітивши незначне відхилення положення Сонця від центра і знаючи, що еліпс із малим ексцентриситетом дуже схожий на коло, провів наближені обчислення з більшою точністю і встановив, що орбіта Марса на 0,5% сплюснута в напрямі, перпендикулярному до діаметра, на якому знаходиться Сонце. Так він дійшов висновку, що планети рухаються еліптичними орбітами. (Аналітичне доведення того факту, що орбіти планет мають форму еліпсів (1687 р.), належить Ісааку Ньютону²².)

Таким чином, ніколи не можна із абсолютною впевненістю стверджувати, що якась абстрактна математична теорія (модель) не потрібна, бо не має свого прикладного застосування, оскільки, можливо, саме вона, за прикладом еліпса, колись, хай навіть через тисячоліття, знайде таки свого Кеплера.

Наведемо ще один приклад, який пояснює деякі парадоксальні, на перший погляд, суспільно-економічні процеси. Розпад могутнього Радянського Союзу, зокрема, крах його економіки, здавалися неможливими, оскільки економіка і добробут зростали. Світова економічна криза, яку ми нещодавно переживали, також для більшості була громом серед ясного неба, адже економіка розвинених країн мала позитивну динаміку. Спробуємо математично пояснити причини і механізм будь-якої економічної кризи. Кожен, хто знайомий із поняттям похідної, а вона вивчається сьогодні в школі, знає, що похідна характеризує швидкість зміни функції, а похідна другого порядку – швидкість зміни швидкості, тобто прискорення. І, що постійно від’ємна похідна другого (і, навіть вищого) порядку призведе, врешті решт, до того, що від’ємною стане перша похідна.

Що ж таке економічна криза? Це явище, яке не наступає раптово, одномоментно. Передвісником економічної кризи є спад темпів економічного зростання (друга похідна від’ємна). І якщо навіть економіка зростає (перша похідна додатна), але почався тривалий спад темпів її зростання, то це уже тривожний сигнал. Бо такий стан речей неодмінно призведе в перспективі й до падіння виробництва та добробуту (перша похідна змінить знак з плюса на мінус), причому темпи погіршення ситуації будуть тільки прискорюватися. Унаслідок інерційності системи ніякими, навіть дуже розумними й правильними заходами швидко поліпшити ситуацію не вдається, бо будь-які зміни призводять до зміни знака лише старшої похідної, а перша похідна залишається від’ємною. Тому будь-яка економічна деградація викликана не стільки сьогоднішніми рішеннями, як учорашніми й позавчорашніми, коли виробництво зростало і ситуація здавалася цілком благополучною. Якби ж то ми, а особливо ті, від кого залежить планування економіки, управління соціально-економічними процесами, кажучи словами Тараса Шевченка, «вчились так, як треба».

І ще один красномовний аргумент на користь математичної освіти. Як відомо, Нобелівську премію не присуджують за відкриття в галузі математики. Але майже усі відкриття, удостоєні цієї найпрестижнішої премії в галузях фізики та економіки, позначені печаттю Математики, бо використовують математичні методи дослідження, різноманітні математичні моделі. Зокрема, серед 69 (на сьогоднішній день) лауреатів Нобелівської премії у галузі економіки, понад п’ятдесят є або вченими-математиками, або мають базову математичну освіту, або ж, назвемо їх «математиками-любителями», активно використовують математику у своїх економічних дослідженнях, працюють на стику математики й економіки.

Наприклад, Нобелівський лауреат 1975 р. «за внесок в теорію оптимального розподілу ресурсів» радянський математик Леонід Канторович – доктор фізико-математичних наук, чиї наукові результати збагатили теорію функцій, функціональний аналіз, теорію множин; він один із творців лінійного програмування, яке успішно застосовував в економічній теорії.

Англійський економіст, лауреат Нобелівської премії в галузі економіки (1984 р.) Річард Стоун – доктор фізико-математичних наук, зробив великий внесок в математичне моделювання економічних процесів.

Американський економіст, Нобелівський лауреат (1994 р.) Джон Форбс – учений-математик, математичний геній якого найбільше виявив себе в теорії ігор і диференціальній геометрії. Дисертацію з теорії ігор написав у віці 21 рік, за неї ж через 45 років отримав Нобелівську премію в галузі економіки. Широкому загалу Джон Форбс відомий за драматичним біографічним фільмом Рона Говарда «Ігри розуму», що отримав премію «Оскар» у чотирьох номінаціях.

Ізраїльському вченому-математику Роберту Ауману Нобелівську премію з економіки присудили в 2005 році за розширення розуміння і аналіз проблем конфліктів і співпраці на основі теорії ігор. На думку професора Аумана будь-які конфлікти описуються певними математичними моделями, які піддаються математичному аналізу; ігнорування цих моделей неодмінно веде до фіаско. А економіка, вважає він, це чиста математика і логіка.

І нарешті кілька слів про історію фрази, винесеної в епіграф цього параграфа. Кажуть, що у 1752 році Михайлові Ломоносову доручили проаналізувати викладання фізики, хімії та математики в Кадетському корпусі (з цього елітного закладу у ХVІІІ ст. вийшли майже всі відомі російські діячі – письменники, вчені, військові, адміністратори). Докладно обґрунтувавши необхідність вивчення хімії та фізики, з приводу математики Ломоносов пише лише одну фразу: «А математику вже тому вивчати слід, що вона розум до ладу приводить».