М

Микола Вікторович Працьовитий

(нар. 1959)

икола Вікторович навчався в аспірантурі Інституту математики АН УРСР з 1983 року по 1986 рік за спеціальністю теорія ймовірностей і математична статистика. У 1987 році успішно захистив кандидатську, а в 1998 році – докторську дисертації. Один із перших, разом зі своїм учителем Анатолієм Федоровичем Турбіним, започаткував в Україні дослідження фракталів та розробку фрактальних методів. Наукові інтереси М.В.Працьовитого лежать в області фрактального аналізу та фрактальної геометрії, метричної та ймовірнісної теорії чисел, тощо. Вагомі наукові результати дослідження тополого-метричних і фрактальних властивостей математичних об’єктів започаткували новий напрям у теорії ймовірностей – фрактальний. Сьогодні М.В. Працьовитий очолює в Інституті математики НАНУ відділ фрактального аналізу.

М.В. Працьовитий опублікував 4 монографії та понад 300 наукових і науково-методичних статей. Його роботи добре відомі як в Україні, так і за її межами. Під його керівництвом уже підготовлено і захищено 15 кандидатських і одну докторську дисертації. Проводить велику роботу по розвитку міжнародних наукових зв’язків.

Що таке фрактал?

Фрактал – це нескінченно самоподібна геометрична фігура, кожний фрагмент якої повторюється при зменшенні масштабу. Масштабна інваріантність, що спостерігається у фракталах, може бути або точною, або наближеною.

Фрактальні властивості мають такі природні об’єкти, як сніжинка, якщо її нескінченно «добудовувати»; за фрактальними алгоритмами ростуть кристали, дерева.

Прикладом найпростішого фрактала є «сніжинка Коха» (Рис. 8). Її побудова починається із правильного трикутника, довжина сторони якого дорівнює 1. Сторона трикутника вважається базовою ланкою. Далі, на будь-якому кроці ітерації кожна ланка заміняється на утворюючий елемент – ламану, що складається по краях з відрізків довжиною 1/3 від довжини ланки, між якими розміщаються дві сторони правильного трикутника зі стороною в 1/3 довжини ланки. Усі відрізки – сторони отриманої кривої вважаються базовими ланками для наступної ітерації. Крива, що одержується в результаті n-ї ітерації, при будь-якому n, називається передфракталом, і лише при 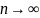крива Коха стає фракталом. Отримана в результаті ітераційного процесу фрактальна множина є лінією нескінченної довжини, що обмежує скінченну площу. Справді, на кожному кроці число сторін результуючого багатокутника збільшується в 4 рази, а довжина кожної сторони зменшується тільки в 3 рази, тобто довжина багатокутника на n-ій ітерації дорівнює і прямує до нескінченності при необмеженому збільшенні n. А площа фігури, обмеженої фракталом дорівнює .

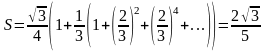Фракталом є також так звана Канторова множина – точкова множина числової прямої, із якою ви зустрінетеся на старших курсах при вивченні теорії функцій дійсної змінної та функціонального аналізу.

Приклади фракталів зображені на рис. 9 Слід сказати, що, завдяки своїй самоподібності, фрактали – дуже красиві геометричні об’єкти, варті, щоб ними захоплюватися і милуватися як справжніми художніми витворами (див. напр. https://www.google.com.ua/search?q=%D1%84%D1%80%D0%B0%D0%BA%D1%82%D0%B0%D0%BB%D0%B8&hl=ru&client=firefox&hs=7u9&tbo=u&rls=org.mozilla:ru:official&tbm=isch&source=univ&sa=X&ei=0H68UM_5LNHotQb6m4DgCQ&ved=0CE8QsAQ&biw=1600&bih=717).

Щоб знайти інші сторінки сайту, на яких зображено фрактали, достатньо у будь-якій пошуковій системі Інтернету задати ключове слово «фрактал» та запустити пошук.

У наш час фрактали застосовують при аналізі структур ландшафтів, отриманих аерокосмічною зйомкою, для вивчення поверхонь пористих середовищ, вони виявилися ефективними при розпізнаванні образів на радіолокаційних зображеннях, стисненні інформації та ін. Однак, щоб зрозуміти природу фракталів, спосіб їх побудови, суть фрактальних методів потрібні глибокі знання багатьох математичних дисциплін, зокрема, теорії ймовірностей, функціонального аналізу, топології та ін.

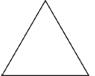
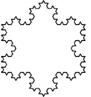
Рис. 8. Перші 5 ітерацій сніжинки Коха

Рис. 9. Приклади фракталів

Математичні школи в Інституті математики НАН України⁷⁵

Рисунок наукового дерева в окремому файлі