2. Приклади характерних задач з розв’язанням

Задача 1. Написати розподіл Максвелла в декартових, циліндричних і сферичних координатах простору швидкостей. Одержати розподіл Максвелла за абсолютною величиною швидкості.

Розв’язання. Розподіл Максвелла за компонентами швидкості деякої частинки випливає з канонічного розподілу Гіббса і має вигляд

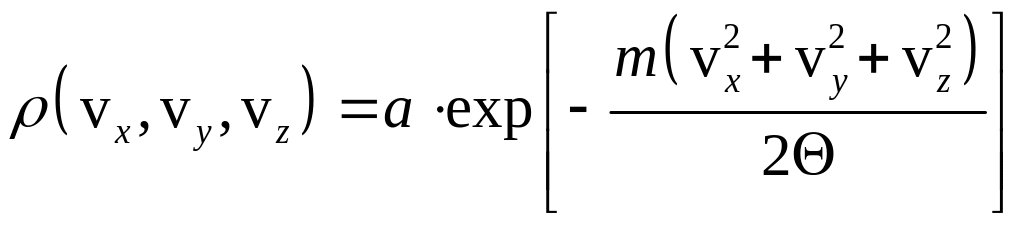. (1)

Константу а знаходимо з умови нормування

,

.

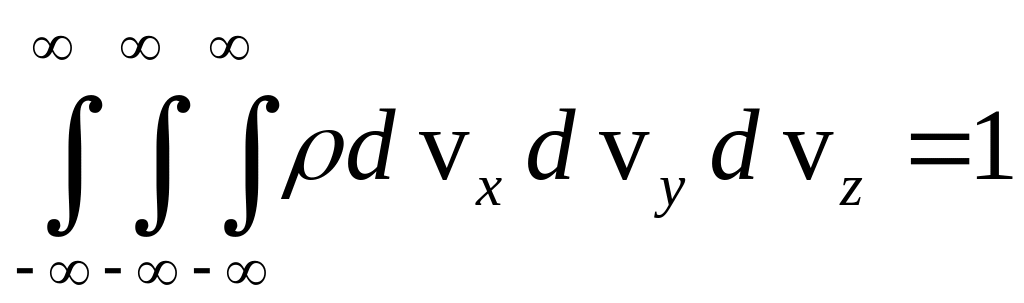У довільних координатах , , розподіл Максвелла матиме вигляд

,

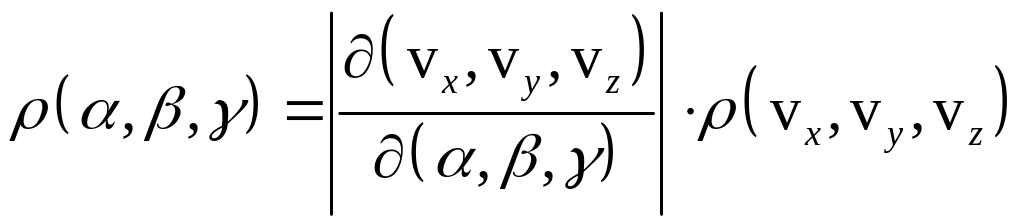де  якобіан перетворення .

У випадку циліндричних координат маємо 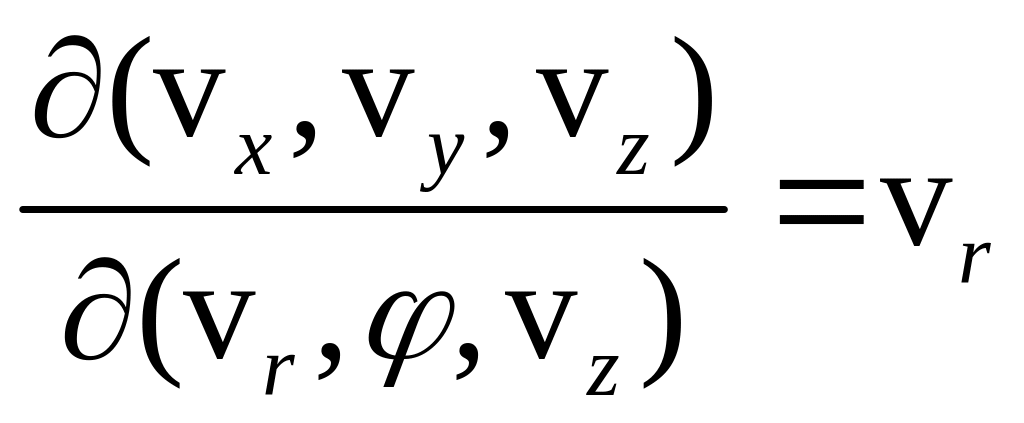, тому

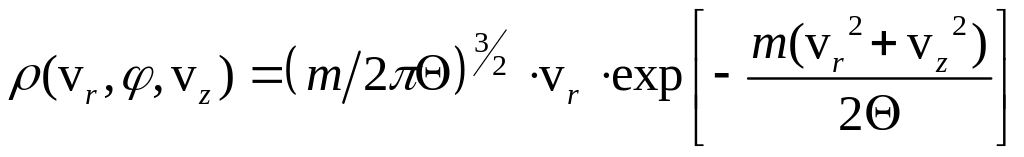. (2)

У випадку сферичних координат відповідний якобіан дорівнює

,

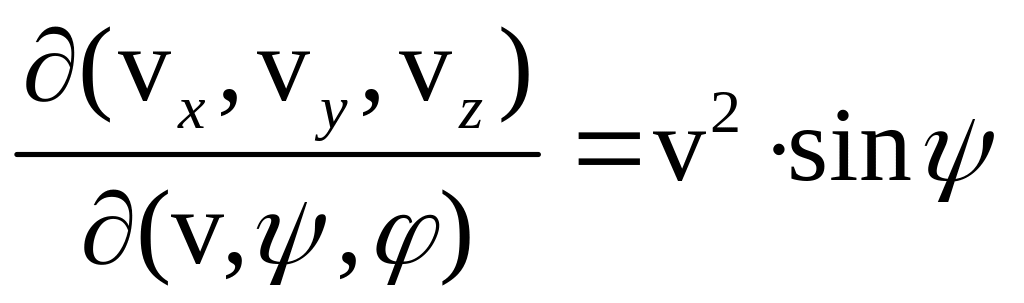тому

.

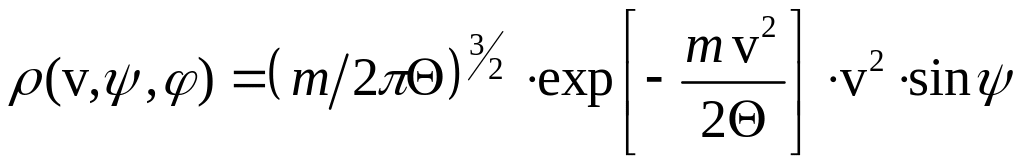Інтегруючи за кутами , , одержуємо класичний розподіл Максвелла за абсолютною величиною швидкості:

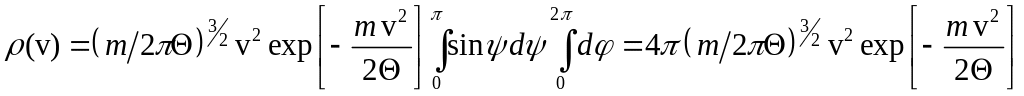. (3)

Задача 2. Використовуючи розподіл Максвелла за абсолютною величиною швидкості молекули газу, знайти розподіл за її кінетичною енергією.

Розв’язання. Розподіл Максвелла за кінетичною енергією одержимо з рівності (інваріантність імовірності)

.

Отже, з урахуванням, що , остаточно маємо:

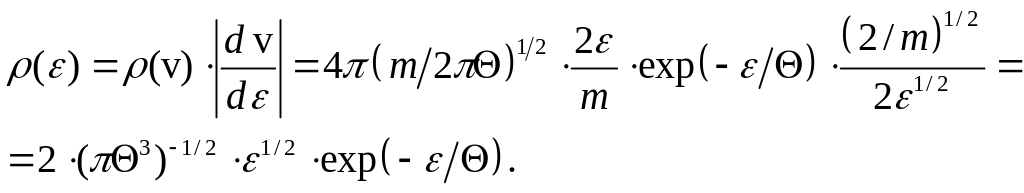(1)

Задача 3. Визначити відношення чисел частинок, які мають енергію менше і більше заданого значення .

Розв’язання. Шукане відношення можна записати через відношення відповідних ймовірностей:

.

Використовуючи розподіл за кінетичною енергією, (формула (1) попередньої задачі), одержимо:

.

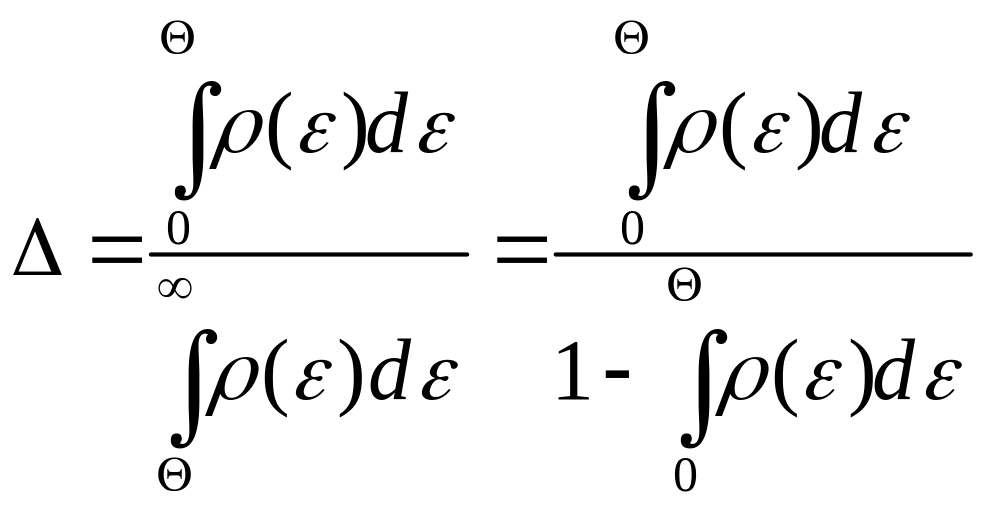Отже,

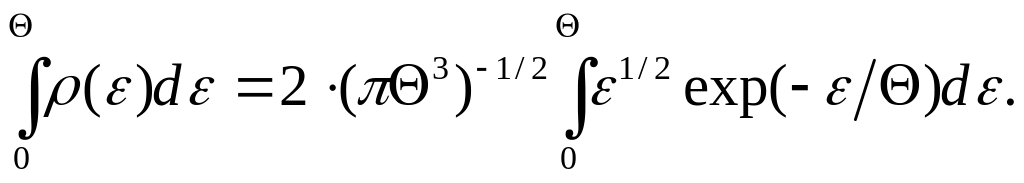
Інтегруючи частинами, матимемо

.

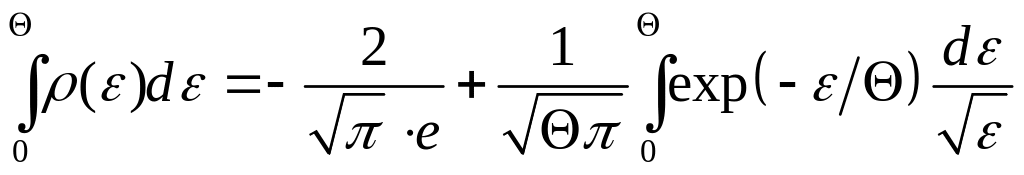Заміна зводить останній інтеграл до спеціальної функції :

.

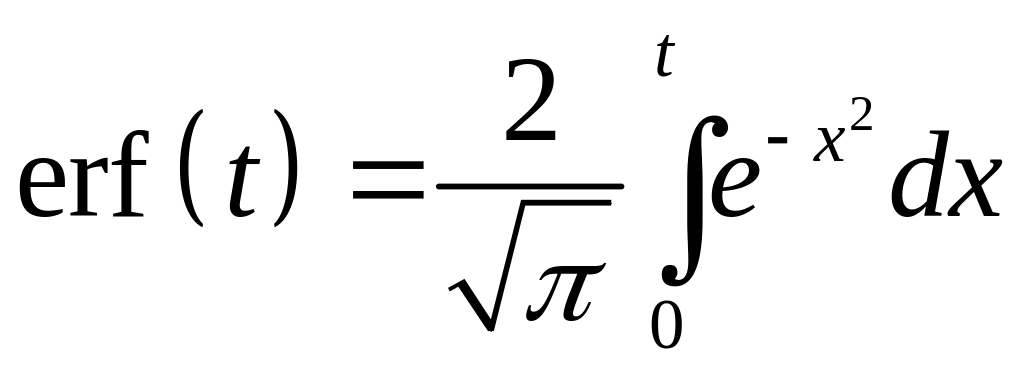Таким чином,

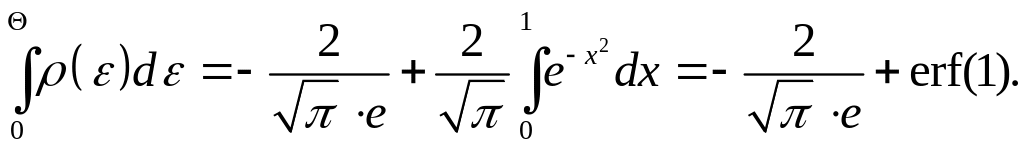
З таблиць знаходимо . Остаточно

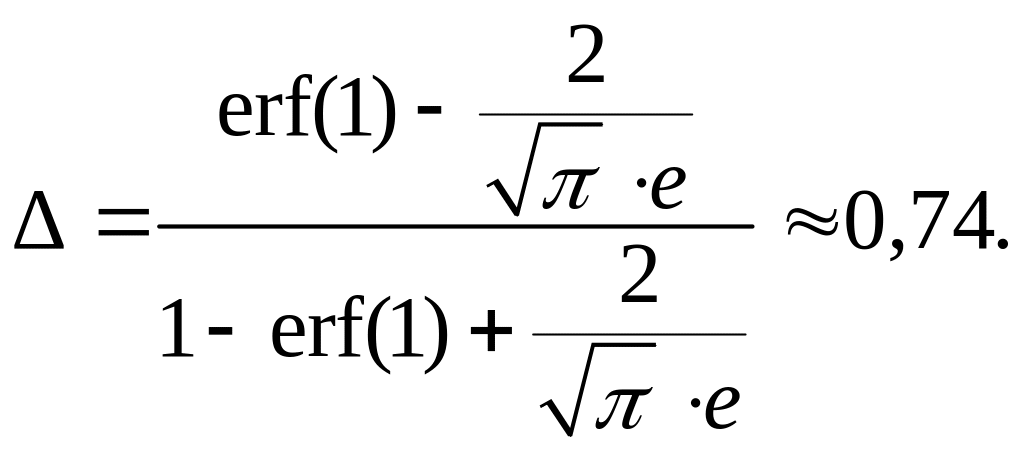
Задача 4. Обчислити тиск газу на стінку посудини, якщо концентрація частинок газу дорівнює , а температура . Визначити повне число частинок, що падають за 1 с на 1 см² стінки.

Розв’язання. Обчислимо тиск ідеального газу , користуючись ізотропією теплового руху молекул. Для цього розглянемо частинок, які незалежно одна від одної рухаються у сфері радіуса R із швидкостями , розподіленими за Максвеллом. Нехай деяка частинка має швидкість . Як і всі частинки, вона рухається в площині великого кола сфери і незалежно від кута зіткнення з нею віддає сфері однаковий імпульс за одиницю часу. Для спрощення обчислень приймемо, що частинка рухається у сфері вздовж її діаметра. Тоді за час вона віддаватиме сфері імпульс , тобто створюватиме тиск

,

де т  маса частинки, – площа сфери.

N частинок, таким чином, створюватимуть тиск

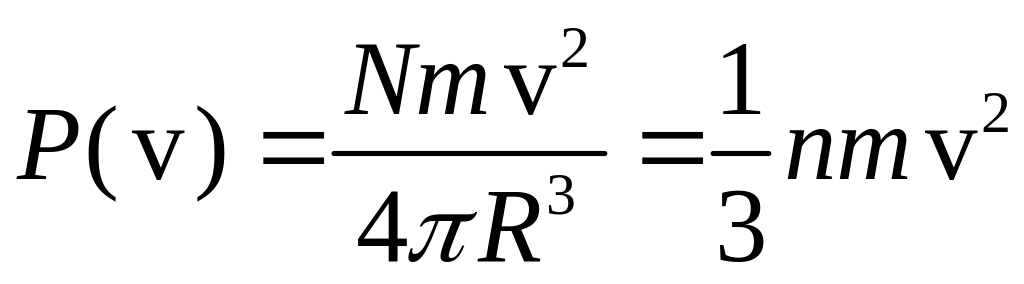, (1)

де 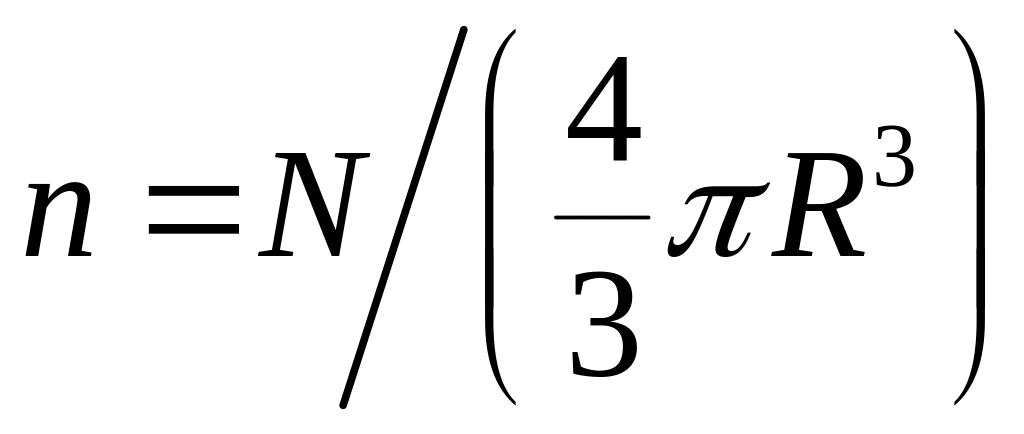– густина частинок.

Остаточний результат знайдемо як середнє значення величини з (1) за розподілом Максвелла (формула (1) першої задачі):

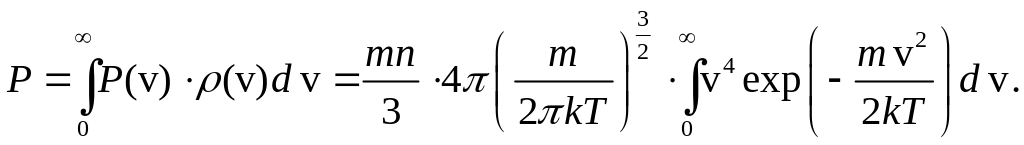
Оскільки 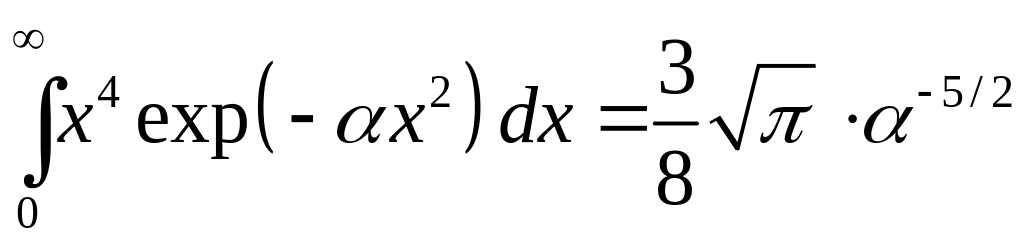(див. формули (7) задачі 1 з розділу 11), матимемо: , що є термічним рівнянням стану ідеального газу.

Визначимо тепер кількість молекул, що стикаються з 1 см² площі стінок за 1 с (густина потоку). Виберемо вісь ОХ перпендикулярно стінці з площею S. Тоді частинки з компонентою швидкості долітатимуть до неї за час , де –- відстань до стінки вздовж вісі ОХ. Кількість таких частинок становитиме . Густину потоку знайдемо як

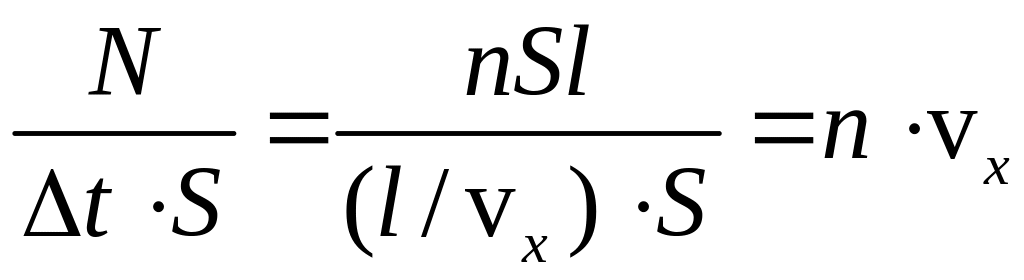(2)

Узявши середнє від за розподілом Максвелла (формула (1) першої задачі) (враховуємо, що ), остаточно знайдемо густину потоку :

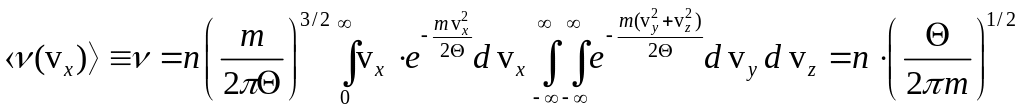. (3)

Задача 5. Ідеальний газ з частинок перебуває в однорідному полі тяжіння при температурі в нескінченному циліндрі перетином на поверхні Землі. Визначити розподіл тиску газу по висоті, координату центра мас газу і середню потенціальну енергію молекул.

Розв’язання. Нехай вісь ОХ має напрямок вертикально вверх від поверхні Землі. Тоді за розподілом Больцмана для концентрації частинок на висоті х можна записати:

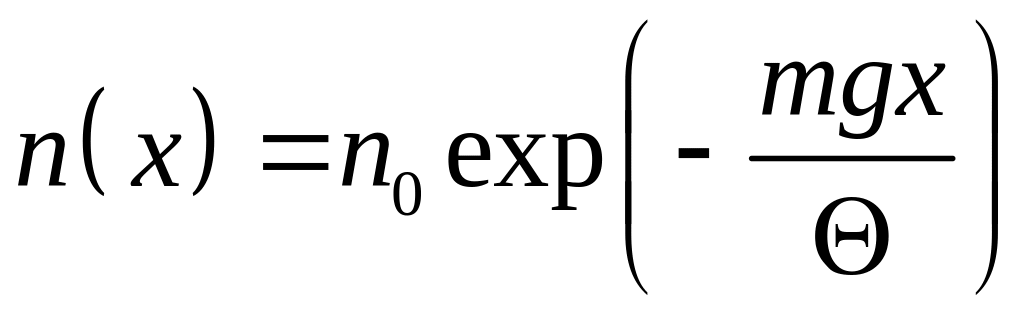, (1)

де – концентрація біля поверхні Землі (коли ). Оскільки

,

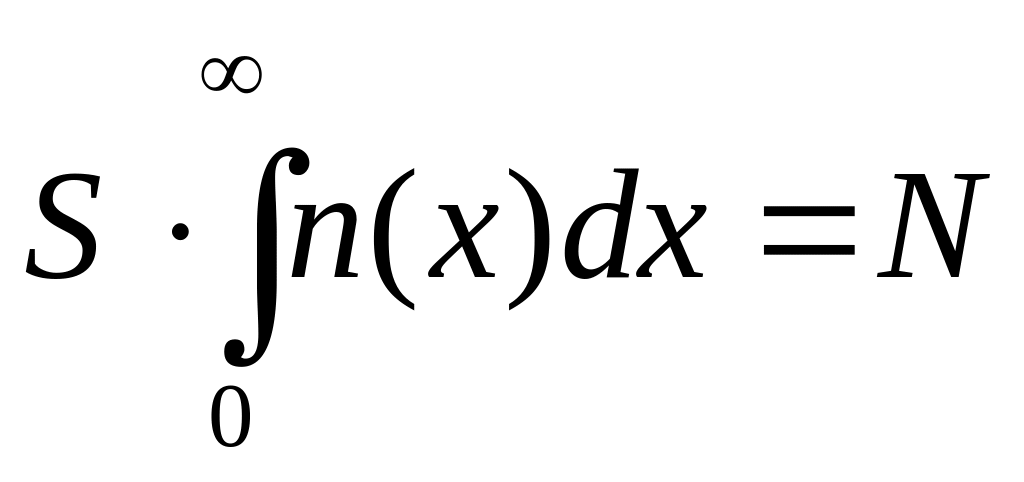маємо

.

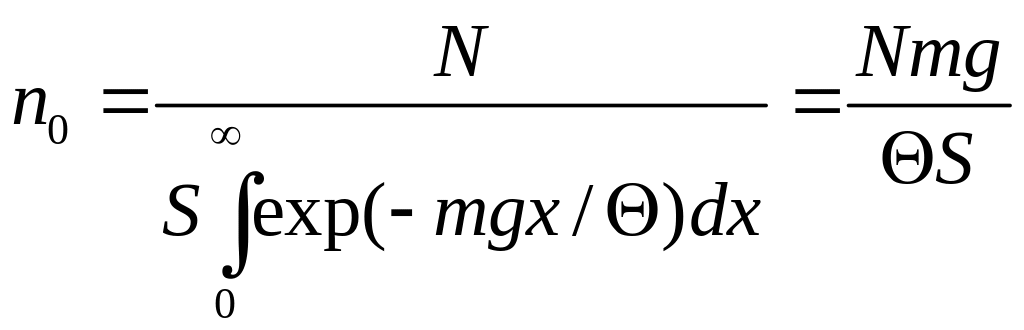Тиск Р ідеального газу дорівнює , а на висоті х:

.

Координату центра мас х_с циліндра, що розглядається, знайдемо за формулою

.

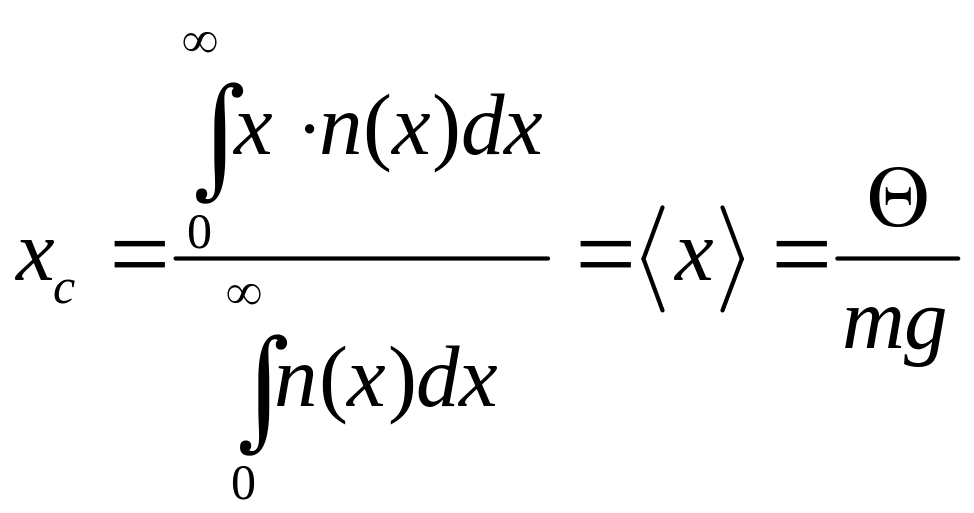Тоді середня потенціальна енергія становитиме

.

Задача 6. Показати, що земна атмосфера не може перебувати в статистичній рівновазі і безупинно розсіюється в простір.

Розв’язання. Густина ідеального газу в потенціальному полі визначається розподілом Больцмана:

,

де  густина газу у тих точках, де .

Гравітаційне поле Землі визначається законом тяжіння Ньютона, де потенціальна енергія u прямує до нуля на нескінченності. Це призводить до того, що густина у скільки завгодно далеких точках повинна бути скінченною величиною згідно з розподілом Больцмана. Але ж для скінченного числа N частинок це неможливо. Тобто в гравітаційному полі Землі атмосфера не може перебувати в рівновазі і повинна безперервно розсіюватися в простір. Формально ця ситуація відповідає тому, що статистичний інтеграл для газу в такому гравітаційному полі розбігається.

Задача 7. Визначити розподіл чисельної густини ідеального газу з частинок у центрифузі радіуса і довжини , що обертається з кутовою швидкістю . Температура газу . Обчислити середню потенціальну енергію молекул газу.

Розв’язання. У системі координат, що зв’язана з центрифугою, діятиме відцентрова сила . Потенціальна енергія молекули в полі цієї сили становитиме

,

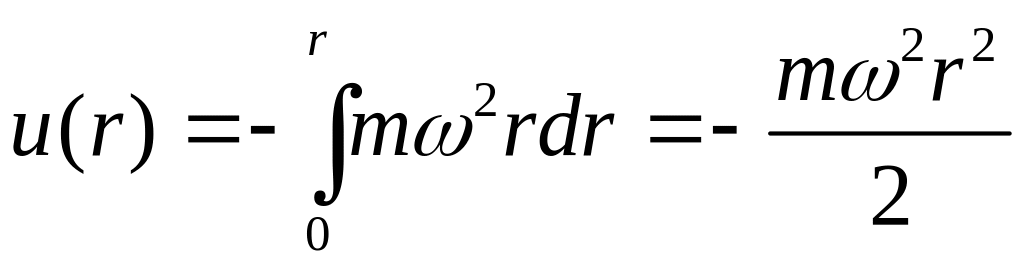де відстань r відраховується від осі обертання. Тому густину газу згідно з розподілом Больцмана можна записати у вигляді

(1)

Сталу А знаходимо з умови нормування

,

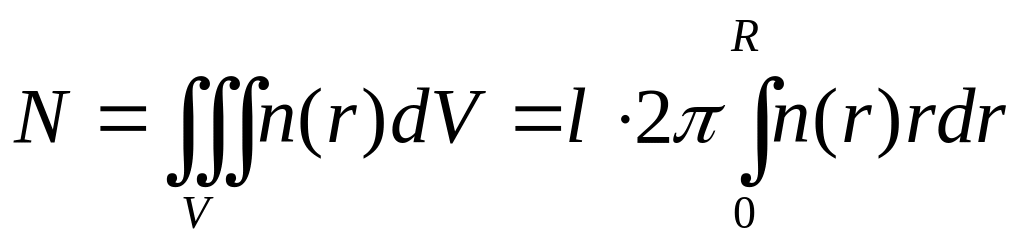звідки

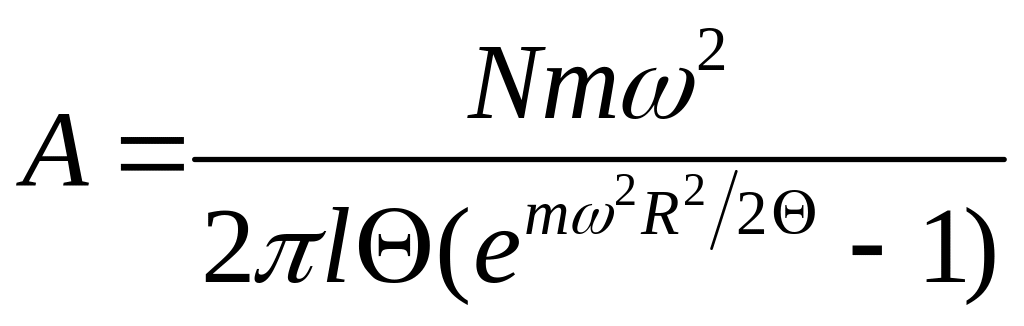. (2)

Середня потенціальна енергія молекул газу, яка припадає на одну молекулу дорівнюватиме

,

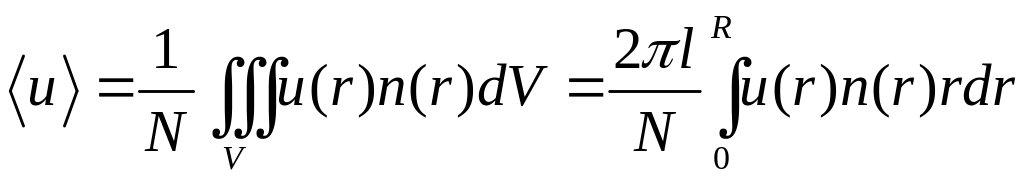що з урахуванням (1) та (2) остаточно дає

.

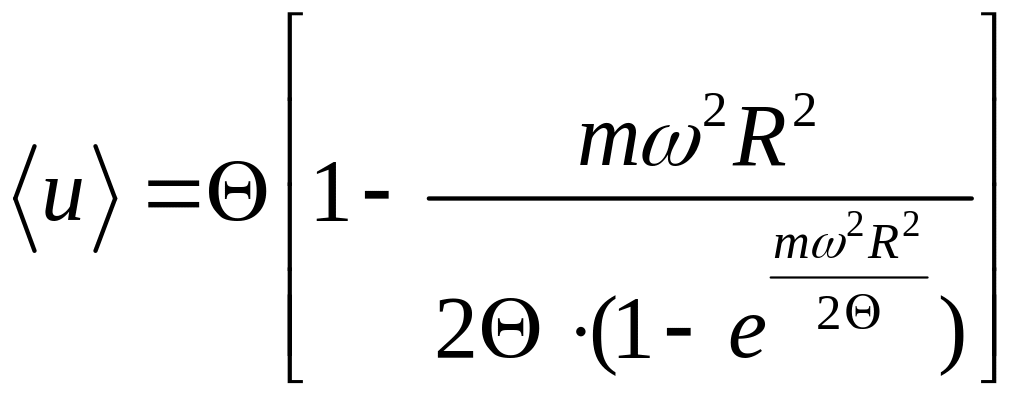Задача 8. Потенціальна енергія електрона всередині металу менше його енергії поза металом на величину . Визначити густину струму термоелектронної емісії, якщо концентрація електронів у металі дорівнює .

Розв’язання. Враховуючи, що енергія вільного електрона в металі менша за його енергію зовні металу на величину роботи виходу , а також припускаючи, що електрони підлягають розподілу Максвелла, густину струму вздовж вісі ОХ (перпендикулярно поверхні металу) запишемо як середнє від за розподілом (1), наведеним у задачі 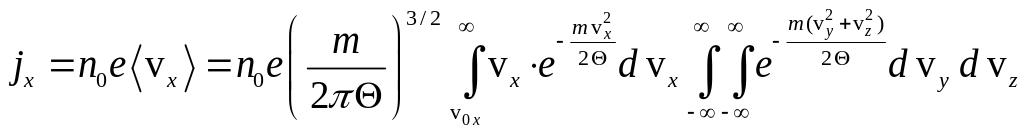1:

, (1)

де швидкість визначається з умови виходу електрона з металу: . Отже, інтегруючи (1), остаточно знаходимо

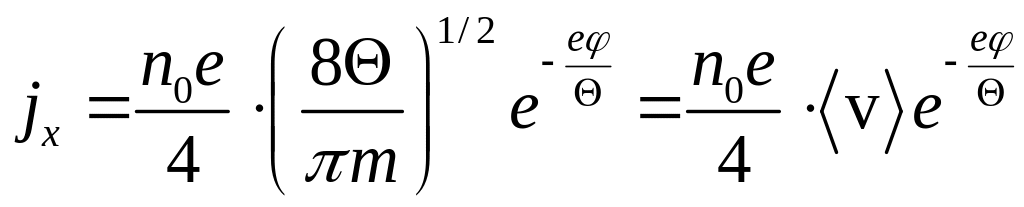, (2)

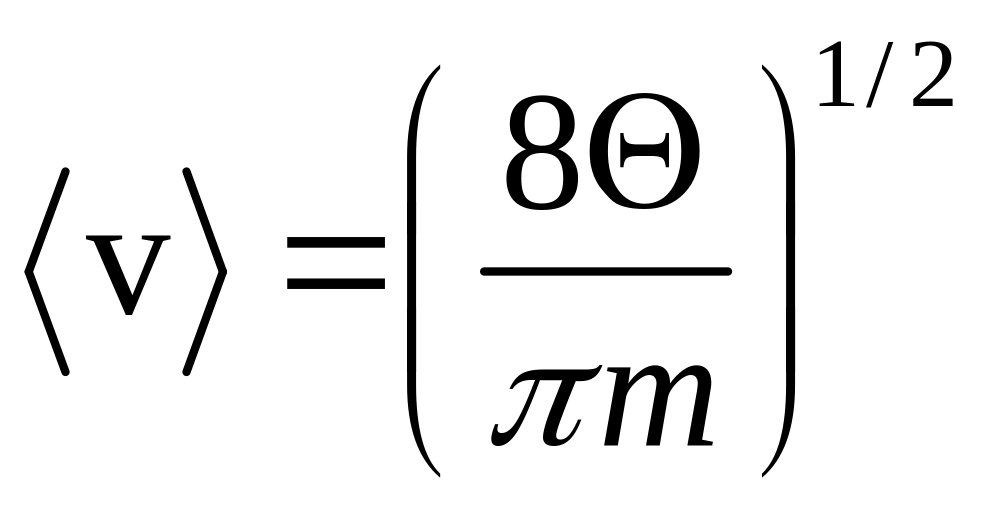
де  середня швидкість електронів за розподілом Максвелла (див. формулу (3) першої задачі). До речі, (2) є класичною формулою Річардсона для густини струму термоелектронної емісії.

Задача 9. Розріджений газ знаходиться в посудині під тиском . Визначити швидкість витікання газу у вакуум через невеликий отвір площею при максвеллівському розподілі молекул газу за швидкостями.

Розв’язання. Ця задача повторює другу частину задачі 4, оскільки повне число молекул, які падають за 1 с на 1 см² стінки (густина потоку ) є таким же їх числом, що виходять з посудини крізь 1 см² отвору за 1 с. Тобто швидкість витікання молекул крізь отвір з перетином дорівнюватиме , де  визначається за формулою (3) задачі 4. Отже, враховуючи, що , остаточно

.