2. Приклади характерних задач з розв’язанням

Задача 1. Визначити значення внутрішньої енергії , що відповідає максимуму канонічного розподілу Гіббса .

Розв’язання. Значення Е_в знайдемо з умови , де – канонічний розподіл Гіббса:

.

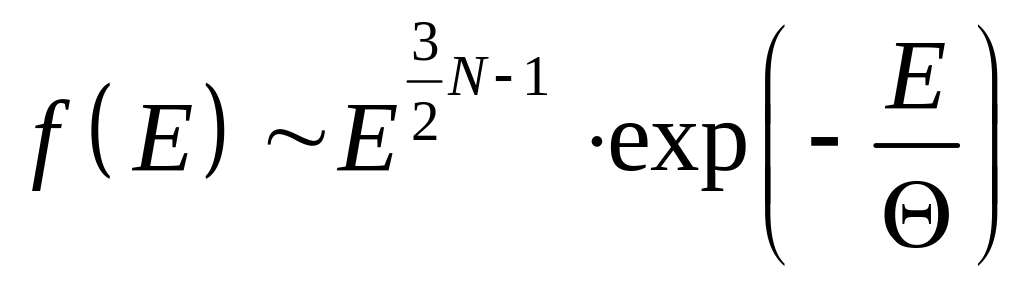Отже,

,

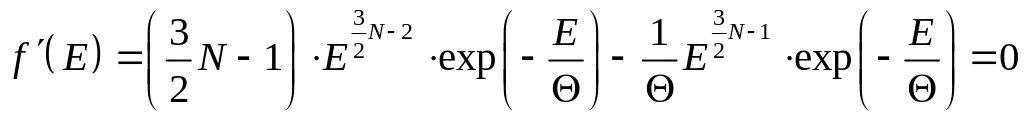звідки

.

Задача 2. Оцінити ширину і відносну ширину канонічного розподілу Гіббса .

Розв’язання. Ширину розподілу можна оцінити як різницю координат точок перегину кривої . Значення та знаходимо з умови , що дає

,

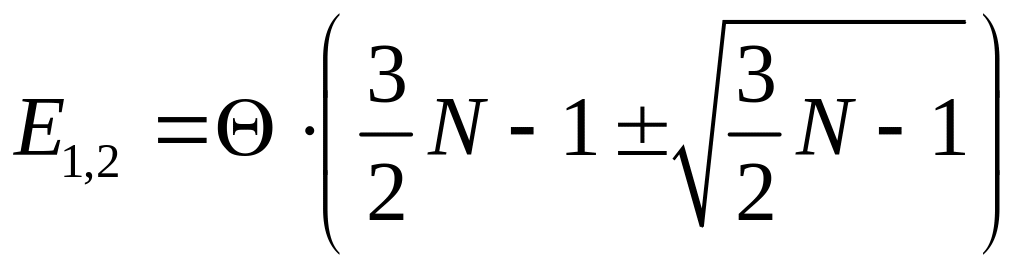звідки

.

Відносну ширину отримаємо, взявши до уваги результат для з попередньої задачі:

.

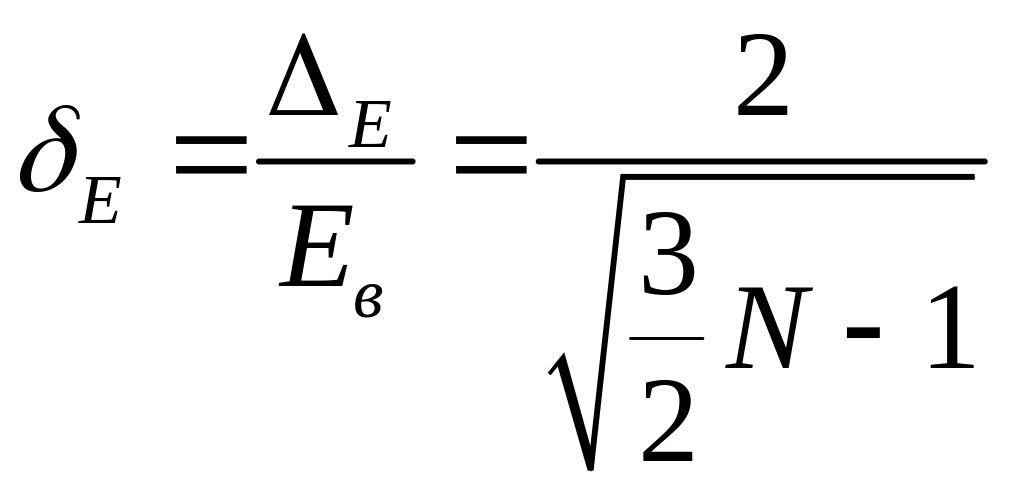Задача 3. Показати, що для будь-якої динамічної змінної системи в термостаті справедливе співвідношення

,

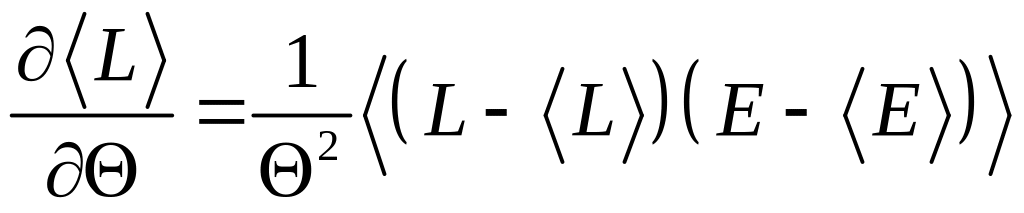де – гамільтоніан системи.

Розв’язання. Середнє значення динамічної змінної системи у термостаті обчислюється за допомогою канонічного розподілу Гіббса :

,

де  гамільтоніан системи,  вільна енергія.

Отже,

. (1)

Враховуючи, що за рівнянням Гіббса-Гельмгольца величина дорівнює термодинамічній внутрішній енергії системи, перепишемо (1) у вигляді:

або

(2)

що й треба було довести, оскільки

.

Задача 4. Виразити термічне і калоричне рівняння стану через конфігураційний інтеграл .

Розв’язання. Термічне та калоричне рівняння стану одержимо на підставі зв’язку вільної енергії та статистичного інтеграла :

. (1)

З термодинаміки відомо, що

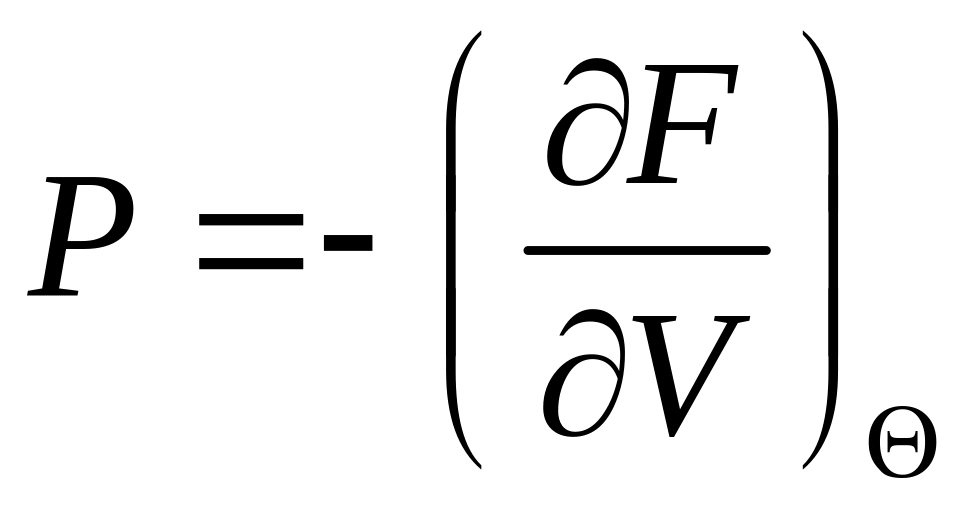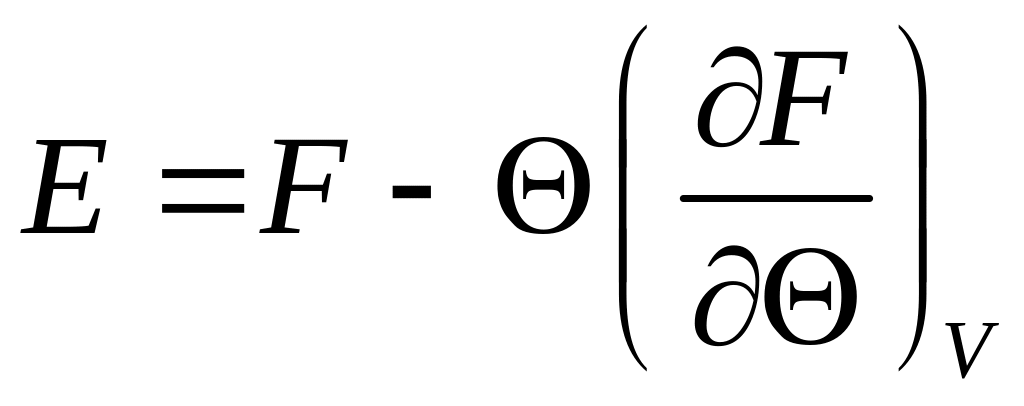, . (2)

Розрахунок в межах канонічного розподілу Гіббса дає

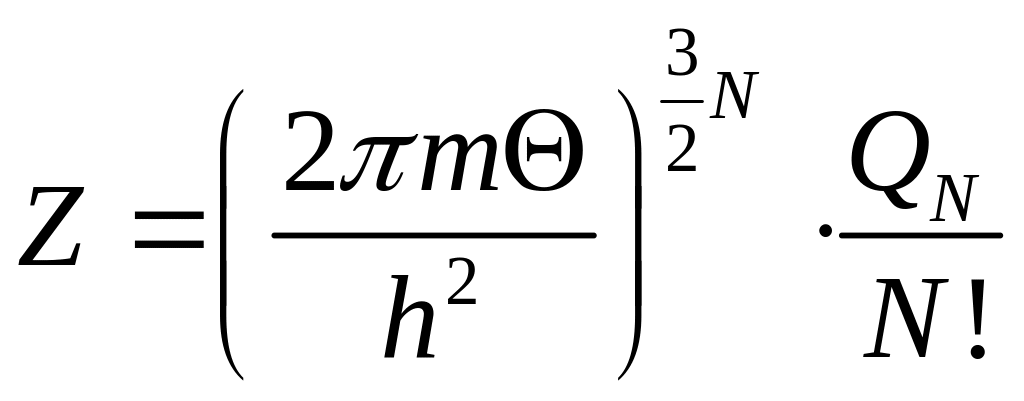, (3)

де  конфігураційний інтеграл, U(q) – потенціальна енергія системи.

Підставляючи (1) у (2) з урахуванням (3), остаточно одержимо шукані рівняння:

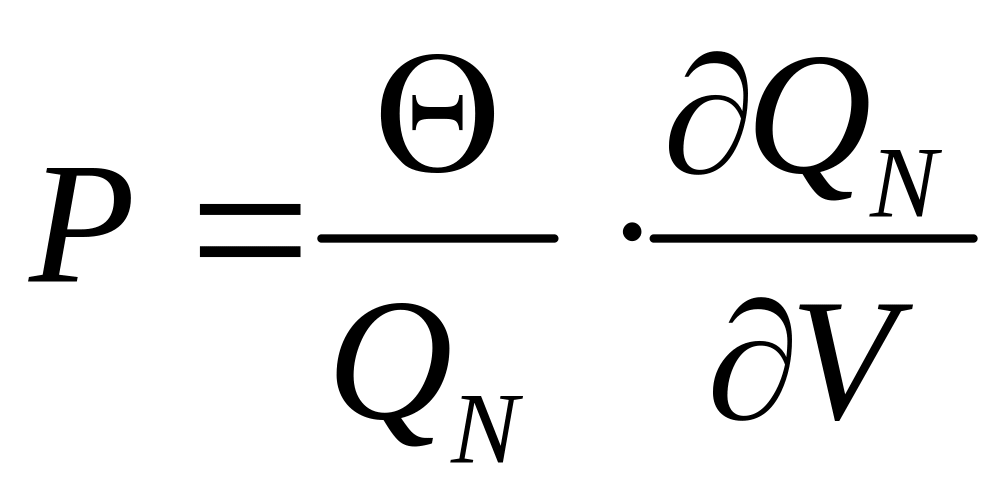
та

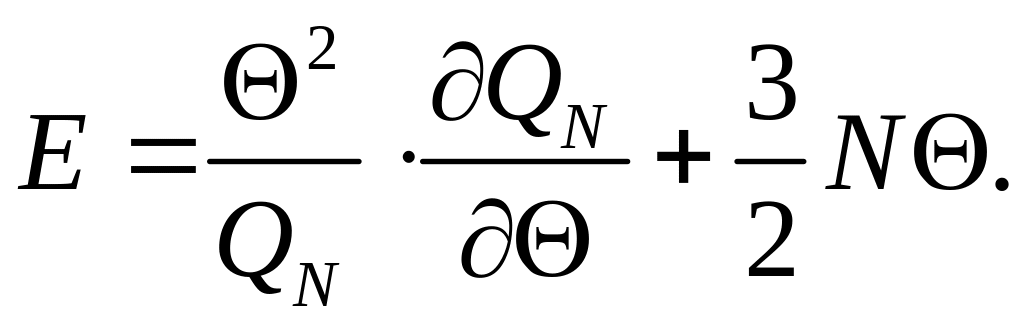
Задача 5. Виразити термодинамічну ентропію через статистичний інтеграл .

Розв’язання. Термодинамічну ентропію можна записати як

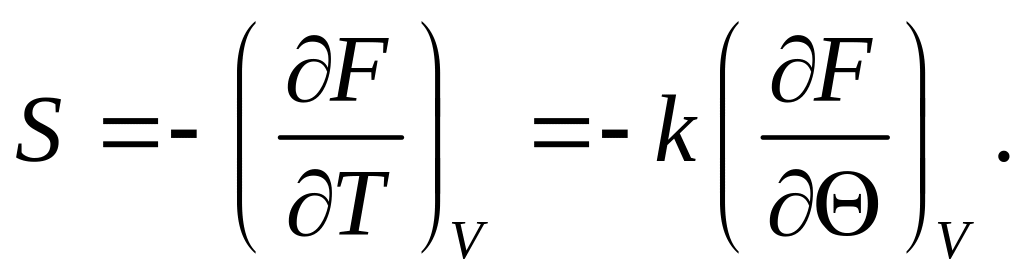(1)

Користуючись формулою (1) попередньої задачі, з (1) одержимо

.

Задача 6. Одержати канонічний розподіл Гіббса за енергіями для лінійного гармонічного осцилятора та обчислити середнє значення його енергії.

Розв’язання. За інваріантністю ймовірності можна записати

звідки для лінійного гармонічного осцилятора

,

де статистичний інтеграл.

Враховуючи формулу (3) задачі 8 з попереднього розділу, маємо та

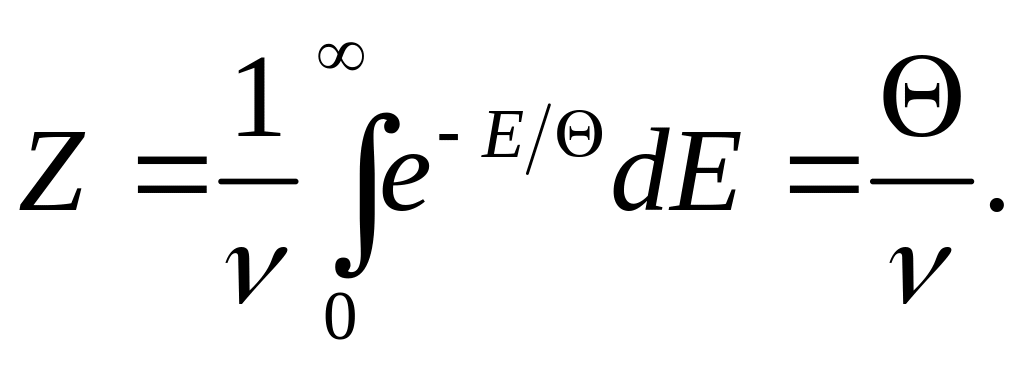
Середнє значення енергії запишемо як

,

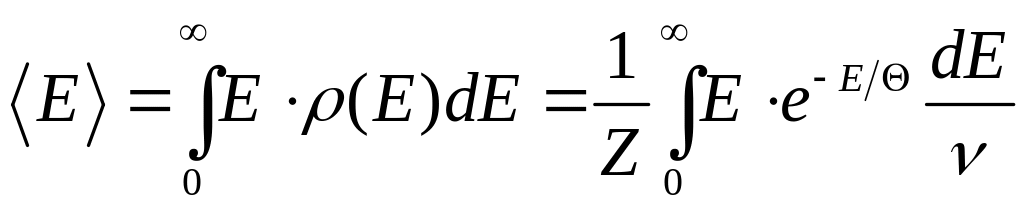що остаточно дає

.

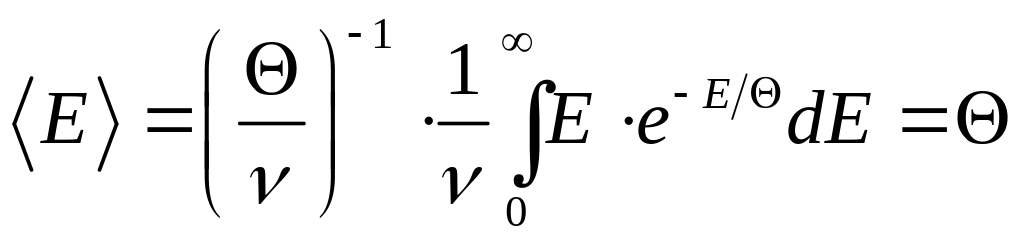Зокрема, цей результат в точності відповідає теоремі про рівнорозподіл кінетичної енергії за ступенями вільності та теоремі про віріал:

.

Задача 7. Знайти статистичний інтеграл , внутрішню енергію і теплоємність ультрарелятивістського газу з законом дисперсії для окремої частинки, де – швидкість світла.

Розв’язання. У межах канонічного розподілу Гіббса статистичний інтеграл для ультрарелятивістськього ідеального газу запишемо як

.

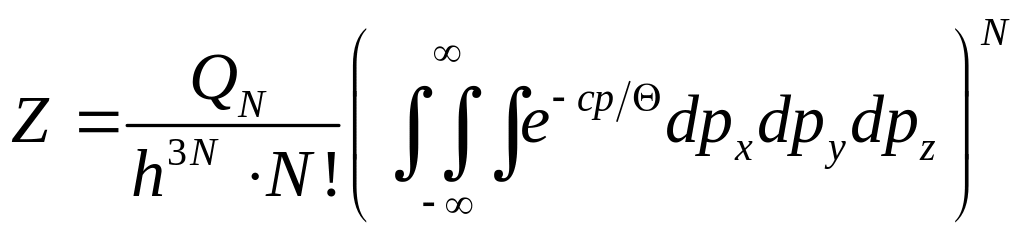Конфігураційний інтеграл ідеального газу дорівнює: . Отже, переходячи до сферичних координат , матимемо

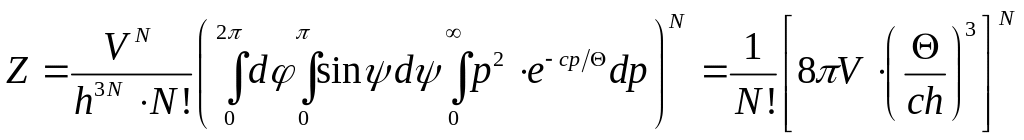. (1)

Внутрішня енергія розраховується через статистичний інтеграл за формулою

. (2)

Тому, підставляючи (1) в (2), остаточно знаходимо:

та

.

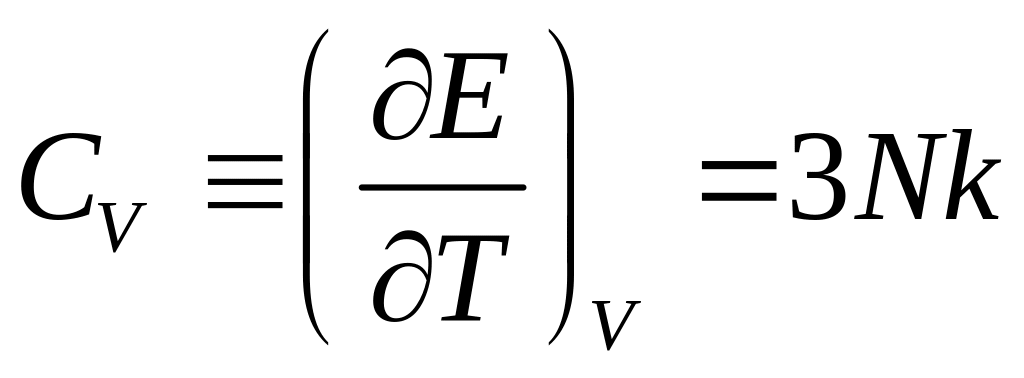Задача 8. Система являє собою стовп висотою і перетином одноатомного ідеального газу з частинок, які знаходяться в однорідному полі тяжіння з напруженістю . Визначити у граничних випадках: , .

Розв’язання. У нашому випадку повна енергія системи має вигляд

,

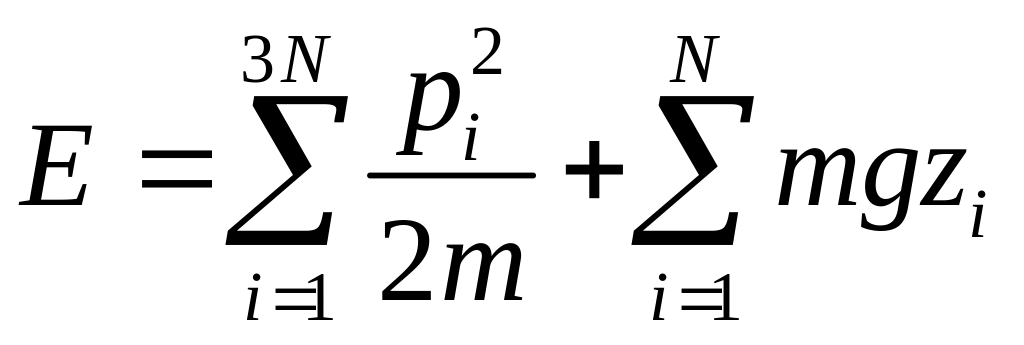де – висота і-ї молекули газу. Для такої системи статистичний інтеграл Z можна записати у вигляді

,

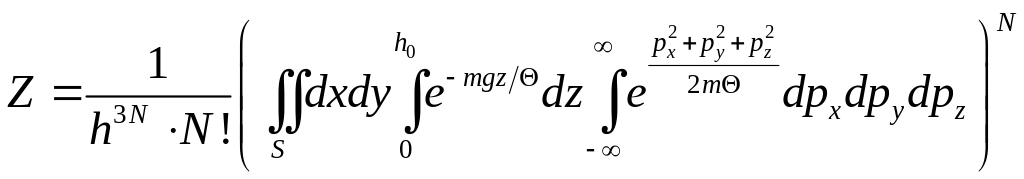що дає

.

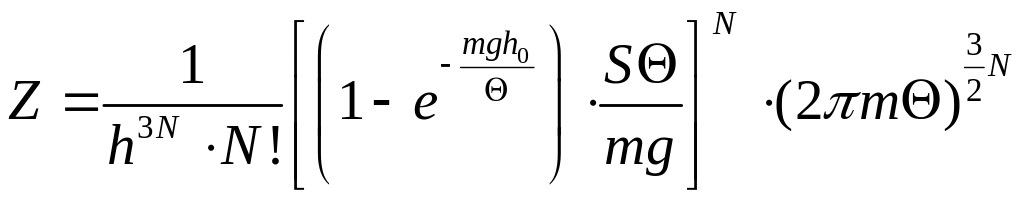Внутрішню енергію системи знаходимо за формулою (2) попередньої задачі:

. (1)

Отже, з (1) маємо

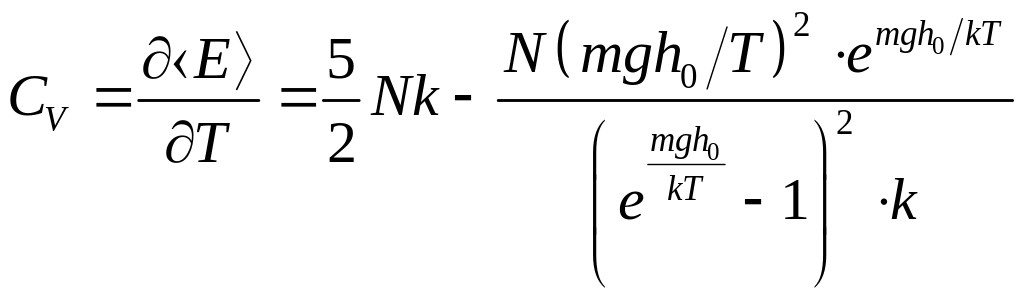. (2)

Математичний аналіз точного результату (2) у граничних випадках дає:

1. при ,

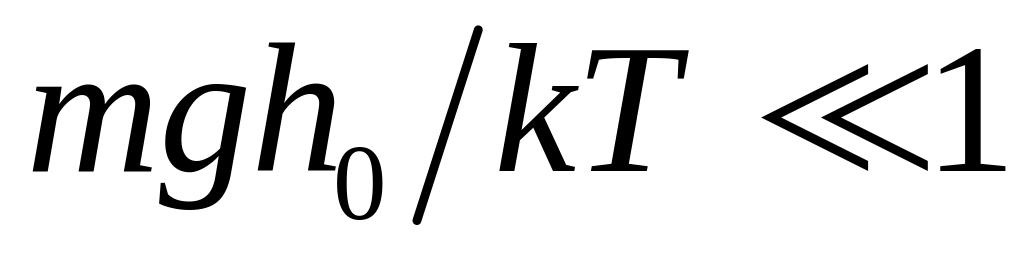
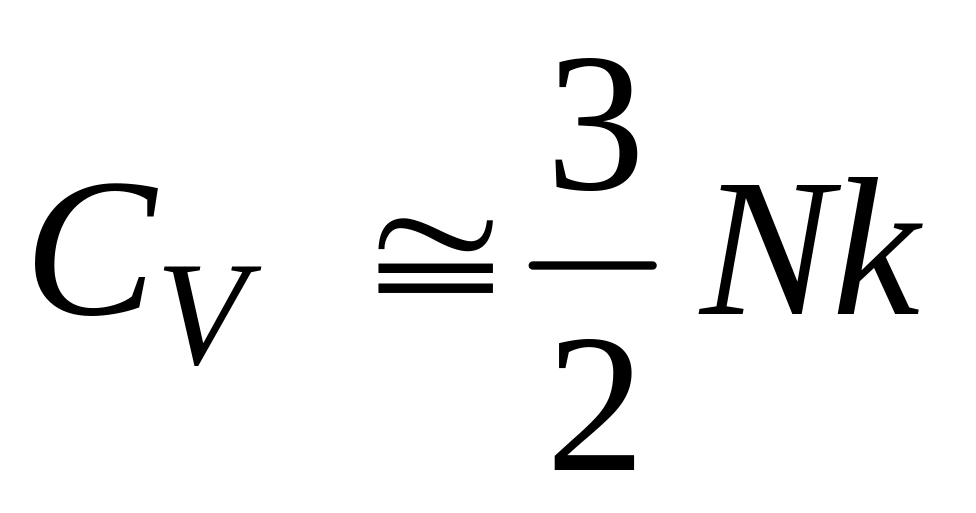2. при .

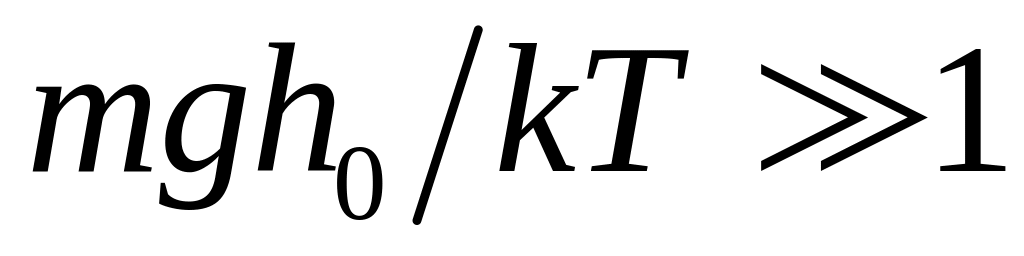
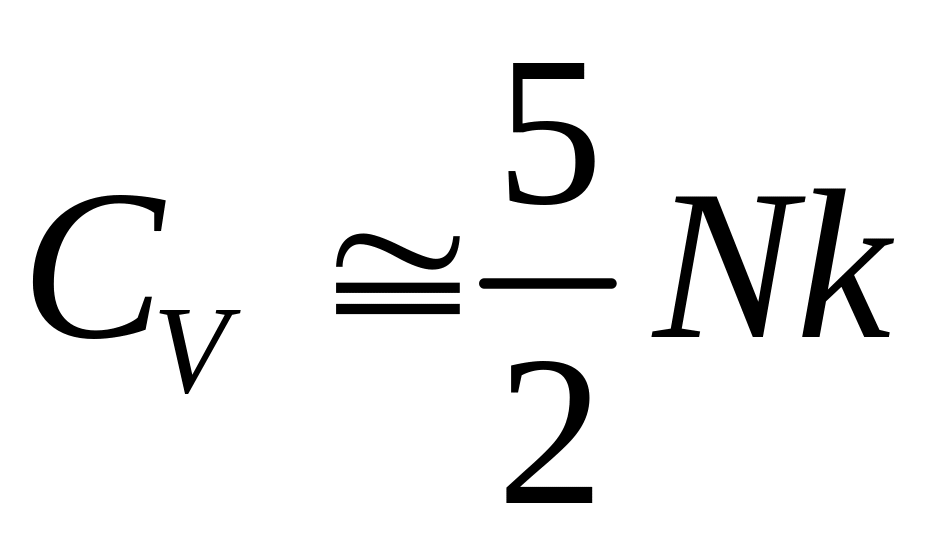Як бачимо, перший граничний випадок призводить до класичного значення для одноатомного ідеального газу у відсутності зовнішнього поля, що зрозуміло, оскільки при цьому припущенні поле тяжіння не впливає на рух частинок системи.

У другому випадку можна було б скористатися теоремою про віріал, що дало б такий самий результат. До речі, у першому випадку ця теорема не працює, оскільки не виконується вимога: при .