2. Приклади характерних задач з розв’язанням

Задача 1. Знайти внутрішню енергію і теплоємність системи невзаємодіючих квантових лінійних гармонічних осциляторів. Дослідити класичну границю.

Розв’язання. Якщо осцилятори не взаємодіють один з одним, енергія системи становитиме , де Е  середня енергія одного осцилятора. Як відомо з квантової теорії, енергетичний спектр квантового лінійного осцилятора є невиродженим і має вигляд , де  квантове число, ν  частота, h  стала Планка. Обчислимо статистичну суму для одного такого осцилятора:

.

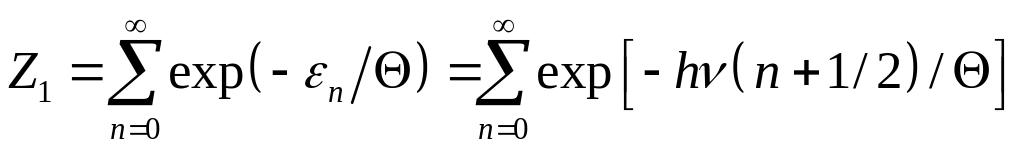Ця сума є сумою нескінченно спадної геометричної прогресії і становить

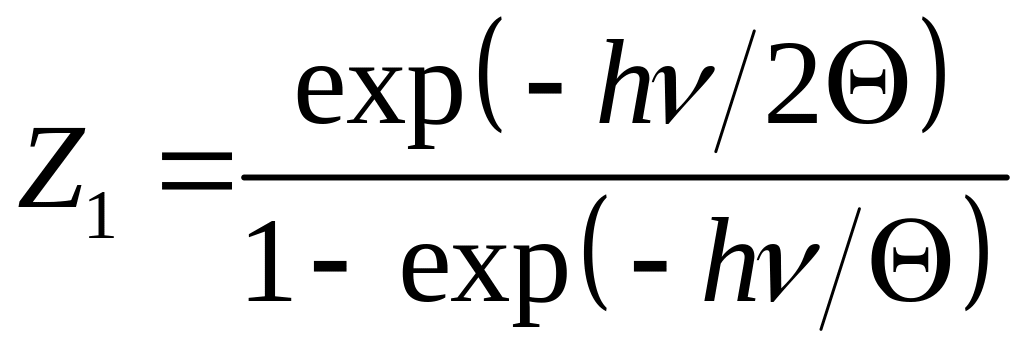. (1)

Середню енергію осцилятора знаходимо за формулою

,

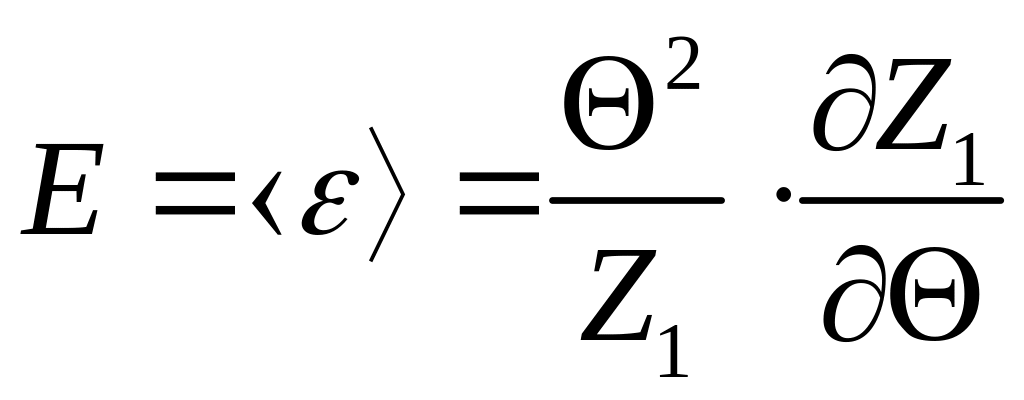що з урахуванням (1) дає

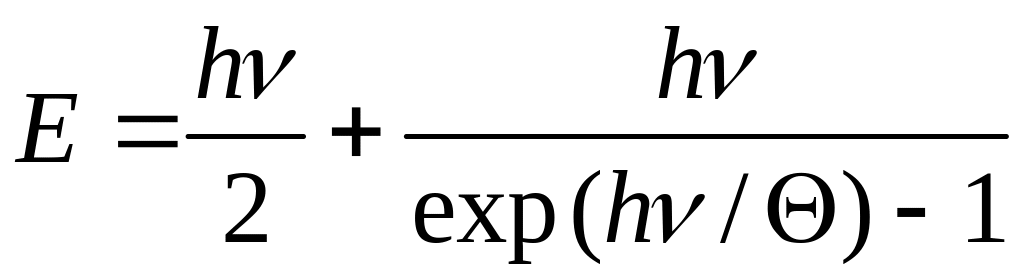. (2)

Класичну границю залежності знайдемо, застосувавши нерівність , що відповідає умові класичності. Отже, розкладаючи за степенями , з (2) одержимо

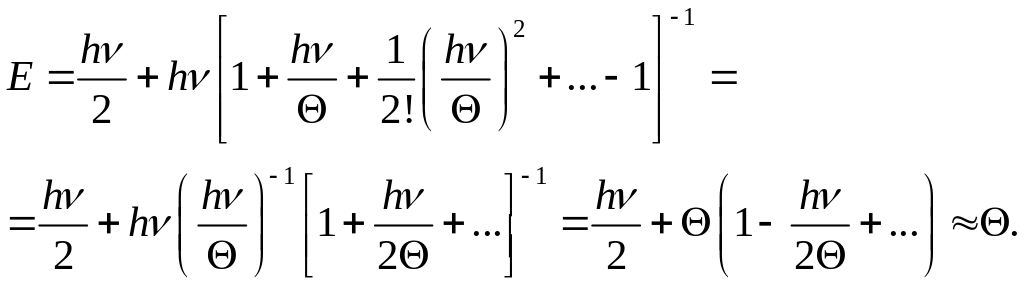
Цей результат відповідає класичній теоремі про рівнорозподіл кінетичної енергії за ступенями вільності та теоремі про віріал, згідно з якими на один ступінь вільності припадає у середньому по як кінетичної, так і потенціальної енергії.

Теплоємність С_V системи в цілому знайдемо з (2) як

,

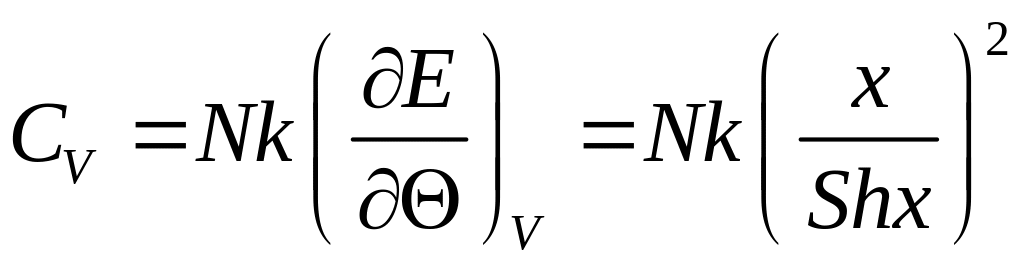де ;  гіперболічний синус.

Задача 2. Визначити теплоємність системи, що складається з незалежних двовимірних гармонічних осциляторів, кожний з яких має -кратно вироджені рівні енергії .

Розв’язання. По-перше, знайдемо середню енергію квантового двовимірного гармонічного осцилятора. Відповідна статистична сума матиме вигляд:

,

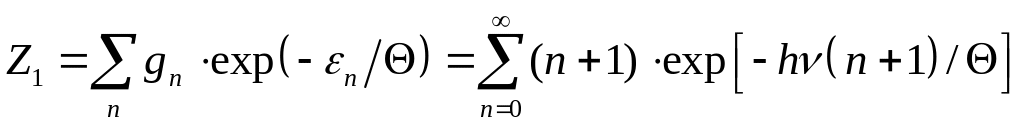що можна переписати як

.

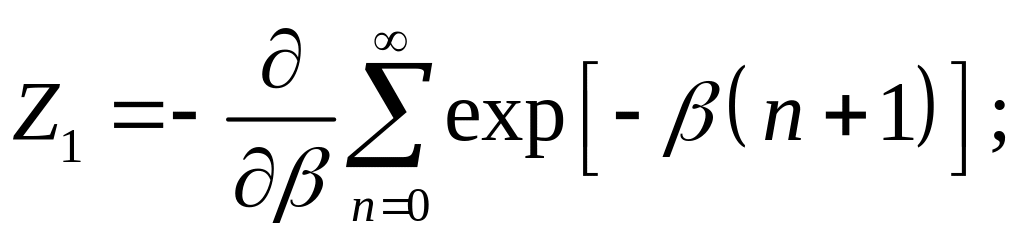
Враховуючи суму нескінченно спадної прогресії, одержимо

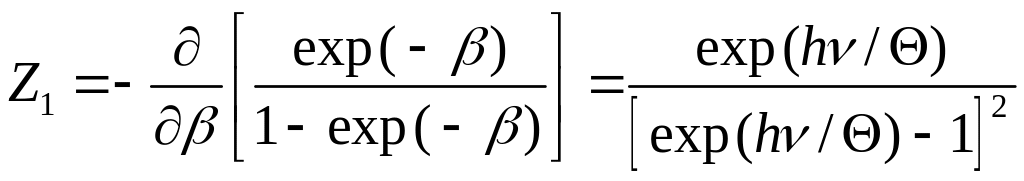. (1)

Далі за формулою

,

використовуючи (1), матимемо

. (2)

Остаточно для всієї системи з (2) знайдемо

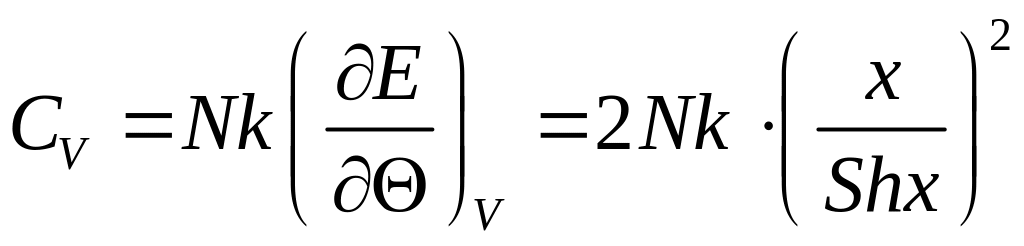, де .

Задача 3. Система має невироджений енергетичний спектр , де . Визначити середню енергію такої системи.

Розв’язання. Застосувавши формулу

; ,

одержимо

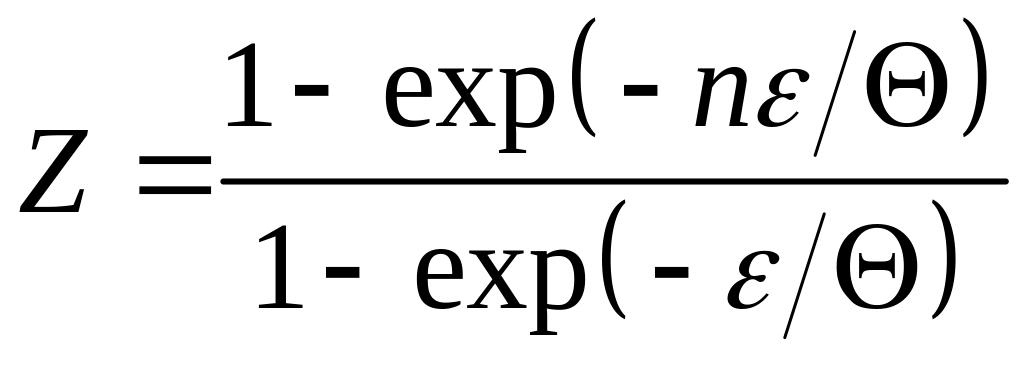. (1)

За формулою

,

використовуючи (1), остаточно одержимо середню енергію системи:

.

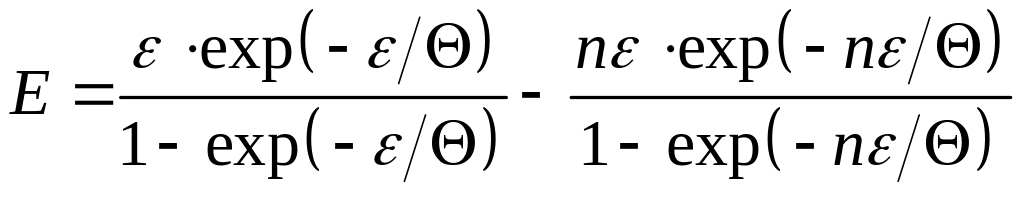Задача 4. Одержати для випадку високих і низьких температур теплоємність системи, що складається з невзаємодіючих двохатомних молекул.

Розв’язання. Двохатомна молекула є квантовим ротатором з енергетичним спектром

,

де  обертальне квантове число,  момент інерції молекули.

Фактор виродження для цього випадку становить , тому для однієї молекули статистична сума має вигляд.

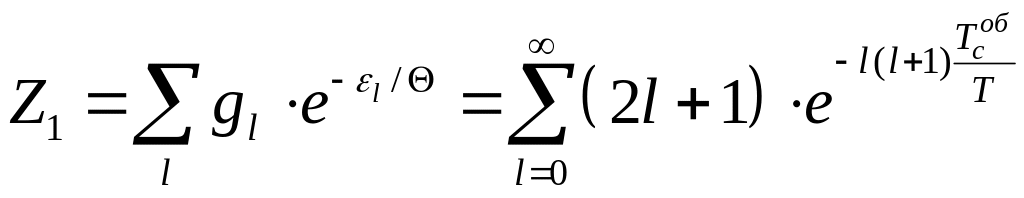, (1)

де  характеристична температура енергії обертання ротатора.

Для високих температур ( ) суму в (1) можна наблизити відповідним інтегралом:

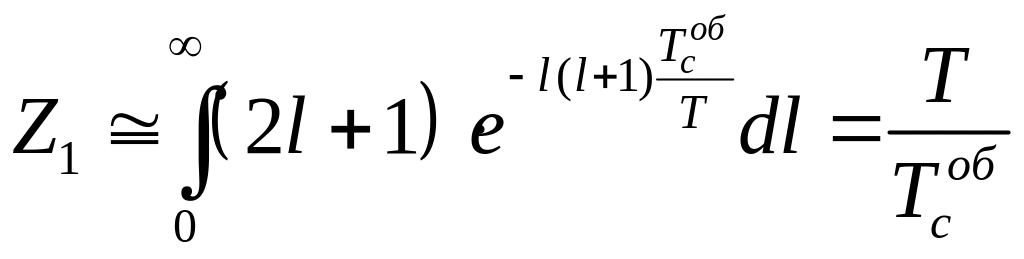. (2)

Застосовуючи формулу

,

для однієї молекули з (2) одержуємо цілком класичний результат: , який відповідає теоремі про рівнорозподіл кінетичної енергії за ступенями вільності. В цьому випадку для системи з N невзаємодіючих молекул маємо обертальну теплоємність

.

У випадку в статистичній сумі (1) можна залишити перші два доданки:

,

що в цьому наближенні дає

.

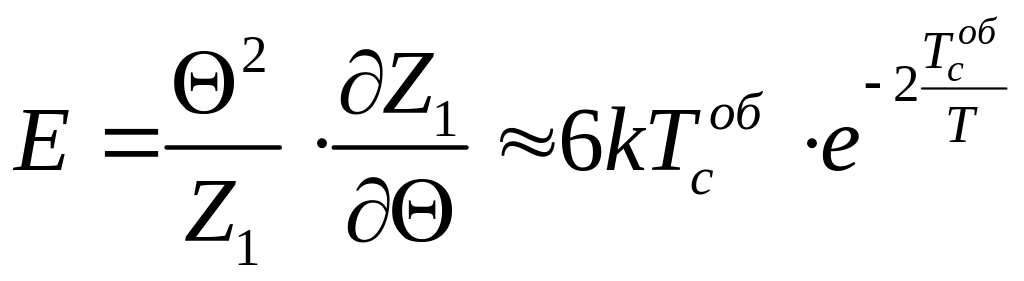Остаточно для всієї системи:

.

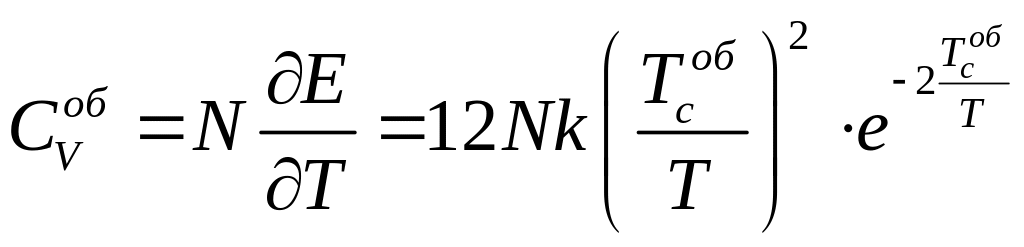Задача 5. Знайти вільну енергію й ентропію системи, що складається з квантових ротаторів при .

Розв’язання. Для вільної енергії одного ротатора застосовуємо зв’язок зі статистичною сумою :

,

де у випадку беремо з формули (2) попередньої задачі. Таким чином, для N ротаторів маємо

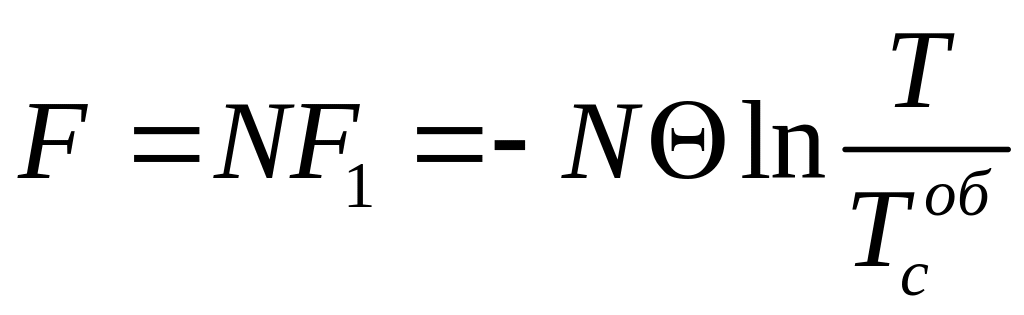. (1)

Ентропію S всієї системи знаходимо з урахуванням (1) у вигляді

.

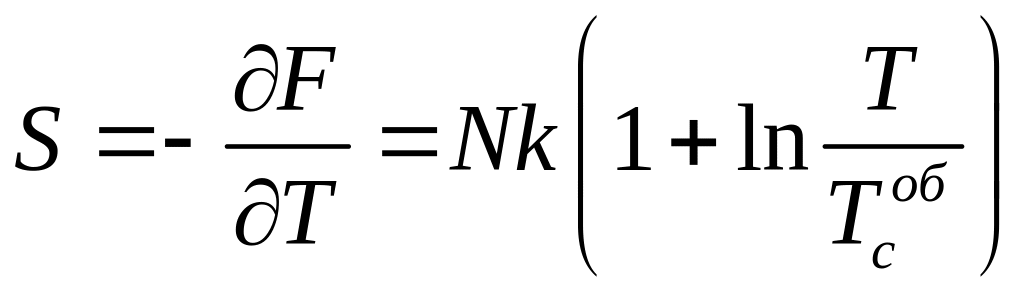Задача 6. Яке рівноважне відношення концентрацій орто- і параводню при температурі .

Розв’язання. Рівноважне співвідношення орто- та параводнів в природному водні становить ~ 3:1 (в орто- та параводні спіни протонів відповідно паралельні та антипаралельні). Тому відношення концентрацій через відповідні статистичні суми можна записати у вигляді

.

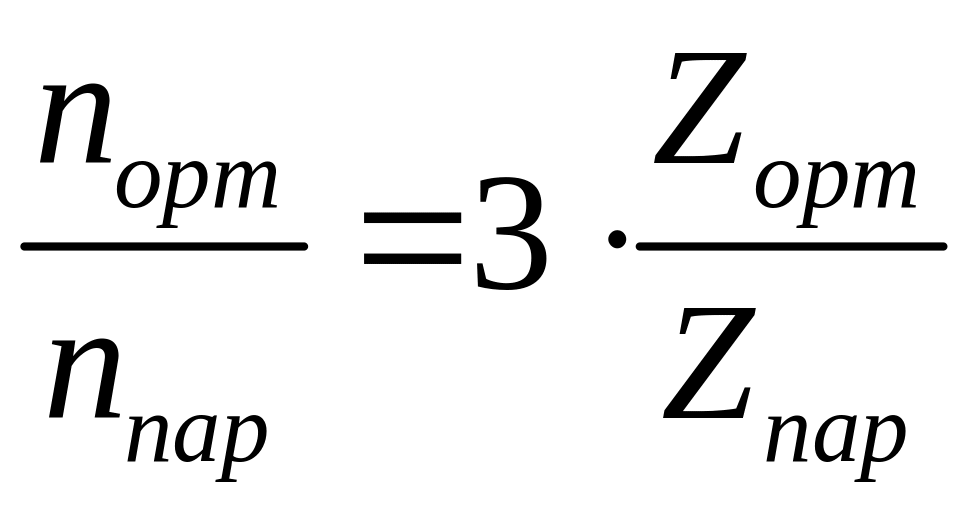З квантової механіки відомо, що параводень, як ротатор, може перебувати лише в станах з парними значеннями обертального квантового числа , а ортоводень  з непарними. Тобто шукане співвідношення становитиме

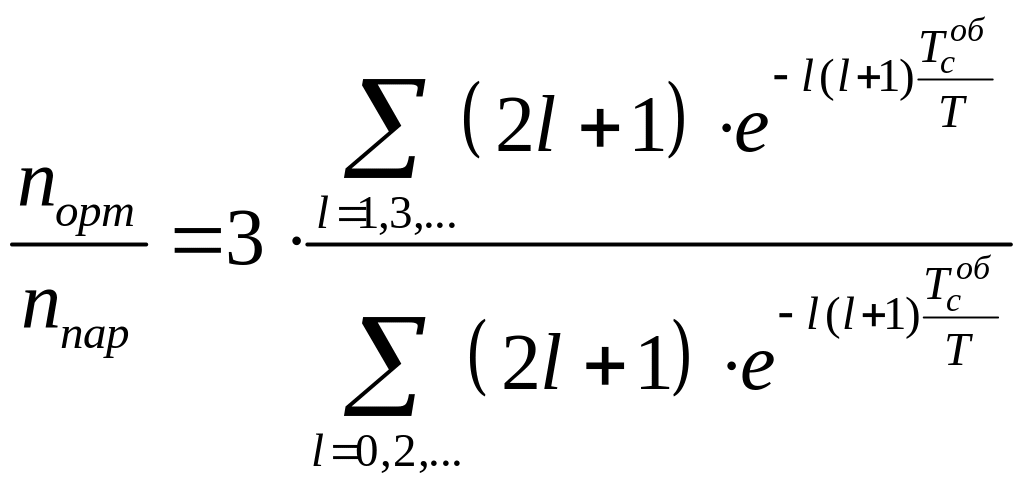. (1)

Для випадку , залишивши в сумах (1) лише перші доданки, остаточно одержимо

.

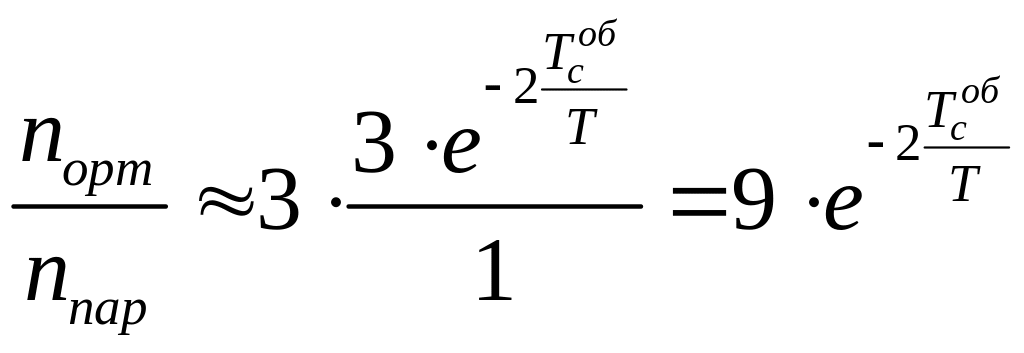Задача 7. Обчислити молярну теплоємність алмазу при Т = 100 К. Температура Дебая Т_D = 1843 К.

Розв’язання. Внутрішня енергія одного моля твердого тіла за теорією Дебая становить

, (1)

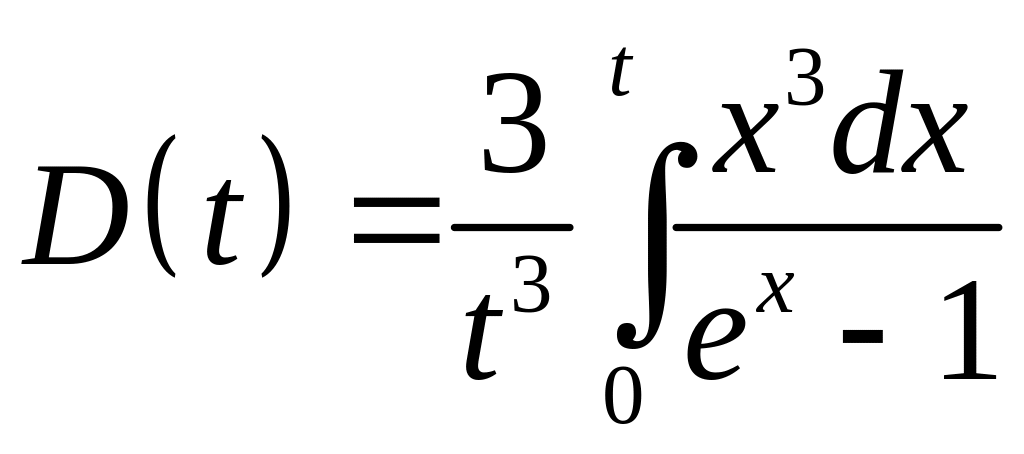
де  функція Дебая;

 нульова енергія, яка не залежить від температури;

, T_D  характеристична температура, яка залежить від структури твердого тіла.

В нашому випадку , тому функцію Дебая наближено можна розглянути у вигляді

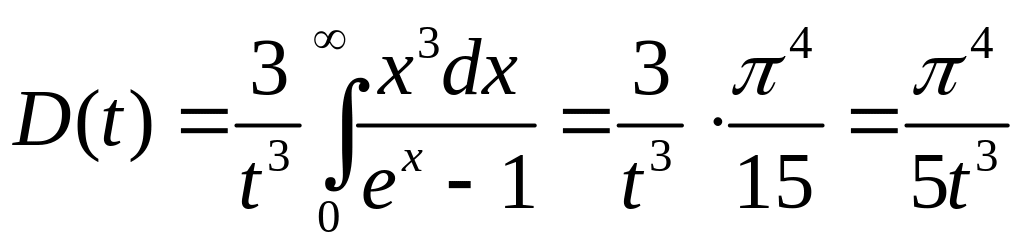. (2)

Підставляючи (2) в (1), остаточно знаходимо молярну теплоємність алмазу:

.
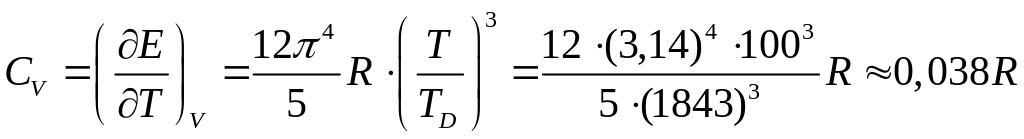