Пороговые значения r и r2 при 90 % уровне доверия

N	r	r2	N	r	r2
10	0,46	0,21	30	0,29	0,08
15	0,39	0,15	70	0,19	0,04
20	0,34	0,12	80	0,18	0,03
25	0,31	0,10	90	0,16	0,03

Если расчетный коэффициент корреляции будет больше табличного для данного объема наблюдений, то с вероятностью 0,9 можно утверждать, что есть связь между показателями.

Например, в нашем примере r_р = 0,6, число наблюдений N = 30; r_табл. = 0,29, то есть связь между показателями.

Коэффициент корреляции в квадрате (r²) называется коэффициентом детерминации и показывает долю изменений Y за счет Х. В нашем примере эта доля составляет 36 %. В программе Excel этот показатель обозначается большими буквами R^2..

Чтобы решить модель с помощью программы Excel, надо построить график, на любой точке графика исходных данных правой стороны мышки кликнуть «Показать уравнение тренда», выбрать нужную модель ( линейную, степенную или логарифмическую), внизу таблицы поставить две галочки в квадрат ах- показать параметры уравнеия и коэффициент апроксимации.

1.3. Оценка модели. Заполняем табл.3 и определяем:

1) расчетные значения зависимой переменной по найденной модели (например, Yp = - 9,52 + 1,2823*Х) путем подстановки в полученную модель фактических значений объемов производства (Х), если расчеты сделаны правильно, то Y = Y_р;

2) ошибки модели е и е² (е = Y - Yp;

3) надежность модели:

− с помощью коэффициента вариации:

V = .

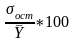_где σ_ост = _;

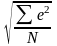=Уср = ;

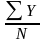если коэффициент вариации будет меньше 5 - 10 процентов, то модель можно использовать на практике;

− с помощью средней процентной ошибки МРЕ =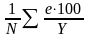 =(1/N)*Σ1;

− с помощью средней абсолютной процентной ошибки

МАРЕ = = (1/N)*Σ2, для этого вычисляем Σ1 и Σ2 (кол.7 и 8).

Таблица 3

Исходные данные и расчеты

Исходные данные			Оценка линейной модели
наб.	У	Х		Ур	е	е2	е*100/У	ABS =|е|*100/У
1	2	3		4	5	6	7	8
1	10,5	16,2		11,3	-0,8	0,64	- 7,62	7,62
2	..	..		..	..	..	…
30	14,6	18,2		13,8	0,8	0,64	5,48	5,48
Σ	Σ	Σ		Σ	Σ	Σ	Σ1	Σ2

Если МРЕ и МАРЕ меньше 5 %, то расхождение между Y и Yp несущественное и расчетное значение будет отличаться от фактического в 5 % из 100 случаев.

Такие же расчеты необходимо сделать по другим моделям

2. Дать рекомендации по использованию моделей.

Для этого заполнить табл. 4.

Таблица 4

Результаты расчетов по моделям

Название модели	Уравнение	R2	V	МРЕ	МАРЕ
линейная
степенная
логарифмическая

Проанализировав результаты расчетов, необходимо сделать экономико-математические выводы и записать принимаемое уравнение для анализа зависимости расхода воды от объема производства.

Исходные данные к остальным лабораторным работам приведены в табл. 5. К каждому заданию надо составить таблицу исходных данных, используя нужную информацию из табл. 5.

Таблица 5