2.1.5. Косоугольное вращение
При использовании косоугольного (коррелированного) вращения большинство показателей ортогонального вращения сохраняется, но к ним добавляются еще и новые (список дополнительных матриц, используемых только для косоугольного вращения, см. в табл. 1).
При косоугольном вращении для выделения факторной структуры вместо матрицы факторных нагрузок используется матрица факторного отображения. Квадраты значений в матрице факторного отображения представляют собой характерный вклад каждого фактора в дисперсию каждой переменной, исключая часть дисперсии, возникающей как следствие корреляции факторов между собой. Для нашего примера матрица факторного отображения после косоугольного вращения имеет вид:
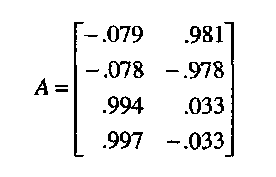
Характерный вклад первого фактора в переменную стоимость путевки равен (—.079)2, в переменную комфортабельность комплекса (-.078)а, в переменную температура воздуха (.994)2 и в переменную температура воды (.997)2.
Коэффициенты факторных значений вычисляются аналогично:
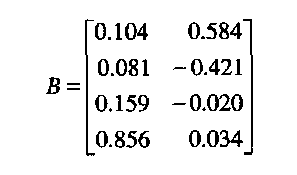
Применяя уравнение (17), получаем значения факторов:
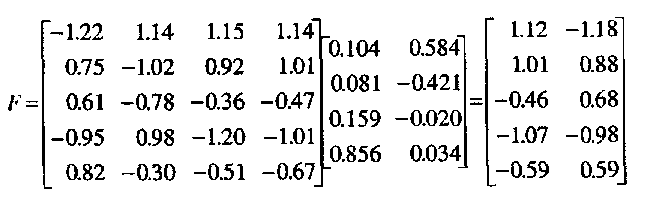
Определив значения факторов, можно посчитать корреляции между факторами. Для этого применяется уравнение:
Ф=(1/N-1)F’F, (19)
т.е. один из способов вычисления корреляций между факторами состоит в делении произведения матрицы стандартизированных значений факторов и транспонированной ей на количество наблюдений минус один.
Факторная корреляционная матрица является стандартной частью компьютерной распечатки после выполнения косоугольного вращения. Например:
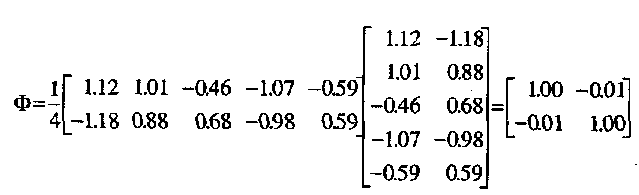
Взаимосвязь между первым и вторым факторами очень мала (-.01), т.е. в рассматриваемом примере факторы практически никак не связаны.
При косоугольном вращении матрица взаимосвязей между переменными и факторами называется структурной матрицей. Она включает как характерную взаимосвязь между переменной и фактором (из матрицы факторного отображения), так и взаимосвязь между переменной и дисперсией, полученной за счет наложения факторов друг на друга. Структурную матрицу можно получить из уравнения:
S=AФ, (20)
т.е. структурная матрица — это произведение матрицы факторного отображения и матрицы корреляции факторов.
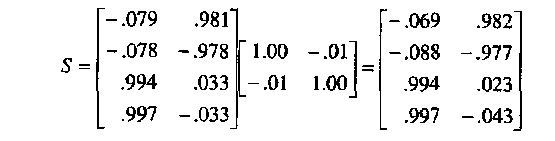
Переменные стоимость путевки, комфортабельность комплекса, температура воздуха, температура воды имеют коэффициенты корреляции с первым фактором: -.069, -.088, .994 и .997; со вторым: .982, -.977, .023 и -.043.
Дискутируется вопрос, следует ли интерпретировать матрицу факторного отображения или структурную матрицу после косоугольного вращения. Преимущество структурной матрицы заключается в том, что ее легче понять. Однако взаимосвязи переменных и факторов сильно зависят от любых наложений факторов друг на друга. По мере увеличения взаимосвязей между факторами становится все сложнее определить, какая же из переменных относится к тому или иному фактору. С другой стороны, матрица факторного отображения содержит величины, представляющие характерные вклады каждого фактора в дисперсии переменных. Смешанная дисперсия не учитывается, но здесь проще выделить переменные, описывающие фактор. Однако если факторы высоко коррелирует друг с другом, то может оказаться, что к ним нельзя отнести ни одну из переменных, поскольку после того, как будут исключены наложения факторов, практически не останется ни одной характерной дисперсии.
Как правило, исследователи интерпретируют и включают в свои отчеты матрицу факторного отображения, а не структурную. Однако заинтересованный читатель, зная матрицу корреляций факторов Ф, а также одну из двух матриц — факторного отображения или структурную, всегда может вычислить другую используя уравнение (20).
После косоугольного вращения матрица R получается следующим образом:
R=SA’ (21)
т.е. воспроизведенная матрица взаимосвязей — это произведение структурной матрицы и транспонированной матрицы факторного отображения. Воспроизведенная матрица взаимосвязей позволяет вычислить остаточную матрицу взаимосвязей с помощью уравнения (15) и оценить адекватность результатов факторного анализа.