2.1.4. Факторные значения

После вычисления матрицы факторных нагрузок можно вычислить значения факторов для каждого наблюдения (испытуемого). Приведем наиболее распространенный способ вычисления факторных значений. Сначала вычисляются коэффициенты регрессии, позволяющие на основе значений переменных для каждого респондента оценить для него значения факторов. Пусть R^-1 — матрица, обратная матрице взаимосвязей, а А — матрица факторных нагрузок, тогда матрица коэффициентов факторных значений В вычисляется по формуле:

B= R^-1 A, (16)

т.е. коэффициенты для определения факторных значений являются результатом умножения матрицы, обратной матрице взаимосвязей, на матрицу факторных нагрузок.

В нашем примере⁸:

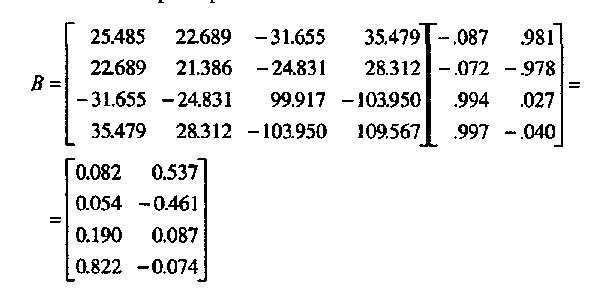
Для определения факторных значений респондентов по первому фактору все их значения по переменным стандартизируются, а затем суммируются с учетом весов (веса равны соответствующим числам из матрицы В). Например, суммируются весовые коэффициенты для стоимости путевки (0,082), для комфортабельности комплекса (0,054), для температуры воздуха (0,190) и для температуры воды (0,822). В матричной форме это выглядит так:

F=ZB, (17)

т.е. значения факторов равны произведению стандартизированных значений по переменным и матрицы коэффициентов значений факторов.

В нашем примере:

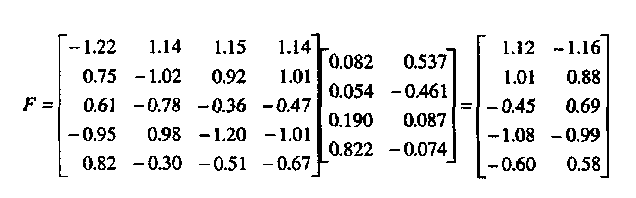
Первый респондент по первому фактору получил стандартизированное значение 1.12, а по второму он получил —1.16. Таким образом, этот респондент имеет очень высокие положительные значения по униполярному «климатическому» фактору, а очень высокое отрицательное значение по «экономическому» фактору свидетельствует о том, что для него комфортность отдыха существенно важнее, чем его низкая стоимость. Второй респондент имеет высокое значение по «климатическому» фактору (но все-таки меньшее, чем у первого респондента) и высокое положительное значение по «экономическому» фактору. Следовательно, у него соображения экономии существенно превалируют над соображениями комфорта. Третьего респондента климатические условия не волнуют, но, выбирая место отдыха, он будет в первую очередь ориентироваться на его дешевизну. И т.д. Среднее стандартизированных течений всех испытуемых по каждому фактору равно нулю.

Также можно воспроизвести значения по переменным, исходя из значений факторов. Для этого используется следующее уравнение:

Z=FA’, (18)

т.е. матрица воспроизведенных стандартизированных значений по переменным вычисляется как произведение матрицы значений факторов и транспонированной матрицы факторных нагрузок.

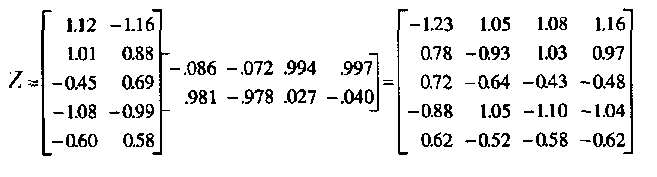
Первый респондент (первая строка в матрице Z) теоретически (прогнозируемо) должен иметь стандартизированное значение -1.23 по стоимости путевки, 1.05 по комфортабельности комплекса, 1.08 по температуре воздуха и 1.16 по температуре воды. Если в ходе факторного анализа действительно удалось уловить существующие взаимосвязи между переменными и их структуру, то расчетные величины в этой и вычисляемой матрицах взаимосвязей близки к наблюдаемым (полученным экспериментально) величинам.

В качестве упражнения рекомендуем выписать все эти формулы для получения расчетных значений по переменным. Например, для первого респондента:

-1,23 =-,086 (1,12)+ ,981 (-1,16)

1,05 = -,072 (1,12)- ,978 (-1,16)

1,08 = ,994 (1,12)+,027 (-1,16)

1,16 = ,997 (1,12)- ,040 (-1,16),

Или в алгебраической форме:

Z стоимости путевки=а₁₁F1 + а₁₂F₂

Z комфортабельности комплекса=а₂₁F1+а₂₂F₂

Z температуры воздуха=а₃₁F₁ + а₃₂F₂

Z температуры воды = а₄₁F₁ + а₄₂F₂

Таким образом, в ходе исследования принимается гипотеза о том, что общая латентная структура факторов характеризует всех испытуемых, однако каждый из них имеет различные показатели (факторные значения) по каждому из факторов. Каждый конкретный показатель испытуемого по наблюдаемой переменной вычисляется как линейная комбинация показателей (факторных значений) испытуемого по базисным факторам.