3.7. Сравнение факторных решений и выборок
Часто исследователю бывает необходимо определить, одинаковы или нет две факторные структуры, полученные на основе анализа двух различных (по опыту или по каким-то другим характеристикам) выборок. Для сравнения факторных решений используют матрицу факторного отображения, содержащую корреляции между переменными и факторами, или матрицу факторного отображения с учетом значимости корреляций между ними. Руммель (Rummel, 1970), Левайн (Levine, 1977) и Горсуч (Gorsuch, 1983) приводят хорошие обзоры методов сравнения факторных решений. Мы ограничимся способами, описанными у Хармана (1972).
Первый способ можно назвать качественным. Допустим, получены две факторные структуры — два набора факторов f и k с матрицами факторного отображения А и B соответственно. Задача состоит в нахождении и оценке такой матрицы Т, что:
АТ=В. (24)
Отношение между факторами задается с помощью этой же матрицы:
ƒ=Tk. (25)
Используя это последнее соотношение, можно проанализировать вклад факторов из набора k в дисперсию любого из факторов набора f.
Чтобы найти матрицу Т, нужно воспользоваться следующим соотношением: (А’А)-1(А’А)=Е — единичная матрица. Тогда, умножив слева и справа части равенства (24) на (А’А)-1А’, получим:
Т=(А’А)-1А’В. (26)
Другой способ связан с вычислением «коэффициента конгруэнтности» (Такер), «коэффициента несовпадения» (Барт) или «степени подобия факторов» (Рили и Нейгауз). Все коэффициенты аналогичны.
Перед задачей сопоставления факторов исследователь может оказаться в двух случаях. Первый: есть фиксированный набор параметров, измеренных на различных выборках, и нужно определить степень соответствия факторов. Второй: выборка фиксирована, а параметры могли быть различны.
Будем обозначать элементы матрицы факторных нагрузок kaij, а элементы матрицы значений факторов kzli, где k — номер сравниваемой факторной структуры, i изменяется от 1 до n (количество переменных), l - от 1 до N (количество респондентов), j — номер фактора. Для простоты будем считать, что нам надо сравнить две факторные структуры, поэтому k=l,2. Тогда коэффициент конгруэнтности для факторов р и q в первом случае можно записать так:
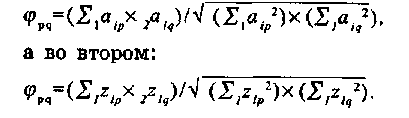
Значение коэффициента конгруэнтности меняется от +1 при полном совпадении (или —1 при полном обратном совпадении) до нуля при полном отсутствии связи.
Если m1 и m2 — количества факторов в двух исследованиях, то можно вычислить m1m2 коэффициентов конгруэнтности, характеризующих степень подобия двух систем факторов. Будем говорить, что данный фактор из одного исследования конгруэнтен некоторому фактору из другого исследования, если им соответствует достаточно большое значение коэффициента φ. В частности там, где это не вызовет недоразумений, Рили и Нейгауз предлагают объединять факторы в пары таким образом, чтобы значение коэффициента φ для каждой пары было максимально возможным.
В настоящее время проверкой теорий и сравнением факторных решений, полученных на различных выборках, занимается относительно новая область многомерной статистики — структурное моделирование (латентно-структурный анализ).