§4.6. Мощности в цепи синусоидального напряжения.
1) Мгновенная мощность:
= =
= [BA] – вольт-ампер
2) Активная мощность (средняя за период):
= [Bт]
из ∆-ка напряжений (послед.):
из ∆-ка токов ():
3) Реактивная мощность: [BAp]
из ∆-ка напряжений (послед.):
из ∆-ка токов ():
4) Полная мощность: [BA]
∆-к
мощностей:
;
- коэффициент мощности.
Желательно, чтобы , так как при этом уменьшаются потери электроэнергии в проводах.
§4.7. Символический метод расчета электрических цепей.
(Метод комплексных амплитуд)
Используется для расчета сложных электрических цепей алгебраически (~ - тильда).
- комплекс мгновенного значения напряжения.
В символическом методе синусоидальная функция заменяется ее символом комплексной функции.
⊜ , где
- комплексная амплитуда (комплексное число).
⊜
Комплексную функцию можно отобразить на комплексной плоскости в виде радиус-вектора:
– оператор
поворота.
Умножение на означает поворот вектора на угол против часовой стрелки.
При выполнении линейных операций над гармоническими функциями в символической форме ( +, , умножение на const, дифференцирование и интегрирование) оказывается общим множителем и при выполнении расчетов его можно отбросить и работать только с комплексными числами. Затем
приписывается к результату.
4.7.1. Дифференцирование и интегрирование гармонических функций в символической форме.
, где
1)
2)
4.7.2. Последовательное соединение r, l, c – элементов. Расчет символическим методом.
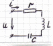
Дано: ; , L, C .
Определить:
⇒ 𝜑 - ?
По 2зК: (1)
Заменим и соответствующими комплексами:
1) , где
2)
Тогда 3)
4)
5)
=
(2) -
– комплексное сопротивление цепи.
;
Решение задачи: =
Построим векторную диаграмму в комплексной плоскости:
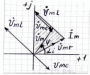∆-к
напряжения
1)
2)
3)
Умножение вектора на означает его поворот на против часовой стрелки.
4) ⊜
⊜
4.7.3. Параллельное соединение r, l, c.
Дано: ; , L, C .
Определить:
⇒ 𝜑 - ?
Решение:
1) по 1зК: (1)
2) Заменяем мгновенные значения токов и напряжений соответствующими комплексами
; , где ,
Тогда,
,
где и
= (2)
=
= (3) -
𝒴 - комплексная проводимость цепи.
или - закон Ома
,
где 𝜑 – аргумент , |𝒴| - модуль,
, где - полная проводимость
По закону Ома находим :
=
4.7.4. Эквивалентные участки цепи.
= =
= =
1) 𝒴→Z ; =
где ;
2) Z → 𝒴 ; аналогично
4.7.5. Законы Ома и Кирхгофа в символической форме.
1) 1з.Ома (уже выводился):
, где - при последовательном соединении
, где - при параллельном соединении
- при включенном ЭДС
2) Законы Кирхгофа
1зК: , где
2зК: , где
- токи для действительных значений
Правило знаков такое же, как в цепи постоянного тока.
4.7.6. Методы расчета цепей синусоидального тока в символической форме.
Все методы расчета цепей постоянного тока (МКТ, МР и др.) применимы для цепей синусоидального тока в символической форме.
Метод узловых потенциалов, например:
4.7.7. Мощности в символической форме.
,
; ;