31. Необходимый признак сходимости числового ряда. Гармонический ряд
Сумма вида
называется
гармоническим числовым рядом.
Сумма вида
,
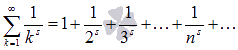где s – некоторое действительное
число, называется обобщенно
гармоническим числовым рядом.
ГАРМОНИЧЕСКИЙ РЯД
ЯВЛЯЕТСЯ
РАСХОДЯЩИМСЯ.
Докажем расходимость гармонического ряда.
Предположим, что ряд сходится.
Тогда существует конечный предел его
частичных сумм. В этом случае можно
записать
и
,
что приводит нас к равенству
.
С другой стороны,
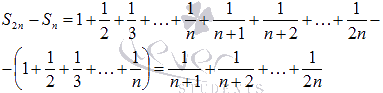
Не вызывают сомнения следующие
неравенства
.
Таким образом,
.
Полученное неравенство
указывает
нам на то, что равенство
не
может быть достигнуто, что противоречит
нашему предположению о сходимости
гармонического ряда.
Вывод: гармонический ряд расходится.
ОБОБЩЕННО ГАРМОНИЧЕСКИЙ
РЯД
СХОДИТСЯ
ПРИ s > 1 И РАСХОДИТСЯ ПРИ
.
Доказательство.
Для s = 1 получим гармонический ряд , а выше мы установили его расходимость.
При s < 1 справедливо
неравенство
для
всех натуральных k. В силу расходимости
гармонического ряда
можно
утверждать, что последовательность его
частичных сумм неограниченна (так как
не существует конечного предела). Тогда
последовательность частичных сумм
числового ряда
тем
более неограниченна (каждый член этого
ряда больше соответствующего члена
гармонического ряда), следовательно,
обобщенно гармонический ряд расходится
при s < 1.
Осталось доказать сходимость ряда при s > 1.
Запишем разность
:
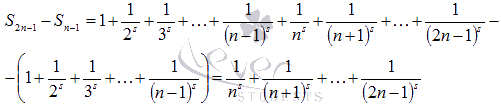
Очевидно, что
,
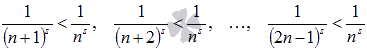тогда
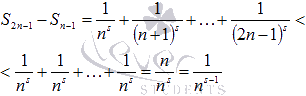
Распишем полученное неравенство
для n = 2, 4, 8, 16, …
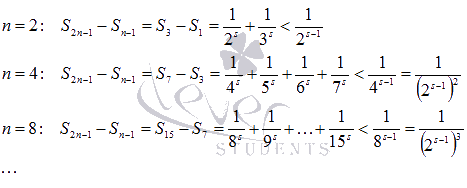
Используя эти результаты, с
исходным числовым рядом можно провести
следующие действия:
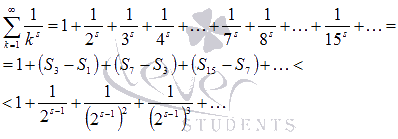
Выражение
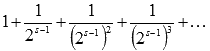представляет
собой сумму геометрической прогрессии,
знаменатель которой равен
.
Так как мы рассматриваем случай при s
> 1, то
.
Поэтому
.
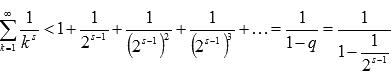Таким образом, последовательность
частичных сумм обобщенно гармонического
ряда при s > 1 является возрастающей
и в тоже время ограниченной сверху
значением
,
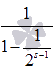следовательно, она имеет предел, что
указывает на сходимость ряда
.
Доказательство завершено.
32. Признаки сравнения для рядов с положительными членами. Табличные ряды
Пусть заданы два ряда с положительными членами: и .
Если, начиная с некоторого натурального числа N для всех n > N между соответствующими членами двух рядов устанавливается неравенство un ≥ vn, и ряд расходится, то и ряд также расходится.
Если, начиная с некоторого натурального числа N для всех n > N между соответствующими членами двух рядов устанавливается неравенство un ≤ vn , и ряд сходится, то и ряд также сходится.
Если существует конечный предел , отличный от нуля, то оба ряда и одновременно сходятся и одновременно расходятся. Такие ряды называются эквивалентными.
Рассмотрим два ряда, используемых при сравнении рядов.
Обобщенный гармонический ряд: . При α > 1 ряд сходится, при α ≤ 1 ряд расходится.
Ряд геометрической прогрессии: . При q < 1 ряд сходится, при q ≥ 1 ряд расходится.
33. Признак Даламбера
Если в ряде с положительными членами отношение (n +1)-го члена к n-му при имеет предел l , т.е. , то при l > 1 ряд расходится, при l < 1 ряд сходится, при l = 1 ряд может как сходиться, так и расходиться.
34. Радикальный признак Коши
Радикальный признак Коши
рассмотрим ряд
с
положительными членами. Согласно
признаку Коши:
Если
,
то ряд
сходится;
Если
,
то ряд
расходится;
Если
,
то вопрос о сходимости ряда
,
также как для признака Даламбера,
остается открытым.
35. Интегральный признак Коши
Пусть f (x) является непрерывной, положительной и монотонно убывающей функцией на промежутке [1, +∞). Тогда ряд
сходится, если сходится несобственный
интеграл
,
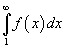и расходится, если
.
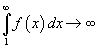36. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимость
Ряд вида , где un > 0 называется знакочередующемся. Если сходится ряд , то говорят, что знакочередующийся ряд сходится абсолютно.
Если знакочередующийся ряд не сходится абсолютно, то вопрос о его сходимости решает признак Лейбница: если то знакочередующийся ряд сходится, причем сумма S ряда будет положительной и меньше u1, т.е. 0 < S < u1.
Если знакочередующийся ряд сходится, но не сходится абсолютно, то говорят, что ряд сходится условно.