Тема: Елементи теорії визначників.

Мета: : формувати в студентів навики правильного мислення, вміння

міркувати, зіставляти і протиставляти факти, знаходити в них спільне і

характерне, робити правильні умовиводи. Виховувати в студентів

свідоме ставлення до навчання, розвивати пізнавальну активність і

культуру розумової праці.

План заняття.

1. Визначники ІІ порядку. Властивості визначників.

2. Визначники ІІІ порядку. Правило Саррюса.

3. Визначники n- ого порядку. Теорема Лапласа.

Означення 1. Визначником ІІ-го порядку називається число

(1)

Властивості визначників.

1. Якщо всі елементи деякого рядка(стовпця) визначника дорівнюють нулю, то визначник дорівнює нулю.

2. Від переставляння двох довільних рядків(стовпців) визначник змінює знак.

3. Якщо визначник містить два однакових рядки(стовпці), то він дорівнює нулю.

4. Якщо всі елементи деякого рядка(стовпця) визначника помножити на одне й те ж число, то весь визначник помножиться на це число.

5. Якщо всі елементи одного рядка(стовпця) визначника пропорційні відповідним елементам іншого рядка(стовпця), то визначник дорівнює нулю.

6. Якщо всі елементи і-того рядка(стовпця) визначника представлені у вигляді суми к доданків, то і весь визначник представляється у вигляді суми к визначників, у яких всі рядки(стовпці) крім і-того такі ж, як і в початкового визначника, а і-ий рядок(стовпець) у першому визначнику складається з перших доданків, у другому – з других і т.д.

7. Якщо до одного рядка(стовпця) визначника додати один або більше інших рядків (стовпців), помножених на будь-які числа, то значення визначника не зміниться.

8. Якщо хоча б один рядок(стовпець) визначника лінійно виражається через інші його рядки(стовпці), то він дорівнює нулю.

Означення 2. Визначником ІІІ-го порядку називається число

(2)

Тобто визначник третього порядку являє собою суму шести доданків, які являють собою добутки по три елементи. Щоб запам’ятати, які з них беруть із знаком “плюс”, а які із знаком “мінус”, користуються правилом Саррюса (правилом трикутника)

+ –

Означення 3. Мінором М_іj якого-небудь елемента a_ij визначника називається визначник нижчого порядку, одержаний із даного шляхом викреслювання і-го рядку та j-го стовпця, на перетині яких знаходиться елемент.

Означення 4. Алгебраїчним доповненням елемента a_ij визначника називається його мінор, взятий із знаком (-1)^і+j, тобто А_ij=(-1)^i+jM_ij.

Теорема Лапласа. Визначник n-го порядку дорівнює сумі добутків елементів якого-небудь рядка (стовпця) на їх алгебраїчне доповнення, тобто

(3)

Тема : Елементи теорії матриць

Мета : ознайомити студентів з поняттям матриці, властивостями матриць.

Формувати навички студентів виконання дій над матрицями,

обчислення оберненої матриці. Виховувати в студентів культуру

мислення та письма, акуратність, увагу.

План заняття.

1. Означення матриці.

2. Дії над матрицями.

3. Обернена матриця. Знаходження оберненої матриці.

Означення 1. Матрицею називається прямокутна таблиця, складена з елементів деякої множини, виду

(1)

Дії над матрицями.

1. Сумою двох матриць називається така матриця, кожен елемент якої дорівнює сумі відповідних елементів доданків.

2. Добутком матриці А на число λ називається така матриця, кожен елемент якої дорівнює відповідному елементу матриці А помноженому на число λ.

3. Транспонуванням називається перетворення матриці при якому рядки і стовпці міняються місцями.

4. Добутком матриці А на матрицю В називається така матриця С, кожен елемент якої, що стоїть на перетині і-го рядка і j-го стовпця, дорівнює сумі добутків елементів і-го рядка матриці А на елементи j-го стовпця матриці В.

Зауваження 1. Добуток А·В можливий лише тоді, коли кількість стовпців матриці А дорівнює кількості рядків матриці В.

Зауваження 2. Добуток АВ ВА.

Означення 2. Матриця виду Е= (2)

називається одиничною.

Означення 3. Якщо для матриці А існує така матриця В, для якої А·В=Е, то матриця В називається оберненою до матриці і позначається А^-1. Отже, А·А^-1=Е.

Означення 4. Матриця називається неособливою, якщо її визначник відмінний нулю.Для всякої неособливої матриці існує обернена.

Обернену матрицю знаходимо за такою схемою:

1. Знаходимо визначник матриці ( якщо визначник матриці дорівнює нулю то оберненої матриці не існує).

2. Знаходимо алгебраїчні доповнення до елементів матриці.

3. Утворюємо матрицю , елементами якої є знайдені алгебраїчні доповнення.

4. Транспонуємо матрицю (одержана матриця називається приєднаною).

5. Поділимо приєднану матрицю на визначник матриці.

Тема : Загальна теорія систем лінійних алгебраїчних рівнянь.

Мета: Узагальнення та систематизація знань студентів про системи

лінійних алгебраїчних рівнянь та методи їх розв’язування. Формувати в

студентів навики правильного мислення, вміння міркувати, зіставляти і

протиставляти факти, знаходити в них спільне і характерне, робити

правильні умовиводи. Виховувати в студентів свідоме ставлення до

навчання, розвивати пізнавальну активність і культуру розумової праці.

План заняття.

1. Системи лінійних алгебраїчних рівнянь.

2. Умови сумісності систем лінійних алгебраїчних рівнянь.

3. Методи розв’язування систем рівнянь:

• метод Крамера;

• метод оберненої матриці;

• метод Гаусса;

• метод Жордана – Гаусса.

Означення. Системою n лінійних рівнянь з n невідомими називається система виду:

а₁₁х₁+ а₁₂х₂+…+ а_1nх_n=b₁

а₂₁х₁+ а₂₂х₂+…+ а_2nх_n=b₂

………………………………

а_n1х₁+ а_n2х₂+…+ а_nnх_n=b_n

Якщо b₁=b₂=…b_n=0, то система називається однорідною, в противному випадку неоднорідною. b₁,b₂,…,b_n – називається вільними членами, коефіцієнти, які стоять біля невідомих х₁,х₂,…,х_n утворюють матрицю, визначник якої називається визначником системи і позначається Δ.

Система рівнянь називається сумісною, якщо вона має розв’язки.

Система рівнянь називається визначеною, якщо вона має лише один розв’язок.

Введемо наступні позначення:

тоді дана система запишеться у вигляді АХ=В, звідки розв’язок системи обчислюється за формулою Х=А^-1·В.

Отже, розв’язування системи зводиться до відшукання оберненої матриці. Цей метод називається методом оберненої матриці.

Крім матричного способу існує ще й метод Крамера.

Нехай Δ 0. Позначимо через Δ_і визначник, який одержимо із А шляхом заміни і-го стовпця стовпцем вільних членів, тобто

,…,

тоді …

Якщо Δ=0, і принаймі один з визначників Δ_і 0 то система рівнянь не сумісна.

Якщо Δ=0, і всі визначники Δ_і =0 то система рівнянь має безліч розв'язків.

Метод Гаусса. Даний метод полягає в послідовному виключенні х₁ з усіх рівнянь крім першого, х₂ – з усіх рівнянь, починаючи з третього, і т.д. Тобто зведенні системи рівнянь до трикутного вигляду. Отримана система матиме єдиний розв’язок та розв’язується, починаючи з останнього рівняння.

Тема : Вектори. Лінійна залежність та лінійна незалежність векторів. Розклад вектора за базисом. Скалярний , векторний і мішаний добутки векторів.

Мета: Узагальнення та систематизація знань студентів про вектор.

Формувати в студентів навики правильного мислення, вміння міркувати,

зіставляти і протиставляти факти, знаходити в них спільне і характерне,

робити правильні умовиводи. Виховувати в студентів свідоме ставлення

до навчання, розвивати пізнавальну активність і культуру розумової

праці.

План заняття.

1. Вектор. Дії над векторами.

2. Векторний добуток та його властивості.

3. Мішаний добуток та його властивості.

Поняття про векторні та скалярні величини

Величини, які зустрічаються в механіці, фізиці та інших прикладних науках, можуть бути розділені на дві категорії. З одного боку, існують такі фізичні або механічні величини, які визначаються тільки числом: маса, густина, температура, об’єм, потенціал. Ці величини називаються скалярними величинами, або просто скалярами. З другого боку, є такі величини, які для свого визначення потребують не тільки числового значення, але й напрямку, наприклад: сила, швидкість, прискорення, напруженість. Такі величини називають векторними величинами, або векторами. Скалярна величина може бути задана числом, яке виражає відношення цієї величини до відповідної одиниці виміру. Геометричною моделлю векторної величини є прямолінійний відрізок з вибраним на ньому напрямком.

Вектор як направлений відрізок записується в виді двох великих латинських букв із стрілкою згори, причому перша буква означає початок вектора, а друга - його кінець, наприклад, - вектор, в якого точка є початком, а - кінцем. Іноді стрілку над буквами не ставлять, а виділяють ці букви жирним шрифтом. Під довжиною вектора будем розуміти віддаль між початком і кінцем вектора. Довжину, або, як часто говорять, модуль вектора будемо позначати символом . Очевидно, вектори і мають однакову довжину (тобто = ) і протилежний напрямок.

Вектор повністю визначається своїми початком і кінцем. Він може бути, звичайно, заданий також початком, або, іншими словами, точкою прикладання, довжиною і напрямком. Однак в багатьох випадках точка прикладання (початок) вектора не має значення - мають значення лише довжина вектора та його напрямок. Такі вектори називаються вільними векторами. Вільні вектори позначають одною малою латинською буквою, наприклад, . Оскільки точка прикладання вільного вектора не має значення, то такий вектор можна переносити в будь-яку точку простору, зберігаючи при цьому його довжину і напрямок.

Вектори рівні, якщо при їх паралельному переносі і суміщенні початків будуть суміщені і кінці.

Вектор , початок і кінець якого співпадають, називають нульовим. Його модуль рівний нулю. Нульовий вектор не має певного напрямку. Якщо вектори і рівні по модулю, паралельні, але направлені в протилежні сторони; такі вектори називаються взаємно або просто протилежними. Вектор, протилежний вектору , позначають через .

Колінеарними називають вектори, які лежать на паралельних прямих. Інакше кажучи, вектори колінеарні, якщо при паралельному їх переносі і суміщенні початків вони лежать на одній прямій.

Компланарними називають вектори, які лежать в паралельних площинах. Інакше кажучи, вектори компланарні, якщо при паралельному їх переносі і суміщенні початків вони лежать в одній площині. Очевидно, що два вектори завжди компланарні.

Лінійні операції над векторами

Вводячи різні операції над векторами, збережемо прийняті в алгебрі чисел терміни "додавання" і "множення". Однак слід мати на увазі, що оскільки поняття "вектор" і "число" суттєво різні, то зміст операцій, що вводяться, може не співпадати з відповідними операціями алгебри чисел. Тому потрібно дослідити основні правила цих, по суті справи, нових операцій.

ОЗНАЧЕННЯ. Сумою двох векторів і називається третій вектор , початком якого є початок першого вектора, кінцем - кінець другого, причому початок другого вектора суміщений з кінцем першого.

Рис. 1

1. Додавання векторів підлягає переставному закону

для любих векторів і .

Це правило справедливе і в випадку колінеарності векторів і , а також у випадку нульових і .

Зокрема, .

2. Додавання векторів підлягає сполучному закону

для любих векторів , , і тому суму трьох векторів можна записати просто в виді .

Операція додавання векторів може бути поширена на будь-яку кількість доданків.

Може трапитись, що кінець останнього вектора співпадає з початком першого і, отже, у замикаючого вектора кінець співпадає з початком. В цьому випадку сума векторів є нульовий вектор.

Різницю векторів і називають такий вектор , що .

Відмітимо, що в паралелограмі, побудованому на даних векторах і , їх сумою є діагональ, що виходить із спільної точки їх прикладання, а різницею є відповідно направлена друга діагональ паралелограма.

Справедливе таке правило віднімання:

.

Означення. Добутком вектора на скаляр називається вектор

,що має довжину , а його напрямок

1) співпадає з напрямком вектора , якщо ;

2) протилежний , якщо ;

3) довільний, якщо .

Скалярним добутком двох векторів називається добуток довжин цих векторів на косинус кута між ними. (При цьому мається на увазі кут між векторами, початки яких перенесені в одну і ту ж точку).

Скалярний добуток векторів і позначають , - кут між векторами і .

Очевидно, що скалярний добуток векторів і буде рівний нулю, якщо хоч би один із векторів і є нульовим вектором або якщо вектори перпендикулярні (ортогональні). Якщо хоч би один із векторів і нульовий, то слід вважати довільним. Навпаки, якщо , то хоч би один із векторів і нульовий або ці вектори перпендикулярні.

Оскільки (читається: проекція вектора на напрямок вектора ), (проекція вектора на напрямок вектора ), то можна записати:

. Таким чином, скалярний добуток двох векторів рівний довжині одного вектора, помноженій на проекцію другого на напрямок першого.

Розглянемо деякі властивості скалярного добутку.

1. Скалярний добуток підлягає переставному закону, тобто для любих векторів і .

2. Скалярний добуток підлягає сполучному закону відносно скалярного множника, тобто для будь-яких векторів і і будь-якого числа .

3. Скалярний добуток підлягає розподільному закону, тобто для будь-яких векторів , , .

 4. Скалярний квадрат вектора рівний квадрату його модуля. Домножимо скалярно вектор на вектор :

 Скалярний добуток називається скалярним квадратом вектора і позначається . На основі тільки що записаної властивості отримуємо: , звідси, зокрема, .

5. якщо , навпаки, , якщо і .

Скалярний добуток векторів в координатній формі

Якщо вектори і задані своїми координатами: , то їх скалярний добуток визначається формулою:

.

Кут між векторами і визначається рівністю:

.  

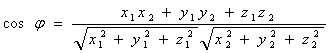Дійсно, за означенням скалярного добутку

.

Звідки .

 

Якщо вектори і перпендикулярні, то і, отже, x₁x₂+y₁y₂+z₁z₂=0. І навпаки, якщо x₁x₂+y₁y₂+z₁z₂=0, то вектори і перпендикулярні.

Векторним добутком вектора на вектор називається такий третій вектор , довжина якого чисельно рівна площі паралелограма, побудованого на векторах і , а напрямок перпендикулярний до площини паралелограма, побудованого на даних векторах, причому вектор направлений так, що із кінця вектора видно, що коли дивитись з кінця вектора , то поворот від до на найменший кут відбуваєть­ся проти годинникової стрілки (див.рис).

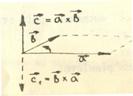
Векторний добуток заданих векторів і позначається .

Оскільки площа паралелограма, побудованого на векторах і рівна добутку довжин цих векторів і синуса кута між ними, то .

  Розглянемо основні властивості векторного добутку векторів і .

1. Відмітимо перш за все, що для будь-яких векторів і .

Отже, векторний добуток не підлягає переставному закону.

2. Векторний добуток має властивість

.

3. Векторний добуток підлягає також розподільному закону, тобто

4. Векторний добуток векторів в координатній формі

Використовуючи дані властивості векторного добутку, можна отримати формули для обчислення векторного добутку векторів

, .

Після перемноження правих частин, заміни векторних добутків ортів їх значеннями і зведення подібних членів отримаємо

Для скороченого запису векторного добутку можна використовувати визначник третього порядку. Дійсно, праву частину останньої рівності можна трактувати як розклад визначника третього порядку

по елементах першої стрічки. Тоді .

Мішаний добуток векторів. Нехай дані три вектори , , . Знайдемо векторний добуток і домножимо його скалярно на третій вектор : . Таке множення векторів називається векторно – скалярним, або мішаним добутком трьох векторів. В результаті цього множення отримується число. Покажем, що коли вектори , , некомпланарні, то це число рівне об’єму паралелепіпеда, побудованого на векторах , , , взятому із знаком плюс, якщо вектори , , утворюють праву трійку векторів (в випадку правої системи координат це означає, що, якщо дивитись із кінця вектора , то найкоротший поворот від вектора до вектора відбувається проти годинникової стрілки, при цьому припускається, що вектори , , мають спільний початок). Знак мінус ставиться в протилежному випадку.

Абсолютна величина мішаного добутку рівна об’єму V паралелепіпеда, побудованого на векторах , і : .

Тепер знайдемо мішаний добуток векторів в координатній формі. Нехай задані три вектори в координатній формі:

Запишемо спочатку векторний добуток векторів і в координатній формі:

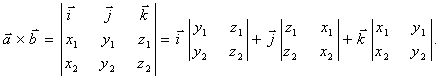
 Врахуємо, що скалярний добуток векторів рівний сумі добутків відповідних координат цих векторів.

,

 

.

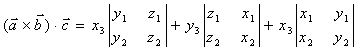Формула дає вираз мішаного добутку в координатній формі. Із неї видно, що мішаний добуток векторів , і рівний нулю тоді і тільки тоді, коли вектори , , лежать в одній площині або в паралельних площинах. Такі вектори називають компланарними. Таким чином, рівність є умовою компланарності векторів , , .

При круговій перестановці векторів мішаний добуток не змінюється, а при будь-якій іншій перестановці змінюється знак:

(Круговою перестановкою векторів , , називається така

перестановка, коли стає на місце , на місце , на місце ).

Тема: Лінії на площині .

Мета: вивчення основних формул рівняння ліній на площині та в просторі.

Формування в студентів вмінь використовувати вивчені формули на

практиці. Виховувати в студентів культуру мислення та письма,

акуратність, увагу.

План заняття.

1. Рівняння лінії на площині.

2. Пряма на площині:

• загальне рівняння прямої;

• канонічне рівняння прямої;

• параметричне рівняння прямої;

• рівняння з кутовим коефіцієнтом.

3. Відстань від точки до прямої.

Будь-яка пряма на площині в прямокутній системі координат визначається рівнянням першого ступеня відносно координат її довільної точки, і, навпаки, кожне рівняння першого степеня відносно х і у визначає деяку пряму на площині.

Основні відомості з теорії

1. Рівняння прямої з кутовим коефіцієнтом

, (1)

параметр к – називається кутовим коефіцієнтом прямої, причому к=tgα, де α – кут нахилу прямої до додатнього напрямку осі Ох, параметр b визначає довжину відрізка, який відтинає пряма на осі Оу.

2. Загальне рівняння прямої

Ах+Ву+С=0, (2)

де А і В – коефіцієнти, які одночасно не рівні нулю.

3. Рівняння прямої у відрізках на осях:

, (3)

де а, b – довжини відрізків, які відтинає пряма на осях координат.

4. Рівняння в’язки прямих, що проходить через точку М(х₀;у₀):

у-у₀=к(х-х₀­). (4)

5. Рівняння прямої, що проходить через дві задані точки А(х₁,y₁), B(x₂,y₂):

(5)

6. Кут φ відрахований проти годинникової стрілки від прямої у=к₁х+b₁, до прямої у=к₂х+b₂ визначається за формулою

(6)

Для прямих, заданих рівняннями А₁х+В₁у+С₁=0, А₂х+В₂у+С₂=0 формула (6) прийме вигляд

.

Умова паралельності прямих має вигляд: к₁=к₂, або .

Умова перпендикулярності двох прямих має вигляд: , або А₁А₂+В₁В₂=0.

7. Нормальне рівняння прямої

xcosβ+ysinβ-p=0, (7)

де р – довжина перпендикуляра (нормалі), опущеного з початку координат на пряму;

β – кут нахилу цього перпендикуляра до осі Ох.

8. Відстань від точки М(х₀;у₀) до прямої заданої загальним рівнянням (2) обчислюється за формулою

, (8)

9. Рівняння в’язки прямих, що проходять через точку перетину двох прямих:

.

Лінії в просторі

Будь-яка площина в просторі може бути задана рівнянням першого степеня відносно біжучих координат. Навпаки, будь-яке рівняння першого степеня відносно біжучих координат (х;у) визначає площину.

Основні відомості з теорії

1. Рівняння площини, яка проходить через точку M₁(x₁,y₁,z₁) перпендикулярно до нормального вектора (А,В,С)

A(x-x₁)+B(y-y₁)+C(z-z₁)=0. (1)

2. Загальне рівняння площини

Ах+Ву+Сz+D=0. (2)

3. Рівняння площини у відрізках на осях координат

(3)

де а,b,c – величини відрізків, що відтинаються площиною на координатних осях Ох, Оу, Оz відповідно.

4. Нормальне рівняння площини

(4)

– кути між осями координат Ох, Оу, Оz і перпендикуляром, опущеним з початку координат на площину;

р – довжина цього перпендикуляра.

5. Для зведення рівняння (4) до нормального виду потрібно його помножити на нормуючий множник

вибравши знак, протилежний знаку вільного члена р.

6. Кут між двома площинами

(5)

де , – нормальні вектори до площин.

7. Умова перпендикулярності

АА₁+ВВ₁+СС₁=0.

Умова паралельності двох площин має вид:

8. Відстань від точки M₀(x₀,y₀,z₀) до площини (2)

. (6)

9. Рівняння в’язки площин, що проходять через лінію перетину двох площин

Ах+Ву+Сz+D+λ(A₁x+B₁y+C₁z+D₁)=0, (7)

де λ – довільне дійсне число.

Тема: Площина і пряма в просторі.

1. Рівняння площини у просторі.

2. Рівняння прямої у просторі.

Будь-яке рівняння першого степеня з трьома змінними визначає площину. І навпаки, будь-яка площина визначається рівнянням першого степеня відносно змінних координат, які задають довільну точку площини.

1. Загальне рівняння площини

Загальне рівняння площини має вигляд:

Де числа координати нормального вектора.

Особливі випадки рівняння

а) Якщо в рівнянні вільний член , тоді одержуємо рівняння

Площини, що проходить через початок координат.

б) Нехай в рівнянні один із коефіцієнтів або С дорівнює нулю. Тоді одержимо рівняння площини, які паралельні відповідним координатним осям.

Рівняння площини, що паралельні осі .

Рівняння площини, що паралельні осі :

Рівняння площини, що паралельна осі :

Необхідно запам’ятати, що якщо площина паралельна якій-небудь координатній осі, то в її рівняння відсутній член, який містить координату, однойменну з цією віссю.

в) Якщо в цих рівняннях вільний член , то одержимо рівняння площин, які проходять через відповідні осі координат.

Рівняння площини, що проходить через вісь :

.

Рівняння площини, що проходить через вісь :

.

Рівняння площини, що проходить через вісь :

.

г) Нехай в рівнянні два коефіцієнта дорівнюють нулю, тобто: , або , або . Тоді одержуємо рівняння площини, які паралельні відповідним координатним площинам:

Рівняння площини, що паралельна координатній площині :

, або .

Рівняння площини, що паралельна координатній площині :

, або

Рівняння площини, що паралельна координатній площині :

, або .

д) нехай в рівнянні три коефіцієнти , або і , або і дорівнює нулю. Тоді одержуємо рівняння координатних площин.

Рівняння координатної площини :

, або .

Рівняння координатної площини :

, або .

Рівняння координатної площини :

, або .

2. Рівняння площини в відрізках.

Рівняння площини в відрізках має вигляд:

Де і - величини відрізків, які відтинає площина на осях координат.

3. Рівняння площини, що проходить через задану точку

Рівняння площини, що проходить через задану точку має вигляд:

,

Де - координати нормального вектора площини

4. Рівняння площини, що проходить через три задані точки

Рівняння площини, що проходить через три задані точки , і , які не лежать на одній прямій має вигляд:

.

Кут між двома площинами, які задані рівняннями:

Визначається за формулою:

Умова паралельності двох площин має вигляд:

Умова перпендикулярності двох площин має вигляд:

.

Відстань від точки до площини визначається за формулою:

.

2. У просторі, як і на площині, пряма може задаватись різними способами.

1) Рівняння прямої, заданої точкою і напрямним вектором (канонічне рівняння прямої).

Напрямний вектор прямої , точка М₀(x_0,y_0,z₀) – належить прямій. Візьмемо довільну точку М (x,y,z) і розглянемо умову, коли точка М належить прямій. Для цього потрібно, щоб , тоді їх координати повинні бути пропорційні, тобто

2) Рівняння прямої заданої, двома точками.

Нехай точки М₁(x₁,y₁,z₁), М₂(x₂,y₂,z₂) належать прямій. Візьмемо довільну точку М (x,y,z) на прямій і утворимо вектори М₁М₂ і М₁М, тоді М₁М₂ || М₁М, а значить

.

3) Рівняння прямої, заданої двома площинами.

.

.

Тоді пряма розглядається, як перетин двох площин.

Отже, рівняння прямої

Напрямним вектором прямої, заданої, як перетин двох площин є вектор

4) Параметричні рівняння прямої.

Розглянемо канонічне рівняння прямої і введемо коефіцієнт пропорційності:

. Тоді

Взаємне розміщення двох прямих.

Нехай у деякій системі координат дано дві прямі канонічними рівняннями:

;

.

1) Прямі d₁ і d₂ будуть паралельними тоді і тільки тоді, коли їх напрямні вектори і є колінеарними. Тобто, координати векторів будуть пропорційними:

d₁ d₂

2) Дві прямі збігаються тоді і тільки тоді, коли дві прямі мають спільну точку і їх напрямні вектори колінеарні:

х₁=х₂, y₁=y₂, z₁=z₂

3) Дані непаралельні прямі будуть перетинатися тоді і тільки тоді, коли вектори компланарні, тобто їх мішаний добуток дорівнює нулю .

Одержана умова є умовою і того, що дві прямі лежать в одній площині.

4) Дві прямі будуть мимобіжними, якщо вони непаралельні і не перетинаються.

Кут між двома прямими.

Нехай у просторі дано дві непаралельні прямі d₁ i d₂.

Візьмемо довільну точку А простору і проведемо через цю точку дві прямі // d₁^¢ i d₂^¢

А

Тоді кутом між прямими i будуть називатися кут між прямими причому

.

Якщо дві прямі задано канонічними рівняннями, то визначення кута між двома прямими зводиться до визначення кута між двома напрямними векторами цих прямих.

А

А

Отже,

Дві прямі перпендикулярні, коли скалярний добуток напрямних векторів дорівнює нулю: тобто .

Задача 1. Знайти проекцію точки на площину

Розв’язок: а) Складено рівняння прямої, що проходить через точку перпендикулярно до площини Спочатку напишемо рівняння прямої, що проходить через точку :

На основі умови перпендикулярності прямої і площини числа пропорційні числам із рівняння площини. Через це, замінивши в останньому рівнянні числами одержуємо рівняння прямої в вигляді:

б)Щоб знайти проекцію точки на площину, необхідно знайти координати основи перпендикуляра, проведеного із точки на площину, тобто точку перетину прямої з площиною.

Рівняння прямої представляємо в параметричній формі. Одержимо: Одержані значення підставляємо в рівняння площини:

Значення параметра підставимо в рівняння

Маємо:

Отже, проекція точки на площину є точка .

Задача 2. Скласти рівняння площини, що проходить через точку і пряму

Розв’язок. В шуканій площині повинні знаходиться точка та пряма Виберемо в шуканій площині точку . Якщо пряма лежить у шуканій площині, то точка заданої прямої знаходиться в площині, а напрямний вектор паралельний шуканій площині. Розглянемо вектори , та . Ці вектори компланарні, а це означає. Що їх мішаний добуток дорівнює нулю:

Або

Розкриваємо визначник:

Ми отримали рівняння шуканої площини.

Тема: Математична обробка даних.

Метод найменших квадратів

У процесі вивчення різних питань природознавства, економіки і техніки, соціології, педагогіки доводиться на основі великої кількості дослідних даних виявляти суттєві фактори, які впливають на досліджуваний об’єкт, а також встановлювати форму зв’язку між різними зв’язаними одна з одною величинами (ознаками).

Нехай у результаті досліджень дістали таку таблицю деякої функціональної залежності:

Таблиця 1

x	x1	x2	…	xn
y	y1	y2	…	yn

Треба знайти аналітичний вигляд функції , яка добре відображала б цю таблицю дослідних даних. Функцію можна шукати у вигляді інтерполяційного поліному. Але інтерполяційні поліноми не завжди добре відображають характер поведінки таблично заданої функції. До того ж значення дістають у результаті експерименту, а вони, як правило, сумнівні. У цьому разі задача інтерполювання табличної функції втрачає сенс. Тому шукають таку функцію , значення якої при досить близькі до табличних значень . Формулу називають емпіричною, або рівнянням регресії на . Емпіричні формули мають велике практичне значення, вдало підібрана емпірична формула дає змогу не тільки апроксимувати сукупність експериментальних даних, «згладжуючи» значення величини , а й екстраполювати знайдену залежність на інші проміжки значень .

Процес побудови емпіричних формул складається з двох етапів: встановлення загального виду цієї формули і визначення найкращих її параметрів.

Щоб встановити вигляд емпіричної формули, на площині будують точки з координатами . Деякі з цих точок сполучають плавною кривою, яку проводять так, щоб вона проходила якомога ближче до всіх даних точок. Після цього візуально визначають, графік якої з відомих нам функцій найкраще підходить до побудованої кривої. Звичайно, намагаються підібрати найпростіші функції: лінійну, квадратичну, дробово-раціональну, степеневу, показникову, логарифмічну.

Встановивши вигляд емпіричної формули, треба знайти її параметри (коефіцієнти). Найточніші значення коефіцієнтів емпіричної формули визначають методом найменших квадратів. Цей метод запропонували відомі математики К. Гаусс і А. Лежандр.

Розглянемо суть методу найменших квадратів.

Нехай емпірична формула має вигляд

, (1)

де , , …, - невідомі коефіцієнти. Треба знайти такі значення коефіцієнтів , за яких крива (1) якомога ближче проходитиме до всіх точок , , …, , знайдених експериментально. Зрозуміло, що жодна з експериментальних точок не задовольняє точно рівняння (1). Відхилення від підстановки координат у рівняння (1) дорівнюватимуть величинам .

За методом найменших квадратів найкращі значення коефіцієнтів ті, для яких сума квадратів відхилень

(2)

дослідних даних від обчислених за емпіричною формулою (1) найменша. Звідси випливає, що величина (2), яка є функцією від коефіцієнтів , повинна мати мінімум. Необхідна умов мінімуму функції багатьох змінних ─ її частинні похідні мають дорівнювати нулю, тобто

, , …, .

Диференціюючи вираз (2) по невідомих параметрах , матимемо відносно них систему рівнянь:

Система (3) називається нормальною. Якщо вона має розв’язок, то він єдиний, і буде шуканим.

Якщо емпірична функція (1) лінійна відносно параметрів , то нормальна система (3) буде системою з лінійних рівнянь відносно шуканих параметрів.

Будуючи емпіричні формули, припускатимемо, що експериментальні дані додатні.

Якщо серед значень і є від’ємні, то завжди можна знайти такі додатні числа і , що і .

Тому розв’язування поставленої задачі завжди можна звести до побудови емпіричної формули для додатних значень .

Побудова лінійної емпіричної формули. Нехай між даними існує лінійна залежність. Шукатимемо емпіричну формулу у вигляді

, (4)

де коефіцієнти і невідомі.

Знайдемо значення і , за яких функція матиме мінімальне значення. Щоб знайти ці значення, прирівняємо до нуля частинні похідні функції

Звідси, врахувавши, що , маємо

(5)

Розв’язавши відносно і останню систему, знайдемо

, (6)

. (7)

Зазначимо, що, крім графічного, є ще й аналітичний критерій виявлення лінійної залежності між значеннями і .

Покладемо , , .

Якщо , то залежність між і лінійна, бо точки лежатимуть на одній прямій. Якщо , то між і існує майже лінійна залежність, оскільки точки лежатимуть близько до деякої прямої.

Побудова квадратичної емпіричної залежності. Нехай функціональна залежність між та - квадратична. Шукатимемо емпіричну формулу у вигляді

. (8)

Тоді формулу (2) запишемо наступним чином

Для знаходження коефіцієнтів , , , за яких функція мінімальна, обчислимо частинні похідні , , і прирівняємо їх до нуля. В результаті дістанемо систему рівнянь

Після рівносильних перетворень маємо систему

(9)

Розв’язок цієї системи і визначає єдину параболу, яка краще від усіх інших парабол (8) подає на розглядуваному проміжку задану таблично функціональну залежність.

Сформулюємо аналітичний критерій для квадратичної залежності. Для цього введемо поділені різниці першого і другого порядку

і , де .

Точки розміщені на параболі (8) тоді і тільки тоді, коли всі поділені різниці другого порядку зберігають сталі значення.

Якщо точки рівновіддалені, тобто , то для існування квадратичної залежності (8) необхідно і достатньо, щоб була сталою скінчена різниця другого порядку , причому .

Побудова емпіричних формул найпростіших нелінійних залежностей. Нехай у системі координат маємо нелінійну залежність , неперервну і монотонну на відрізку .

Введемо змінні , так, щоб у новій системі координат задана емпірична нелінійна залежність стала лінійною

. (10)

Тоді точки з координатами в площині лежатимуть на прямій лінії.

Покажемо, як від нелінійних залежностей

, 2) , 3) ,

, 5) , 6)

перейти до лінійних.

1) Розглянемо степеневу залежність , де , , .

Логарифмуючи її, знаходимо . Звідси, поклавши , , , , маємо .

2) Логарифмуючи показникову залежність , маємо . Поклавши , , , в системі координат дістанемо залежність (10).

Зазначимо, що замість показникової залежності часто шукають залежність . Остання перетвориться в лінійну, якщо позначити , , , .

3) Щоб перейти від логарифмічної залежності до лінійної , досить зробити підстановку , .

4) У гіперболічній залежності замінимо змінні , . Тоді гіперболічна залежність перетвориться в лінійну (10), в якій , .

5) Розглянемо дробово-лінійну функцію . Знайдемо обернену функцію . Тоді ввівши нові координати , , дістанемо лінійну залежність (10), де , .

6) Нехай маємо дробово-раціональну залежність . Оберненою до неї буде залежність . Ввівши нові змінні , , дістанемо лінійну залежність (10) з коефіцієнтами , .

Отже, для побудови будь-якої з емпіричних формул 1)-6) треба:

а) за вихідною таблицею даних побудувати нову таблицю , використавши відповідні формули переходу до нових координат;

б) за новою таблицею даних знайти методом найменших квадратів коефіцієнти і лінійної функції (10);

в) за відповідними формулами знайти коефіцієнти і даної нелінійної залежності.

Вибрати емпіричну формулу для нелінійних залежностей графічним методом часто буває важко. Тоді вдаються до перевірки аналітичних критеріїв існування певної залежності. Для цього зводять її до лінійної і перевіряють виконання критерію лінійної залежності між перетвореними вихідними даними . Але є й власні аналітичні критерії наявності кожної з розглянутих вище нелінійних залежностей. Найпростіші необхідні умови їх наявності подано в табл. 2.

Таблиця 2

№ пор.	Емпірична формула			Спосіб вирівнювання
1
2				, де , , ,
3				, де , ,
4				, де
5				, де
6				, де
7				, де ,

Умови перевіряють у такий спосіб. На заданому відрізку зміни незалежної змінної вибирають дві точки, досить надійні і розміщені якомога далі одна від одної. Нехай, наприклад, це будуть точки , . Потім, залежно від типу емпіричної формули, що перевіряється, обчислюють значення , яке є або середнім арифметичним, або середнім геометричним, або середнім гармонічним значень , . Маючи значення і аналогічно обчислюють і відповідне значення . Далі, користуючись даною таблицею значень , для значення знаходять відповідне йому значення . Якщо немає в таблиці, то знаходять наближено з побудованого графіка даної залежності або за допомогою лінійної інтерполяції , де і ─ проміжні значення, між якими лежить . Обчисливши , знаходять величину . Якщо ця величина велика, то відповідна емпірична формула не придатна для апроксимації заданих табличних даних. З кількох придатних емпіричних формул перевагу надають тій, для якої відхилення якомога менше.

Тема : Функції та їх основні властивості.

Мета: Повторити набуті знання з теми «Функції».

Формування вмінь студентів в обчисленні визначних границь.

Виховання в студентів активного ставлення до навчання, розвиток

пізнавальної діяльності та культури розумової праці.

План заняття

1. Повторення вивченого на І курсі:

- поняття функції, основні властивості функцій;

Поняття функції є одним із центральних понять математичного аналізу, яке виражає ідею взаємного зв’язку змінних величин.

Означення функції. Якщо кожному значенню змінної х за певним правилом чи законом ставиться у відповідність єдине значення у є Y, то змінна у називається функцією від змінної х.

Незалежна змінна х називається аргументом функції.

Основні елементарні функції:

1. Степенева функція: ,

2. Показникова функція: , а>0, a 1

3. Логарифмічна функція: y=log_ax, а>0, a 1

4. Тригонометричні функції: y=sinx; y=cosx; y=tgx; y=ctgx

5. Обернені тригонометричні функції: y=arcsinx; y=arccosx; y=arctgx; y=arcctgx

 Область визначення функції – множина тих значень х при яких функція має зміст, тобто для кожного дійсного числа х₀ із області існування можна одержати дійсне число f(х₀).

    Область значень функції (множина значень) - усі значення, яких набуває функція.     Функція є парною - якщо для будь-якого х з області визначення функції виконується рівність f(x)=f(-x)     Функція є непарною - якщо для будь-якого х з області визначення функції виконується рівність f(-x)=-f(x)     Зростаюча функція - якщо для будь-яких х₁ і х₂, таких, що х₁< х₂, виконується нерівність f(х₁)<f(х₂)     Спадна функція - якщо для будь-яких х₁ і х₂, таких, що х₁< х₂, виконується нерівність f(х₁)>f(х₂)

Тема :Границя функції .Неперервність функції.

Мета Введення поняття границі функції та її основних властивостей. Формування вмінь студентів в обчисленні визначних границь.

Виховання в студентів активного ставлення до навчання, розвиток

пізнавальної діяльності та культури розумової праці.

План заняття

1. Означення границі;

- основні властивості границі.

2. Перша та друга визначні границі.

3. Обчислення невизначеностей типу .

4. Неперервність функції.

Границя функції. Число А називається границею функції f(x), при , , якщо для будь-якого наперед заданого додатного як завгодно малого числа ε існує таке додатне число δ, залежне від ε, що із нерівності , випливає нерівність і записується у вигляді .

Властивості границь.

1. Границя сталої,дорівнює самій сталій.

2. Сталий множник можна винести за знак границі

3. Границя суми(різниці) двох функцій дорівнює сумі(різниці) двох функцій

4. Границя добутку двох функцій дорівнює добутку границь

5. Границя частки рівна частці границь

Основні типи границь

Границі виду називаються невизначеностями.

До першого типу віднесемо границі виду , де P(x),G(x) – многочлени (а – скінченне число). Щоб розкрити цю невизначеність треба знаменник і чисельник дробу поділити на (х-а).

До другого типу віднесемо границі виду , де P(x),G(x) – многочлени або інші функції, що мають границі ∞. Щоб розкрити цю невизначеність треба знаменник і чисельник дробу поділити на , де n- найвищий степінь х, який входить в дріб.

До третього типу віднесемо границі з невизначеністю виду , де P(x),G(x) – ірраціональні функції. Щоб розкрити цю невизначеність треба знаменник і чисельник дробу домножити на спряжені вирази.

До четвертого типу віднесемо границі, в які входять тригонометричні чи обернені тригонометричні функції та містять невизначеність виду .Для знаходження таких границь необхідно використати першу визначну границю:

.

До п’ятого відноситься невизначеність виду .

Друга визначна границя має вигляд

, е- основа натурального логарифма, е=2,71…

Тема: Похідна функції.

1. Похідна, її фізичний та геометричний зміст.

2. Формули диференціювання.

Поняття похідної – фундаментальне поняття математичного аналізу, за допомогою якого досліджують процеси і явища в природничих, соціальних і економічних науках. Вивчення різних процесів (механічного руху, хімічних реакцій, розширення рідини при нагрівання, значення електричного струму та ін.) проводять до необхідності обчислення швидкості зміни різних величин, тобто до поняття похідної.

Нехай задано функцію на деякому проміжку. Візьмемо довільну внутрішню точку даного проміжку, надамо значенню довільного приросту (число може бути як додатним, так і від’ємним), але такого, щоб точка належала даному проміжку, тоді

1. Обчислимо в точці приріст функції:

;

2. Складемо відношення: .

3. Знайдемо границю цього відношення при умові, що , тобто:

.

Якщо дана границя існує, то її називають похідною функції в точці і позначають або (читається еф штрих від або штрих).

Похідною функції в точці називається границя відношення приросту функції до приросту аргументу при умові, що приріст аргументу прямує до нуля, а границя існує, тобто

.

Приклад 1. Знайдіть похідну функції в точці .

Розв’язання

Знайдемо приріст функції:

Знайдемо відношення приросту функції до приросту аргументу:

.

Знайдемо похідну даної функції в точці :

.

Якщо матеріальна точка рухається прямолінійно і її координата змінюється по закону , то швидкість її руху в момент часу дорівнює похідній :

Значення похідної функції в точці дорівнює кутовому коефіцієнту дотичної до графіка функції в точці з абсцисою :

Розглянемо функцію .

У точці проведено дотичну до кривої . Складемо рівняння дотичної АМ, знаючи координати точки дотику і рівняння кривої. Дотична – це пряма. Рівняння будь-якої прямої має вигляд: . Оскільки , тому рівняння дотичної має такий вигляд:

(1)

Знайдемо , виходячи з того, що дотична проходить через точку і тому її координати задовольняють рівнянню дотичної:

, звідси .

Тепер підставимо значення в рівняння (1) дотичної і одержимо:

Отже, рівняння дотичної до кривої в точці має вигляд:

. (2)

Приклад 1. Складіть рівняння дотичної до графіка функції в точці .

Розв’язання

1. - рівняння шуканої дотичної.

2. .

3.

Підставляємо значення у рівняння дотичної:

, або або

Формули диференціювання:

1. Якщо функція і диференційовані в точці , то їхня сума диференційована в цій точці і

.

або коротко говорять: похідна суми дорівнює сумі похідних.

Наслідки

а) Похідна різниці дорівнює різниці похідних.

б) Похідна суми декількох функцій дорівнює сумі похідних цих функцій, тобто .

Приклад. Знайдіть похідні функцій

а)

б)

в)

Розв’язання

а)

б)

в)

2. Якщо функції і диференційовані в точці х, то їхній добуток також – диференційована функція в цій точці і , або коротко говорять: похідна добутку двох функцій дорівнює сумі добутків кожної функції на похідну другої функції.

Наслідки

а) Постійний множник винести за знак похідної:

.

б) Похідна добутку декількох множників дорівнює сумі добутків похідної кожного із них на всі останні, наприклад:

.

Приклад. Знайдіть похідні функцій:

а)

б)

в)

Розв’язання

а)

б)

в)

3. Якщо функція і диференційовані в точці х і , то функція диференційована в цій точці і

Приклад. Знайдіть похідну функцій

а) б)

Розв’язання

а)

б)

4. У складеній функції присутня проміжна змінна . Тому при знаходженні похідної складеної функції ми будемо вказувати, по якій змінній взято похідну, використовуючи при цьому спеціальні позначення:

- похідна функції у по аргументу х;

- похідна функції у по аргументу и;

- похідна функції и по аргументу х.

Похідна складеної функції знаходиться за формулою

, де ,

Або похідна складеної функції дорівнює похідній зовнішній функції по проміжній змінній, помноженій на похідну внутрішньої функції по основному аргументу.

Приклад . Знайдіть похідну функції .

Розв’язання

- складена функція , де , тоді , .

При обчисленні похідної складеної функції явне введення допоміжної букви и для позначення проміжного аргументу не є обов’язковим. Тому похідну даної функції знаходять відразу як добуток похідної степеневої функції на похідну від функції ;