61. Электромагнитные волны в проводниках. Скин-эффект.

ЭМП в проводниках. Скин-эффект

Если , то в , 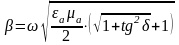можно пренебречь «1»:

; откуда следует

. (9.1)

Анализ показывает, что при высоких частотах коэффициент затухания в проводнике достигает значительных величин ( пропорционален ). Соответственно глубина проникновения ЭМП в проводник () составляет мкм (УВЧ) и мм (на ВЧ). Таким образом, ЭМП в проводник не проникает, концентрируясь в тонком поверхностном слое, называемом скин-слоем. Данное явление называют скин-эффектом (skin (англ.) – оболочка, кожа).

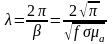. (9.2) 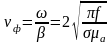. (9.3)

При прохождении в проводнике расстояния равного  ЭМВ испытывает очень большое затухание . Поэтому можно говорить о том, что пространственная периодичность поля плоской ЭМВ в проводнике отсутствует . v_гр0.

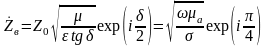. (9.4)

Волновое сопротивление проводника имеет примерно одинаковые по модулю активную и реактивную части, поскольку при tg>10 для проводников >84. Комплексное волновое сопротивление проводника имеет индуктивный характер, поскольку отстает по фазе от на 45.

Например, для меди (Приложение 3) при частоте ЭМП 1МГц (₀=300м) получаем: ==1,510⁴(1/м), v_ф=420 (м/с), =4,210^-4(м), =67(мкм), v_гр=0, Z_c=3,710^-4exp(-i/4) (Ом)

Сопротивление проводников на высоких частотах

В случае постоянного тока сопротивление проводника цилиндрической формы можно описать формулой (a – радиус проводника):

. (9.5)

На высоких частотах (при сильном скин-эффекте) ЭМП концентрируется в тонком поверхностном слое, что приводит к уменьшению площади сечения проводника (S_экв = S₀ – S_вн), по которой протекает ток:

. (9.6)

Обобщая (9.6) для проводника с произвольной формой сечения, получим:

, (9.7)

где p_r – периметр поперечного сечения проводника.

62.Свойства плоских электромагнитных волн. Связь между полями e и h , волновым вектором k и частотой w .

Напомним, что если в электромагнитной волне вектор  имеет единственное направление (а, следовательно, единственное на­правление имеет и вектор ), то волна называется линейно-поляризованной. Ниже будут приведены доказательства того, что свет представляет собой электромагнитные волны,  частоты которых лежат в определенном интервале. Если в световой волне вектор  (и ) имеет всевозможные направления,  то такой свет принято называть естественным. Следовательно, свет как плоская электромагнитная волна может быть в однородной среде как естественным, так и линейно-поляризованным.

Электромагнитная волна может переносить электромагнитную энергию (поток энергии). Вычислим поток электромагнитной энергии в вакууме, исходя из уравнений Максвелла. Для этого умножим обе стороны уравнения (12.1) скалярно на , а обе стороны  уравнения (12.2) – на :

,                                                                      (12.18)

.                                                                                   (12.19)

Используем формулу векторного анализа

и, соответственно, вычтем из уравнения (12.18) выражение (12.19):

.                                                            (12.20)

Выражение (12.20) представляет собой запись закона сохранения энергии электромагнитного поля в дифференциальной форме. Рассмотрим физический смысл отдельных величин, входящих в уравнение (12.20). Частная производная  представляет собой приращение электромагнитной энергии единицы объема за единицу времени, a  – поток энергии, вытекающей из единицы объема за единицу времени. Вектор  представляет собой поток энергии через единичную площадку, расположенную перпендикулярно потоку. При  и  поток постоянен и вектор  выражает поток энергии за единицу времени, при переменных  и  он выражает мгновенное значение потока.

Введем обозначение:

,                                                                                                  (12.21)

где  называют вектором Умова–Пойнтинга. Этот вектор определяет направление распространения энергии волны.

Вычислим вектор Умова–Пойнтинга плоской электромагнитной волны:

.                                                                               (12.22)

Согласно выражению (12.22), векторы S и k коллинеарны. Это справедливо только для вакуума и изотропных сред. В анизотропных средах, в которых физические свойства различны для разных направлений, это условие в общем случае не выполняется. Используем ранее введенный единичный вектор m, направленный вдоль распространения волны .

Поскольку для вакуума  то

.                                                                                       (12.23)

Найдем соотношение между абсолютными  значениями векто­ров  и  в плоской волне. Из уравнений (12.15) и (12.16) имеем:

.                                                                                  (12.24)

Имея в виду, что , получим:

.                                                                                   (12.25)

Учитывая, что векторы , ,  взаимно перпендикулярны, находим соотношение между  абсолютными значениями векторов  и :

.                                                                                             (12.26)

Из общего определения плотности электромагнитной энергии в вакууме

.                                                                                             (12.27)

С учетом уравнения (12.11) для плоской волны получим

.                                                                                             (12.28)

Запишем теперь окончательное выражение для вектора Умова–Пойнтинга в плоской волне:

.                                                                           (12.29)

Полученное равенство имеет простой смысл. Через единичную площадку, поставленную перпендикулярно распространению волны, в единицу времени проходит энергия, заключенная в цилиндре с площадью основания, равной единице, и высотой .

63………