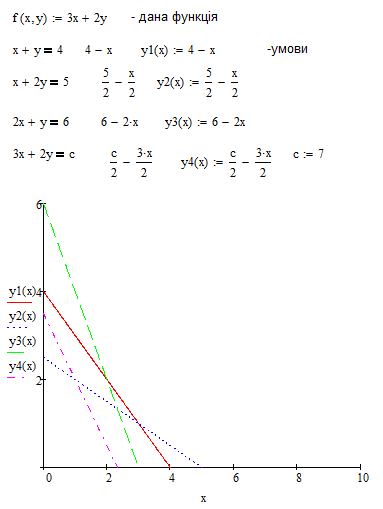
Регресія

Регре́сія (англ. regression, нім. Regression f, рос. регрессия) — форма зв'язку між випадковими величинами. Закон зміни математичного очікування однієї випадкової величини залежно від значень іншої. Розрізняють прямолінійну, криволінійну, ортогональну, параболічну та інші регресії, а також лінію і площину регресії.

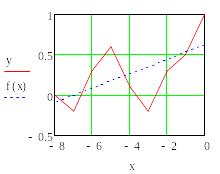
Інтерполяція

Інтерполяція — в обчислювальній математиці спосіб знаходження проміжних значень величини за наявним дискретним набором відомих значень.

Багатьом із тих, хто стикається з науковими та інженерними розрахунками часто доводиться оперувати наборами значень, отриманих експериментальним шляхом чи методом випадкової вибірки. Як правило, на підставі цих наборів потрібно побудувати функцію, зі значеннями якої могли б з високою точністю збігатися інші отримувані значення. Така задача називається апроксимацією кривої. Інтерполяцією називають такий різновид апроксимації, при якій крива побудованої функції проходить точно через наявні точки даних.

Існує також близька до інтерполяції задача, що полягає в апроксимації якої-небудь складної функції іншою, простішою функцією. Якщо деяка функція занадто складна для продуктивних обчислень, можна спробувати обчислити її значення в декількох точках, а за ними побудувати, тобто інтерполювати, простішу функцію. Зрозуміло, використання спрощеної функції не дозволяє одержати такі ж точні результати, які давала б початкова функція. Але, для деяких класів задач, досягнутий виграш у простоті і швидкості обчислень може переважити отриманий огріх у результатах.

Графіки функцій

Графік функції у неявній формі

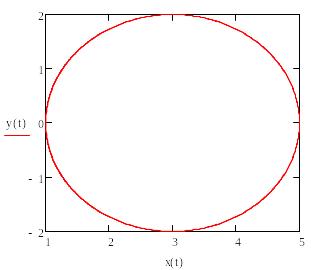
Графік функції у параметричній формі

Графік функції у явній формі

Визначення найбільшого і найменшого значення фунції

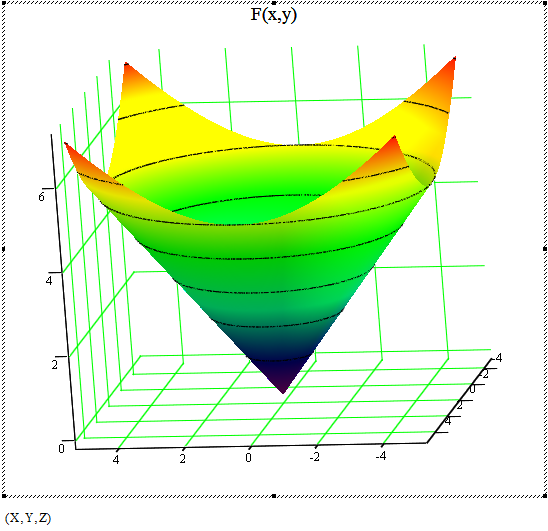
Графіки поверхонь

Графік поверхні у декартовій системі координат

Графік поверхні у сферичній системі координат

Matlab

Табулювання функції

Табулювання функції – це складання таблиці, у якій для кожного значення аргументу обчислено відповідне значення функції.

1.

a=4.1;

b=2.7;

x=1.2:0.8:5.2;

y=(a.*sqrt(x)-b.*(log(x)/log(5)))/(log10(abs(x-1)));

C=[x y];

disp(C);

Виконання

ans =

1.2000 2.0000 2.8000 3.6000 4.4000 5.2000 5.7805

1.2000 2.0000 2.8000 3.6000 4.4000 5.2000 5.7805

2.

x(1)=1.9;

x(2)=2.15;

x(3)=2.34;

x(4)=2.73;

x(5)=3.16;

a=4.1;

b=2.7;

for x=1:5 y=(a.*sqrt(x)-b.*(log(x)/log(5)))/(log10(abs(x-1)))

end;

y =

0

y =

Inf

y =

17.4679

y =

12.3121

y =

10.7429

Пошук коренів методом Гауса

Ме́тод Га́уса — алгоритм розв'язку системи лінійних алгебраїчних рівнянь.

Прямий хід: Шляхом елементарних перетворень рядків (додавань до рядка іншого рядка, помноженого на число, і перестановок рядків) матриця приводиться до верхньотрикутного вигляду(ступінчатого вигляду).

З цього моменту починається зворотний хід.

З останнього ненульового рівняння виражаємо кожну з базисних змінних через небазисні і підставляємо в попередні рівняння. Повторюючи цю процедуру для всіх базисних змінних, отримуємо фундаментальний розв'язок.

>> a=[5 3 3 -4; -6 -4 2 17; 12 26 1 5; 5 8 9 7];

>> b=[7; -24; 34; -6];

>> C=[a b];

>> D=rref(C);

>> x=D(:,5)

x = - розв’язок

1.9618

0.5469

-1.9629

-0.3598