20. Связь коэффициентов обычной и стандартизованной регрессии.

Метод наименьших квадратов применим и к уравнению множественной регрессии в стандартизированном масштабе:

                                      (2.4)

где   – стандартизированные переменные:  ,  , для которых среднее значение равно нулю:  , а среднее квадратическое отклонение равно единице:  ;   – стандартизированные коэффициенты регрессии.

Стандартизованные коэффициенты регрессии показывают, на сколько единиц изменится в среднем результат, если соответствующий фактор   изменится на одну единицу при неизменном среднем уровне других факторов. В силу того, что все переменные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии   можно сравнивать между собой. Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат. В этом основное достоинство стандартизованных коэффициентов регрессии в отличие от коэффициентов «чистой» регрессии, которые несравнимы между собой.

Применяя МНК к уравнению множественной регрессии в стандартизированном масштабе, получим систему нормальных уравнений вида

                               (2.5)

где   и   – коэффициенты парной и межфакторной корреляции.

Коэффициенты «чистой» регрессии   связаны со стандартизованными коэффициентами регрессии   следующим образом:

          .                                                 (2.6)

Поэтому можно переходить от уравнения регрессии в стандартизованном масштабе (2.4) к уравнению регрессии в натуральном масштабе переменных (2.1), при этом параметр   определяется как

.

Рассмотренный смысл стандартизованных коэффициентов регрессии позволяет их использовать при отсеве факторов – из модели исключаются факторы с наименьшим значением  .

На основе линейного уравнения множественной регрессии

                          (2.7)

могут быть найдены частные уравнения регрессии:

                                         (2.8)

т.е. уравнения регрессии, которые связывают результативный признак с соответствующим фактором   при закреплении остальных факторов на среднем уровне. В развернутом виде систему (2.8) можно переписать в виде:

21. Показатели силы связи в модели множественной регрессии.

К соизмеримым показателям тесноты связи относятся:

1) коэффициенты частной эластичности;

2) стандартизированные частные коэффициенты регрессии;

3) частный коэффициент детерминации.

Если факторные переменные имеют несопоставимые единицы измерения, то связь между ними измеряется с помощью соизмеримых показателей тесноты связи. С помощью соизмеримых показателей тесноты связи характеризуется степень зависимости между факторной и результативной переменными в модели множественной регрессии.

Коэффициент частной эластичности рассчитывается по формуле:

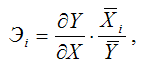
где

– среднее значение факторной переменной xi по выборочной совокупности,

– среднее значение результативной переменной у по выборочной совокупности;

– первая производная результативной переменной у по факторной переменной х.

Частный коэффициент эластичности измеряется в процентах и характеризует объём изменения результативной переменнойу при изменении на 1 % от среднего уровня факторной переменной xiпри условии постоянства всех остальных факторных переменных, включённых в модель регрессии.

Для линейной модели регрессии частный коэффициент эластичности рассчитывается по формуле:

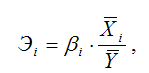
где ?i– коэффициент модели множественной регрессии.

Для того чтобы рассчитать стандартизированные частные коэффициенты регрессии, необходимо построить модель множественной регрессии в стандартном (нормированном) масштабе. Это означает, что все переменные, включённые в модель регрессии, стандартизируются с помощью специальных формул. Посредством процесса стандартизации точкой отсчёта для каждой нормированной переменной устанавливается её среднее значение по выборочной совокупности. При этом в качестве единицы измерения стандартизированной переменной принимается её среднеквадратическое отклонение?.

Факторная переменная х переводится в стандартизированный масштаб по формуле:

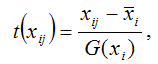
где xij – значение переменной xj в i-том наблюдении;

G(xj)  – среднеквадратическое отклонение факторной переменной xi;

Результативная переменная у переводится в стандартизированный масштаб по формуле:

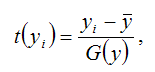
где G(y) – среднеквадратическое отклонение результативной переменной у.

Стандартизированные частные коэффициенты регрессии характеризуют, на какую долю своего среднеквадратического отклонения G(y) изменится результативная переменная у при изменении факторной переменной х на величину своего среднеквадратического отклонения G(x), при условии постоянства всех остальных факторных переменных, включённых в модель регрессии.

Стандартизированный частный коэффициент регрессии характеризует степень непосредственной или прямой зависимости между результативной и факторной переменными. Но в связи с тем, что между факторными переменными, включёнными в модель множественной регрессии, существует зависимость, факторная переменная оказывает не только прямое, но и косвенное влияние на результативную переменную.

Частный коэффициент детерминации используется для характеристики степени косвенного влияния факторной переменной х на результативную переменную у:

где ?i– стандартизированный частный коэффициент регрессии;

r(xixj) – коэффициент частной корреляции между факторными переменными xi и xj.

Частный коэффициент детерминации характеризует, на сколько процентов вариация результативной переменной вызвана вариацией i-ой факторной переменной, включённой в модель множественной регрессии, при условии постоянства всех остальных факторных переменных, включённых в модель регрессии.

Стандартизированные частные коэффициенты регрессии и частные коэффициенты эластичности могут давать различные результаты. Это несовпадение может быть объяснено, например, слишком большой величиной среднеквадратического отклонения одной из факторных переменных или эффектом неоднозначного воздействия одной из факторных переменных на результативную переменную.