
- •1.Эконометрика, её задача и метод.
- •2. Экономические данные и их статистические хараетристики.
- •3.Типовые распределения выборочных характеристик
- •4. Точность и надежность выборочных характеристик. Понятие надежности и доверительного интервала.
- •5. Корреляция случайных величин, уравнение регрессии. Регрессионная зависимость между случайными факторами.
- •6. Оценка параметров уравнения регрессии методом наименьших квадратов.
- •7. Геометрическая интерпретация метода наименьших квадратов.
- •8.Показатели адекватности уравнения регрессии
- •9. Связь дисперсии результирующей переменной с дисперсией регрессии
- •10. Связь дисперсии результирующей переменной с остаточной дисперсией
- •11. Точность и значимость коэффициентов регрессии.
- •12. Связь показателей адекватности и точности уравнения регрессии.
- •13. Связь коэффициентов уравнения регрессии с выборочными значениями результирующей переменной
- •14. Дисперсия коэффициентов регрессии.
- •15. Условия оптимальности мнк-оценок. Теорема Гаусса-Маркова.
- •16. Множественная линейная регрессия.
- •17. Решение системы линейных уравнений множественной регрессии
- •18. Матричная форма записи множественной линейной регрессии
- •19. Натуральная и стандартизованная формы модели множественной регрессии.
- •20. Связь коэффициентов обычной и стандартизованной регрессии.
- •21. Показатели силы связи в модели множественной регрессии.
- •22. Оптимальность коэффициентов множественной регрессии.
- •23. Оценка значимости модели множественной регрессии и ее параметров.
- •24. Прогнозирование на основе модели множественной регрессии.
- •25. Линейные регрессионные модели с гетероскедастичностью.
- •26. Нелинейные регрессионные модели и их классификация.
- •27. Регрессионная модель, линейная относительно параметров.
- •28.Обобщенный метод наименьших квадратов
- •30. Особенности включения в модели регрессии неколичественных показателей.
- •31. Модели регрессии с фиктивными переменными сдвига, наклона.
- •32. Временной ряд и его характеристики.
- •33. Корреляция временных рядов.
- •34. Определение тренда временного ряда.
- •35. Учет автокорреляции остатков временного ряда. Критерий Дарбина-Уотсона.
- •36. Сглаживание временных рядов.
- •37. Системы эконометрических моделей. Одновременные системы уравнений.
- •38. Проблема идентификации эконометрических моделей.
5. Корреляция случайных величин, уравнение регрессии. Регрессионная зависимость между случайными факторами.
Прямое токование термина корреляция — стохастическая, вероятная, возможная связь между двумя (парная) или несколькими (множественная) случайными величинами.
Выше говорилось о том, что если для двух СВ (X и Y) имеет место равенство
P(XY)
=P(X) ![]() P(Y),
P(Y),
то величины X и Y считаются независимыми. Ну, а если это не так!?
Ведь всегда важен вопрос — а как сильно зависит одна СВ от другой? И дело в не присущем людям стремлении анализировать что-либо обязательно в числовом измерении. Уже понятно, что системный анализ означает непрерывные выЧИСЛения, что использование компьютера вынуждает нас работать с числами, а не понятиями.
Для числовой оценки возможной связи между двумя случайными величинами: Y(со средним My и среднеквадратичным отклонением Sy) и — X (со средним Mx и среднеквадратичным отклонением Sx) принято использовать так называемый коэффициент корреляции
Rxy=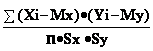 .
{2 - 11}
.
{2 - 11}
Этот коэффициент может принимать значения от -1 до +1 — в зависимости от тесноты связи между данными случайными величинами.
Если коэффициент корреляции равен нулю, то X и Y называют некоррелированными. Считать их независимыми обычно нет оснований — оказывается, что существуют такие, как правило — нелинейные связи величин, при которых Rxy = 0, хотя величины зависят друг от друга. Обратное всегда верно — если величины независимы, тоRxy = 0. Но, если модуль Rxy = 1, то есть все основания предполагать наличие линейной связи между Y и X.Именно поэтому часто говорят о линейной корреляции при использовании такого способа оценки связи между СВ.
Отметим еще один способ оценки корреляционной связи двух случайных величин — если просуммировать произведения отклонений каждой из них от своего среднего значения, то полученную величину —
Сxy= S (X - Mx)·(Y - My)
или ковариацию величин X и Y отличает от коэффициента корреляции два показателя: во-первых, усреднение (деление на число наблюдений или пар X, Y) и, во-вторых, нормирование путем деления на соответствующие среднеквадратичные отклонения.
Такая оценка связей между случайными величинами в сложной системе является одним из начальных этапов системного анализа, поэтому уже здесь во всей остроте встает вопрос о доверии к выводу о наличии или отсутствии связей между двумя СВ.
В современных методах системного анализа обычно поступают так. По найденному значению R вычисляют вспомогательную величину:
W = 0.5 Ln[(1 + R)/(1-R)] {2 - 12}
и вопрос о доверии к коэффициенту корреляции сводят к доверительным интервалам для случайной величины W,которые определяются стандартными таблицами или формулами.
В отдельных случаях системного анализа приходится решать вопрос о связях нескольких (более 2) случайных величин или вопрос о множественной корреляции.
Пусть X, Y и Z - случайные величины, по наблюдениям над которыми мы установили их средние Mx, My,Mz и среднеквадратичные отклонения Sx, Sy, Sz.
Уравнение регрессии
Регрессия (лат. regressio - обратное движение, переход от более сложных форм развития к менее сложным) - одно из основных понятий в теории вероятности и математической статистике, выражающее зависимость среднего значения случайной величины от значений другой случайной величины или нескольких случайных величин.
y=f(x) - уравнение регрессии - это формула статистической связи между переменными.
Одним
из элементов конкретных исследований
является сопоставление различных
уравнений зависимости, основанное на
использовании критериев качества
аппроксимации эмпирических данных
конкурирующими вариантами моделей
Наиболее часто для характеристики
связей экономических показателей
используют следующие типы
функций:
1. Линейная: ![]() 2. Гиперболическая:
2. Гиперболическая: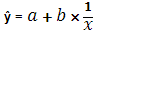 3. Показательная:
4. Параболическая:
3. Показательная:
4. Параболическая: ![]() 5. Степенная:
5. Степенная: ![]() 6. Логарифмическая:
6. Логарифмическая:![]() 7. Логистическая:
7. Логистическая: ![]() [2, c.258]
Модель
с одной объясняющей и одной объясняемой
переменными – модель парной регрессии.
Если объясняющих (факторных) переменных
используется две или более, то говорят
об использовании модели множественной
регрессии. При этом, в качестве вариантов
могут быть выбраны линейная,
экспоненциальная, гиперболическая,
показательная и другие виды функций,
связывающие эти переменные.
Для
нахождения параметров а и b уравнения
регрессии используют метод наименьших
квадратов. При применении метода
наименьших квадратов для нахождения
такой функции, которая наилучшим образом
соответствует эмпирическим данным,
считается, что сумка квадратов отклонений
эмпирических точек от теоретической
линии регрессии должна быть величиной
минимальной.
[2, c.258]
Модель
с одной объясняющей и одной объясняемой
переменными – модель парной регрессии.
Если объясняющих (факторных) переменных
используется две или более, то говорят
об использовании модели множественной
регрессии. При этом, в качестве вариантов
могут быть выбраны линейная,
экспоненциальная, гиперболическая,
показательная и другие виды функций,
связывающие эти переменные.
Для
нахождения параметров а и b уравнения
регрессии используют метод наименьших
квадратов. При применении метода
наименьших квадратов для нахождения
такой функции, которая наилучшим образом
соответствует эмпирическим данным,
считается, что сумка квадратов отклонений
эмпирических точек от теоретической
линии регрессии должна быть величиной
минимальной.
Корреляционная
зависимость — статистическая взаимосвязь
двух или несколькихслучайных
величин (либо
величин, которые можно с некоторой
допустимой степенью точности считать
таковыми). При этом изменения значений
одной или нескольких из этих величин
сопутствуют систематическому изменению
значений другой или других
величин.[1] Математической
мерой корреляции двух случайных величин
служит корреляционное
отношение ![]() [2],
либо коэффициент
корреляции
[2],
либо коэффициент
корреляции ![]() (или
(или ![]() )[1].
В случае, если изменение одной случайной
величины не ведёт к закономерному
изменению другой случайной величины,
но приводит к изменению другой
статистической характеристики данной
случайной величины, то подобная связь
не считается корреляционной, хотя и
является статистической.
)[1].
В случае, если изменение одной случайной
величины не ведёт к закономерному
изменению другой случайной величины,
но приводит к изменению другой
статистической характеристики данной
случайной величины, то подобная связь
не считается корреляционной, хотя и
является статистической.
