35. Учет автокорреляции остатков временного ряда. Критерий Дарбина-Уотсона.
Критерий Дарбина—Уотсона (или DW-критерий) — статистический критерий, используемый для тестирования автокорреляции первого порядка элементов исследуемой последовательности. Наиболее часто применяется при анализе временных рядов и остатков регрессионных моделей.
Критерий
Дарбина—Уотсона неприменим для
моделей авторегрессии,
так как он для подобного рода моделей
может принимать значение, близкое к
двум, даже при наличии автокорелляции
в остатках. Для этих целей
используется 
-критерий
Дарбина.
-статистика
Дарбина применима тогда, когда среди
объясняющих регрессоров есть 
.
На первом шаге методом МНК строится
регрессия. Затем критерий
Дарбина
применяется для выявления автокорреляции
остатков в модели с распределёнными
лагами[2]:
где
—
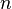число наблюдений
в модели;
—
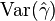оценка дисперсии
коэффициента при лаговой результативной
переменной
.
При увеличении объёма выборки распределение -статистики стремится к нормальному с нулевым математическим ожиданием и дисперсией, равной 1. Поэтому гипотеза об отсутствии автокорреляции остатков отвергается, если фактическое значение -статистики оказывается больше, чем критическое значение нормального распределения[3].
Ограничение данной статистики следует из её формулировки: в формуле присутствует квадратный корень, следовательно, если дисперсия коэффициента при велика, то процедура невыполнима.
36. Сглаживание временных рядов.
Выравнивание временных рядов [time-series smoothing] — выявление основной тенденции развития (временнóго тренда) путем «очистки» временного ряда от искажающих эту тенденцию случайных отклонений. Предполагается, что каждый член ряда состоит из двух компонент: уровня ut и случайного отклонения от него et:
ut = ut + et
Слагаемое ut отражает существенные и типичные черты развития системы, отражаемые анализируемым временным рядом, т.е. последовательными значениями соответствующего экономического показателя. Случайные же отклонения мешают выявить основную тенденцию развития. Наглядным и простым способом выравнивания ряда является фиксация точек на графике и проведение на глаз плавной кривой между ними (и возле них), выражающей исконную тенденцию (рис.В.6).
Такой способ дает приблизительные результаты, иногда все же достаточные для анализа. Однако в сложных случаях применяются математико-статистические методы выравнивания; расчеты при этом ведутся на компьютерах. В частности, с помощью метода наименьших квадратов, сплайн-функции, методов скользящейсредней, экспоненциального сглаживания,аналитического выравнивания и др.
