25. Линейные регрессионные модели с гетероскедастичностью.

Линейная регрессия (англ. Linear regression) — используемая в статистике регрессионная модель зависимости одной (объясняемой, зависимой) переменной y от другой или нескольких других переменных (факторов, регрессоров, независимых переменных) x с линейной функцией зависимости.

Модель линейной регрессии является часто используемой и наиболее изученной в эконометрике. А именно изучены свойства оценок параметров, получаемых различными методами при предположениях о вероятностных характеристиках факторов, и случайных ошибок модели. Предельные (асимптотические) свойства оценок нелинейных моделей также выводятся исходя из аппроксимации последних линейными моделями. Необходимо отметить, что с эконометрической точки зрения более важное значение имеет линейность по параметрам, чем линейность по факторам модели.

Регрессионная модель

,

где   — параметры модели,   — случайная ошибка модели, называется линейной регрессией, если функция регрессии   имеет вид

,

где   — параметры (коэффициенты) регрессии,   — регрессоры (факторы модели), k — количество факторов модели.

Коэффициенты линейной регрессии показывают скорость изменения зависимой переменной по данному фактору, при фиксированных остальных факторах (в линейной модели эта скорость постоянна):

Параметр  , при котором нет факторов, называют часто константой. Формально — это значение функции при нулевом значении всех факторов. Для аналитических целей удобно считать, что константа — это параметр при «факторе», равном 1 (или другой произвольной постоянной, поэтому константой называют также и этот «фактор»). В таком случае, если перенумеровать факторы и параметры исходной модели с учетом этого (оставив обозначение общего количества факторов — k), то линейную функцию регрессии можно записать в следующем виде, формально не содержащем константу:

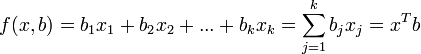
 — вектор регрессоров,   — вектор-столбец параметров (коэффициентов)

Линейная модель может быть как с константой, так и без константы. Тогда в этом представлении первый фактор либо равен единице, либо является обычным фактором соответственно.

ГЕТЕРОСКЕДАСТИЧНОСТЬ [heteroscedasticity] (неоднородность) — понятие математической статистики иэконометрии; означает ситуацию, когда дисперсия ошибки в уравнении регрессии изменяется от наблюдения к наблюдению. В этом случае приходится подвергать определенной модификации метод наименьших квадратов(иначе возможны ошибочные выводы).

26. Нелинейные регрессионные модели и их классификация.

Нелинейные регрессионные модели — модели вида

которые не могут быть представлены в виде скалярного произведения

где   — параметры регрессионной модели,   — свободная переменная из пространства  ,   — зависимая переменная,   — случайная величина и   — функция из некоторого заданного множества.

Значения параметров в случае нелинейной регрессии находят с помощью одного из методов градиентного спуска, например алгоритма Левенберга-Марквардта.

Нелинейная модель. уравнение зависимости между Уи Х может быть представлено степенной функцией У от Х,  , показательной  , гиперболической   и д. р.

Для оценки параметров в этих случаях метод наименьших квадратов можно применять после логарифмирования, либо после введения новой переменной.

Для показательной функции:

ln y=ln a+x ln b

Y α β

Y = α + х β Þ а = еα; b=еβ

Для степенной функции

ln y=ln a+b ln x

Y α X

Y = α + β X

Для гиперболической функции

у=а+b/x

1/х=Х

У=а+bХ

Нелинейные модели регрессии и их линеаризация.

Регрессии нелинейные по объясняющим переменным, но линейные по оценивающим параметрам – для расчета параметров нелинейной регрессии применяется метод наименьших квадратов, после предварительной процедуры линеаризации функции регрессии. Приводятся к линейным путем замены переменных. Нелинейная регрессия y = a + b*ln(x) приводится к линейной y = a + bx', где x' = ln(x). Регрессии нелинейные по оценивающим параметрам:

• нелинейные модели внутри линейных (приводятся к линейному виду);

• нелинейные модели внутри нелинейных.

Для оценки параметров нелинейной модели используется два подхода:

• линеаризация модели (с помощью преобразований исходных переменных исследуемую зависимость представляют в виде линейного соотношения);

• методы нелинейной оптимизации (применяются когда подобрать линеаризирующее преобразование не получается).