16. Методы сравнения проектов с разными сроками осуществления.
Модификация метода npv для сравнения проектов с разными сроками функционирования
В практике анализа инвестиционных проектов находят применение два подхода к выбору проектов с неравными сроками: метод продолженного срока и метод эквивалентного ежегодного аннуитета.
Метод продолженного срока предполагает возможность повторного осуществления проектов и использование критерия выбора NPV (по наибольшему значению) для многоразового осуществления проектов.
Рассмотрим проекты А1 и А2 с неравными сроками функционирования (табл. 9).
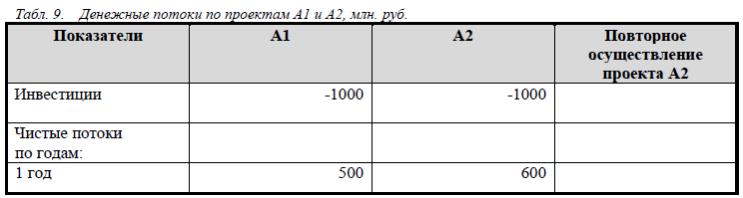
NPV проекта А1 больше, чем проекта А2, но выбор проекта А2 дает возможность осуществить еще один проект за рассматриваемый временной промежуток осуществления проекта А1. Двухразовое осуществление проекта А2 дает большее значение NPV. Следовательно, проект А2 предпочтительнее (предполагается возможность двухразового осуществления проекта при неизменной стоимости капитала, инвестициях и отдаче).
Метод продолженного срока предполагает:
1) нахождение наименьшего общего кратного для числа лет функционирования двух или нескольких оцениваемых проектов (например, при выборе из двух альтернативных проектов, рассчитанных на 2 и 3 года, продолженный срок функционирования равен 6 годам, один проект осуществится по данному методу два раза, а другой три раза);
2) расчет NPV многоразового осуществления каждого проекта на продолженном сроке NPV (i, n), где i — срок функционирования проекта, n -число реализаций проекта, продолженный срок равен произведению i х n;
3) выбор проекта с наибольшим значением NPV.
Например, рассматриваются проекты С1 и С2 с равными инвестиционными затратами в году t = 0 и чистыми денежными потоками, представленными на рис. 8.
При стоимости капитала проекта 15% NPV по первому проекту (С1 с 3- летним сроком функционирования) равен 19,93. NPV проекта С2 = 6,7. Для сравнения проектов и выбора наилучшего следует найти продолженный срок для двух проектов. Срок функционирования первого проекта обозначим через i (i = 3), а второго j (j = 2). Наименьшее кратное равно 6 — это продолженный срок. Денежные потоки по проектам с учетом повтора изображены на рис. 9.
Двухразовое осуществление первого проекта (n1 = 2) дает значение NPV, равное 33. NPV(i, n1) = 19,93 + 19,93/1,153= 33.
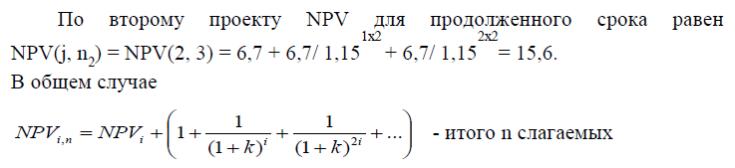
При большом числе слагаемых в формуле NPV(i, n), особенно если сравнивается много проектов, расчет может быть упрощен введением предположения о возможности неограниченного числа раз реализации проектов (n → ∞ по всем проектам). Предельное значение NPV по каждому проекту на продолженном сроке функционирования может быть найдено по формуле:
Метод эквивалентного ежегодного аннуитета предполагает:
1) расчет NPV по каждому проекту с индивидуальным сроком функционирования (NPVi);
2) нахождение денежного потока в виде аннуитета, который на индивидуальном сроке функционирования обеспечивал бы то же значение NPV. Правило метода — проект с более высоким эквивалентным аннуитетом для любого срока функционирования обеспечит более высокое значение NPV, и такой проект предпочтительнее;
3) анализ может быть продолжен расчетом NPV по каждому проекту для бесконечного аннуитета. Если X— чистый денежный поток по аннуитету (возникает через равные промежутки времени в неизменном количестве), то NPV бессрочного аннуитета равен Х/k, где k — стоимость капитала. Правило метода — наибольшее значение NPV для бессрочного аннуитета характеризует лучший проект. Рассмотрим использование метода для проектов А1 и А2, рассчитанных соответственно на 4 и 2 года (см. табл. 10 и рис. 10).
По правилу наибольшего значения аннуитета проект А2 предпочтительнее. В этом можно убедиться, рассчитав и NPV бесконечного аннуитета. NPV проекта А2 составляет 23,63/ 0,1 = 236,3. NPV проекта А1 - 14,2 /0,1 =142. Рассмотренные два метода имеют ограничения:
1) если учесть инфляцию, то может оказаться, что повторное осуществление проекта обойдется дороже, чем прогнозируется при одноразовом осуществлении;
2) для проектов с длительным функционированием реально спрогнозировать срок довольно сложно и возможны погрешности. При большом значении наименьшего кратного и множестве проектов расчеты сильно усложняются. На практике, если рассматриваются, например, проекты со сроком функционирования 11 и 7 лет, которые имеют стандартные денежные потоки, то ограничиваются расчетом NPV для 7 лет или сравнением аннуитетов.
17. Методика расчета и экономический смысл показателя рентабельности инвестиций.
Смотреть вопрос 6
22. Методика расчета и экономический смысл показателя «чистая приведенная стоимость» (NPV).
Метод расчета чистого дисконтированного (приведенного) дохода (Net Present Value, NPV), который основан на сопоставлении величины исходных инвестиций (I, Invested Capital) с общей суммой дисконтированных чистых денежных поступлений, генерируемых ими в течение прогнозного периода, и характеризует современную величину эффекта от будущей реализации инвестиционного проекта. Поскольку приток денежных средств распределен во времени, он дисконтируется посредством коэффициента r, который инвестор устанавливает сам, исходя из приемлемого для инвестирования капитала ежегодного процента возврата.
NPV является прибылью от проекта за вычетом цены денег и доплаты за риск.
Общая накоплена величина дисконтированных доходов (Present Value – PV – Приведенная стоимость) и чистый дисконтированный доход (Net Present Value - NPV) соответственно рассчитываются по формулам:
;
,
где DK - приток денежных средств (или CF (англ, cash flow) );
I - сумма начальных инвестиций (затраты);
r - коэффициент (ставка) дисконтирования;
n – время реализации проекта.
В приведенных здесь и далее формулах расчет начинается с k=1, поскольку условно считается, что на шаге 0 принимается решение, а изменение затрат и выгод по проекту начинается с шага 1 в зависимости от принятого решения.
Если вложения, связанные с предстоящей реализацией проекта, осуществляют в несколько этапов (ряда лет) (интервалов – m лет), то расчет показателя NPV производят по следующей формуле:
где m - продолжительность процесса инвестиций;
n - продолжительность периода отдачи от инвестиций.
Таким образом, метод чистой текущей стоимости (NPV) состоит в следующем.
Определяется текущая стоимость затрат (I), т.е. решается вопрос, сколько инвестиций нужно зарезервировать для проекта.
Рассчитывается текущая стоимость будущих денежных поступлений от проекта, для чего доходы за каждый год DK (кеш-флоу) приводятся к текущей дате.
Текущая стоимость инвестиционных затрат (I) сравнивается с текущей стоимостью доходов (PV). Разность между ними составляет чистую текущую стоимость доходов (NPV): NPV = PV – I.
NPV показывает чистые доходы или чистые убытки инвестора от помещения денег в проект, по сравнению с хранением денег в банке.
Если NPV > 0, то можно считать, что инвестиция приумножит богатство предприятия и проект следует принять.
При NPV < 0, то доходы от предложенной инвестиции недостаточно высоки, чтобы компенсировать риск, присущий данному проекту (или с точки зрения цены капитала не хватит денег на выплату дивидендов и процентов по кредитам) и инвестиционное предложение должно быть отклонено.
При NPV = 0 - проект ни прибыльный, ни убыточный. В случае реализации такого проекта благосостояние собственников предприятия не изменится, однако объемы производства возрастут. Поскольку часто увеличение производственного потенциала предприятия оценивается положительно, проект все же принимается.