15. Критерій Неймана-Пірсона

: Ө = ; ξ – абс. Неперервна p (x, ) (x)

: Ө = ; ξ –має щільність p (x, ) (x)

(x) dx

(x) dx

Для будь-якого α є [0,1] існує критична точка і E є [0,1] такі, що

Визначає оптимальний критерій з рівнем значущості α.

Дов : Розглянемо ф-ію від С

g (c) = P { (ѯ)>c (ѯ)}=P{ > c } – додаткова ф-ція розподілу для вв

g(+ )=0; g(0)=1

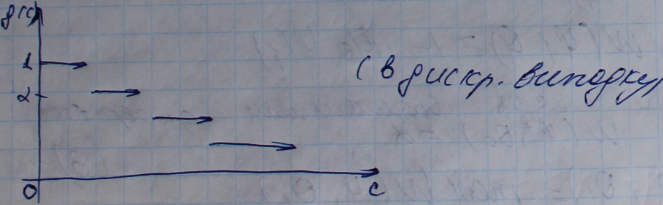
g( ) ≤ α<g(

і якщо g(c) = α для цілого інтервала [с1,с2] тоді в якості візьмемо будь-яку g цього інтервалу

Тоді E знайдемо так:

=

Якщо g ( -0)=g( , тоді = 0

А тепер доведемо що одержаний (х) критерій є оптимальним. Передусім перевіримо чи він має рівень значущості α :

Отже - критерій з рівнем значущості

Розглянемо будь-який інший критерій з рівнем знач.

M₁

Розглянемо інтеграл:

, тобто викон (3) => критерій - оптимальний.