
- •1.Характеристичні функції, властивості.
- •3.Цгт для однаково розподілених випадкових величин
- •4.Основні задачі. Вибірковий метод
- •5. Емпірична функція розподілу(ерф). Відхилення емпіричної функції розподілу від теоретичної
- •6. Вибірковий моменти, зв'язок з теоретичними моментами. Асимптотична поведінка вибіркових моментів
- •7. Статистика, оцінка, незміщені і спроможні оцінки
- •8. Статистичні оцінки для математичного сподівання, дисперсії і моментів
- •Незміщений:
- •9.Ефективні оцінки. Означення, Лема
- •10.Теорема Крамера-Рао
- •11.Методи одержання оцінок
- •12.Інтервальні оцінки, довірча область, надійність.
- •В залежності від того, по скільки складений є вираз в лівій частині буде залежати знайдений довірчий інтерв. Для θ чи ні.
- •13.Поняття статистичної гіпотези, статистичного критерію. Помилки першого і другого роду.
- •14.Рівень значущості критерію. Функція потужності критерія.
- •15. Критерій Неймана-Пірсона
12.Інтервальні оцінки, довірча область, надійність.
Всі
оцінки
які ми знаходили досі були точками (н)
:
є (н) с
 – основні точки.
– основні точки.
При реалізації вибірки в кожному випадку ми одержуємо різне значення оцінки , тому досить часто цікавляться не оцінкою , а областю S c (н) із заданою точністю.
Оскільки S будемо будувати за статист. Даними, тому ця область також є випадковою. Тому можна застосувати поняття : яка ймов. Що ця область містить невід. пер. θ.
Озн. Якщо будь яка область S, яка з ймов. Не менше α містить параметр θ, то вона називається довірчою областю, α –найдійність.
θ є R – одновимірний параметр.
Тоді в якості S буде виступати інтервал ( н, в)
Тоді Р { Ө ( н, в)} = α
Щоб довірчий інтеграл був знайдений однозначно накладаються умови:
P { θ ≤ н } = P{ θ ≥ в } = α /2
Якщо ( - θ)< δ, то δ називають точністю точкової оцінки.
P{( - θ)< δ} = α
Розглянемо деякі способи побудови довірчивої області
Якщо є велика к-сть статестичних даних : ξ 1… ξ n, - n –велике
f (ξ, θ)=L(θ) – випадкова величина
f(ξ 1… ξ n, θ)
Нехай виконуються умови леми, яка передувала т-мі крамер. Тоді
f
(ξ,
θ)
=
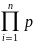 (ξ
і, θ)
(ξ
і, θ)

P{
|Ƞ| <
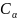 }=
α
}=
α
В залежності від того, по скільки складений є вираз в лівій частині буде залежати знайдений довірчий інтерв. Для θ чи ні.
13.Поняття статистичної гіпотези, статистичного критерію. Помилки першого і другого роду.
Припустимо
що випадкова величина ѯ має розп. G<
P=
{ ; Ө
є
}
; Ө
є
}
Озн1. Статистичною гіпотезою називається будь яке твердж. про розподіл або властивості розподілу, дослід. Випадкової величини
Напр.
Твердж. Розподіл досл. випадкової величини нормальний є статитс. гіпот. Часто розподіл bb нам відомий, а ми висуваємо гіпотези стосовно значення параметрів такі гіпотези назив. параметричними.
Озн2.
Статистична гіпотеза називається
простою , якщо вона полягає в тому, що
параметр рівний якомусь конкретному
числу. Гіпотеза називається складною
якщо в ній припускається параметр θ
< <
(
<
( ),
що складається більше ніж з однієї
точки.
),
що складається більше ніж з однієї
точки.
Озн3.
Статистична гіпотеза, яка має піддатися
перевірці познач.
 і назив. основною або нульовою гіпотезою.
Поряд з основною можуть розглядати одну
або декілька алотер. Гіпотез.
і назив. основною або нульовою гіпотезою.
Поряд з основною можуть розглядати одну
або декілька алотер. Гіпотез.
Озн4. Статистичний критерій перевірки гіпотези. Це правило, згідно якого гіпотезу будемо приймати або будемо відкидати. Якщо була гіпотезою про вигляд розподілу, то такий статистичний критерій називається критерієм узгодження. Поки що будемо вивчати парам.-гіп. І крит. перев. таких гіпотез.
Щоб дійти до висновку про відношення чи не відношення гупотези , треба вилучити у вибірковому просторі певну множину S, що як тільки стат. Дані потрапили в S, то гіпот. відхиляємо.
Розглянемо так звані помилки які можуть виникнути ( 1-го та 2-го роду)
Озн5 Помилкою 1-го роду називають помилку яка (велика є) полягає у відхиленні справ. гіпотези, 2-го роду , якщо крит. неспр. гіпотеза.
14.Рівень значущості критерію. Функція потужності критерія.
Озн 1
 p
(
p
( ,
,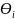 )
dx, і=0,1
)
dx, і=0,1
Тоді
α
=
 (S)=P{
ξ
є B
\
(S)=P{
ξ
є B
\
 }
– ймов. помилки 1-го роду
}
– ймов. помилки 1-го роду
α ще назив. рівнем значущості S – критеріїв
 P(S(заперечене))=P
(
ξ
є
S(заперечене)\
P(S(заперечене))=P
(
ξ
є
S(заперечене)\ – ймов. Помилки 2-го роду
– ймов. Помилки 2-го роду
S(заперечене)= X\S
1. Задали рівень значущості α
2.
 – розглянемо
множину усіх критеріїв з рівним значущості
α
– розглянемо
множину усіх критеріїв з рівним значущості
α
3. Серед усіх цих множин треба знайти ту для якої бета буде найменше.
Озн 2
Функцією
потужності S
– критеріїв
назив. W
(S,
 )
= S
p(x,
Ө)dx
)
= S
p(x,
Ө)dx
α
= W(S, )
)
 =1-
W(S,
=1-
W(S,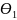 )
)
Серед усіх вибираємо той критерій S*:
W(S*, )= max W(S, ) (2)
S* що задовольняє (2) називається оптимальним або найбільш потужним критерієм.
