
- •1.Характеристичні функції, властивості.
- •3.Цгт для однаково розподілених випадкових величин
- •4.Основні задачі. Вибірковий метод
- •5. Емпірична функція розподілу(ерф). Відхилення емпіричної функції розподілу від теоретичної
- •6. Вибірковий моменти, зв'язок з теоретичними моментами. Асимптотична поведінка вибіркових моментів
- •7. Статистика, оцінка, незміщені і спроможні оцінки
- •8. Статистичні оцінки для математичного сподівання, дисперсії і моментів
- •Незміщений:
- •9.Ефективні оцінки. Означення, Лема
- •10.Теорема Крамера-Рао
- •11.Методи одержання оцінок
- •12.Інтервальні оцінки, довірча область, надійність.
- •В залежності від того, по скільки складений є вираз в лівій частині буде залежати знайдений довірчий інтерв. Для θ чи ні.
- •13.Поняття статистичної гіпотези, статистичного критерію. Помилки першого і другого роду.
- •14.Рівень значущості критерію. Функція потужності критерія.
- •15. Критерій Неймана-Пірсона
6. Вибірковий моменти, зв'язок з теоретичними моментами. Асимптотична поведінка вибіркових моментів
Нехай ξ(𝜔)=( ξ1… ξn) – вибірка, ξ: –незалежні і однаково розподілені з функцією розподілу F(x) позначимо через αk – к-ий момент випадкової величини ξ.
Теоретичні моменти |
Вибіркові моменти |
αk≡ α1=𝜇ξ –мат. сподівання |
Ak≡ |
μk≡μ(ξ-𝜇1)k= 𝜇1=0;
𝜇2=Dξ=
|
A1= 𝜇k=
|
Реальний вибірковий момент
 =
=
 ;
;
 =
=
 (залежність ξ:=х)
(залежність ξ:=х)
Лема: Мат. сподівання і дисперсія вибіркового моменту к-го порядку сожна подати через теоретичні моменти, а саме:
𝜇
Ak=𝛼k
;
DAk=
 =(ξ1,…,
ξn),
ξi
– незалежність, однаково розподілених
вв.
=(ξ1,…,
ξn),
ξi
– незалежність, однаково розподілених
вв.
 =
=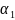 ,
,
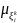 =
=
𝜇
Ak=𝜇
= ,
DAk=D
=
,
DAk=D
=
 =
= =(
=(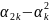 )/n.
)/n.
Теорема:
Нехай існує для ξ: α2k≡ <∞,
тоді випадкова величина Ak
<∞,
тоді випадкова величина Ak
 αk
αk
(за ймовірністю прямує до невідомого αk ) P: {|Ak – 𝛼k|>ε}=0
Дов.
За ймовірністю Липунова із існування
моментів порядку 2k
обов’язково буде випливати що утворюють
моменти нижчого порядку. Нагадаємо
ймовірність Чибешева для дисперсії:
P{|ξ–μξ|≥ε}≤ ;
∀ε>0
;
∀ε>0
За
нерівністю Чибишева: P{|Ak–αk|>ε}
= P{|Ak–𝜇Ak|>ε}
≤
 =
=
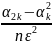
 0
0
Це
і означає що Ak αk
Отже,
насправді можна в якості найближчого
значення для αk
розглядати реальний вибірковий момент
ak.
Теорема:
Нехай
існують αm
< ∞. Тоді випадкова величина Ak
=
=
αk
Отже,
насправді можна в якості найближчого
значення для αk
розглядати реальний вибірковий момент
ak.
Теорема:
Нехай
існують αm
< ∞. Тоді випадкова величина Ak
=
= –
сума незалежних однаково розподілених
випадкових величин виду
–
сума незалежних однаково розподілених
випадкових величин виду
 μ
=
μ
=
 =
=

 =
=
 =
(
=
( )=
(
)
)=
(
)
За
ЦГТ у формі Лапласа P{ }
≈
Ф(x)
– функція розподілу N(0,1)
}
≈
Ф(x)
– функція розподілу N(0,1) Ak=
має
нормальний розподіл N(αk,
Ak=
має
нормальний розподіл N(αk,
 )
)
7. Статистика, оцінка, незміщені і спроможні оцінки
Нехай
функція розподілу дослідженої випадкової
величини ξ
належить
до деякої множини функцій розподілу
{F(x;𝜃);
𝜃
є Θ
ϲ
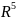 } 𝜃=(
} 𝜃=(
 …
…
 )
)
𝜃 – невідомий,
і ми мусимо його знайти маючи лише
реалізацію ( …
… )
вибірки
=(
)
вибірки
=( …
… )
визначити (оцінити) 𝜃
за
реалізацію це означає поставити у
відповідність реалізації (
…
)
число 𝜃,
тобто
нам потрібно побудувати функцію h(∙)
визначена на вибірковому просторі із
значенням в множині Θ,
і тоді
)
визначити (оцінити) 𝜃
за
реалізацію це означає поставити у
відповідність реалізації (
…
)
число 𝜃,
тобто
нам потрібно побудувати функцію h(∙)
визначена на вибірковому просторі із
значенням в множині Θ,
і тоді
 ≡
≡ h(ξ(ω))
h(ξ(ω))
Озн1:
Борелеву функцію h(∙)
задану на вибірковому просторі Х ϲ
 із
значенням в множині Θ (множина можливих
значень параметру 𝜃)
h: X→ Θ називається статистикою,
а
=
h(ξ(ω)) = h(
…
)
– оцінка
невідомого параметра 𝜃.
із
значенням в множині Θ (множина можливих
значень параметру 𝜃)
h: X→ Θ називається статистикою,
а
=
h(ξ(ω)) = h(
…
)
– оцінка
невідомого параметра 𝜃.
Для одного і того самого невідомого параметра 𝜃 можна запропонувати багато оцінок. Орієнтуватися будемо на те, наскільки великою є похибка при заміні невідомого 𝜃 на його оцінку . Превагу слід віддавати тим оцінкам, дисперсія яких невелика.
D
= – міра розкиду (кількісна)
– міра розкиду (кількісна)
Озн2:
Кількісною мірою похибки при заміні 𝜃
на
будемо
описувати величиною: μ (*)
(*)
μ
=
Очевидно,
що серед усіх оцінок з однаковою
дисперсією найменшу міру похибки буде
мати та для якої:
 =0 або
=0 або

Озн3:
Оцінка
називається незміщеною оцінкою параметра
 якщо
якщо
Озн4: Оцінка називається спроможною оцінкою для параметра , якщо
P{| |>
|> }=0,
∀ε
>
0, або
}=0,
∀ε
>
0, або
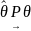
Якщо
→
з
ймовірністю «1» то
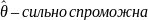 оцінка.
оцінка.
За
вказаною вибіркою { }
можна побудувати не оцінку а цілу
послідовність оцінок
}
можна побудувати не оцінку а цілу
послідовність оцінок
Озн5:
послідовність оцінок {
}
називається асимптотично незалежною
послідовністю оцінок, якщо μ (4)
(4)
Аналогічно виводиться поняття асимптотично спроможної послідовності оцінки.
Зауваж: Нехай { } – незміщена послідовність оцінка для параметра це означає:
Тоді
P{ }=P{|
}=P{| |>ε}≤
|>ε}≤
 ;
якщо
;
якщо
 0, то оцінка буде спроможною.
0, то оцінка буде спроможною.

 =
=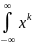 dF(x)
dF(x) = к-ий вибірковий момент =
= к-ий вибірковий момент =



 ;
; =
= ;
; =
= -
вибіркова
дисперсія
-
вибіркова
дисперсія