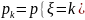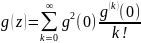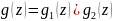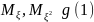1.Характеристичні функції, властивості.

При вивченні сум незалежних вв використовують характеристичні ф-ції:

Озн. Хар. ф-цією φ(z) вв ξ назив. комплексно-значна функція що визначається наступним співвідношенням: z є R φ(z)=Me^izξ=M(coszξ+isinzξ) (1).

Якщо відома ф-ція розп. F_ξ(x), то φ(z)=Me^izξ=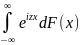 (Mg(ξ)= )

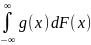а) ξ-абс-неп.,тобто мала щільність p(x) і φ(z)=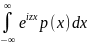

б) ξ-дискретна, p_k=P{ ξ =k}: φ(z)

-1	1
1/2	1/2

Пр. 1) ξ:

φ(z)=Me^izξ=1/2(e^-iz+e^iz)=cosz

2) ξ-має розподіл Пуассона

P{ ξ =k}=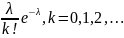 φ(z)= Me^izξ= =e^-λ =

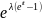
Властивості:

1) φ(0)=1; | φ(z)|<=1

2) φ(-z)= Me^i(-z)ξ=M(cosz ξ-isinz ξ)=

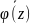
3) φ(z) – рівномірно-неперервна на числовій вісі

4) Якщо існують для вв ξ моменти порядку n M _ξⁿ <∞, то φ⁽ⁿ⁾ (0)=iⁿM_ξⁿ (2)

5) Харак. ф-ція однозначно визначає розподіл

Якщо у двох вв хар.ф-ції співпадають, то і результати співпадають.

6) Нехай ξ₁ і ξ₂ – незалежні вв, φ₁(z) і φ₂(z) – їх харак. ф-ції.

(ξ₁+ ξ₂): φ(z)= φ₁(z) φ₂(z)

Озн. G(x) – узагальнена ф-ція розподілу, якщо вона: 1)неспадна,2)неперервна зліва,3)

Озн. Кажуть що послідовність узагальнених ф-цій розп. {F_n(x)} збігається в основному до ф-ції розп. F(x) якщо точки неперервності цієї ф-ції MF_n(x)→F(x)

Т-ма(1 Хеллі)

послідовності ф-ції розподілу {F_n} збігається в основному до ф-ції розподілу F(x). Тоді непер. і обмеж. g(x): (*)

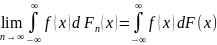Озн. якщо має місце (*) то кажуть що {F_n} прямує до F(x) слабко.

7) Нехай {F_n} слабко збігається до ф.р. F(x) тоді відповідна посл. хар. ф-цій φ_n(z)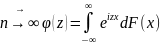 Якщо вв невід’ємна, то замість характеристичної ф-ції варто розглядати більш прості об’єкти з властивостями:

ξ- невід’ємна вв
Дискретна Твірна ф-ція 1) Твірна ф-ція однозначно визначає розподіл 2) ξ1 і ξ2 – незалежні, то 3)	невід’ємна перетв. Лапласа Ψ(s)=M 1) однозначно визначає розподіл 2) Ψ(S)= φ1(S) *φ2(S) 3) Ψ(n)(0)=(-1)n Ψ(S)= φ(-iz)

2. ЦГТ

При доведенні ЦГТ будуть необхідні наступні нерівності:

Лема. :

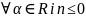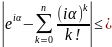(H1)

(H2)

З (H1)=> (H2)

До ЦГТ-м відносять твердження в яких мова йде про збіжність розподілу суми випадкових величин до нормального розподілу

Нехай ξ₁…ξ_n – незалежні вв.

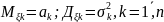– скінченні

ξ_k:F_k(x)=P{ξ_k˂x}

Познач. ξ₁+…+ξ_n)

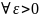
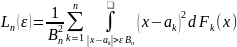
Якщо 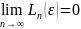(1), то викон. умова Ліндеберга.

Розкриємо зміст умови(1):

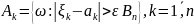
A={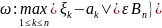

A=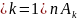

P(A)=P( )

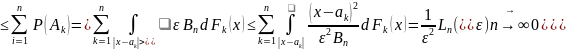
P(A)

Тобто, якщо викн. умова Ліндеберга значення вв ξ_k мало відрізняються від середніх – дуже малі

Ф_n(x)=P{S_n<x}. ф-ція розподілу вв. S_n

Ф_n(x)=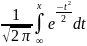 – ф-ція Лапласа ф.р.N(0,1)

3.Цгт для однаково розподілених випадкових величин

1. Якщо 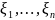незалежні однаково розподілені вв; тоді Доведення L(E)=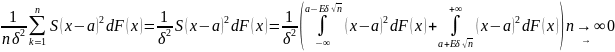

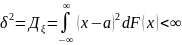
2. Інтегральна теорема Муавра-Лапласа

Нехай проводиться серія з n незалежних випробувань 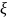- кількість успіхів. Тоді P(a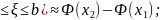

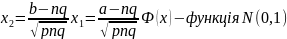
0	1
q	p

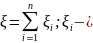Доведення кількість успіхів в іншому випробовуванні =

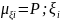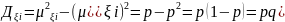За теоремою Лапласа: має N(0,1) є асимтетичною нормальною з пар.(0,1) P{a }=P{ a } P{ }=P{ }=Ф(x₂)-Ф(x₁)