25 Основні нерівності для математичного сподівання (Гельдера, Ієнсена, Ляпунова, Чебишева).
Нерівність Гельдера
Якщо
P>1,q>1,
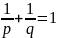Випадкові век. Ѯ I
n
такі, що
тоді
З
мал. Видно i
що b<
Очевидно що сума площ S
і T
буде нее менше ніж площа прямок. Зі
сторонами a
i
b.
Знайдемо
ab<=
Візьмемо
в якості a=
b=
Підставимо a
I
b
в (ab<=
)
і візьмемо мат. сподівання МС=>(1)
2.Нерівність Коші-буляковський
При
p=2,
q=2
в нерівності Гейдера одержемо
3.Нерівність Іенсона
Розглянемо
функцію q(x)
визначену на інтервалі I
g(x)-
опукла g(x)>=
g(
)k(
)(x-
)
Візьмемо:
x=
Ѯ:
=
Підставимо в g(x)>=
g(
)k(
)(x-
)
: g(Ѯ)>=
g(
)k(
)(
Ѯ -
3)М(g(Ѯ))>=g( )+0 М(g(Ѯ))>=g( )- для будь-якого опуклої , борелевої функції
4)
Нерівність Ляпунова 0<S<t
=>
<=
Нехай
r=
g(x)=
r>=1
Розглянемо n=
Для g(n)
випишемо нерівність Ієнсона: g(
<=
=
5)Нерівність
Чебишива для мат. сподівання Ѯ –
невід’ємне вв, a>0
P{
Ѯ >a}<=
Розглянемо
вв n=
n<=
Ѯ
26. Моменти, дисперсія, нерівність Чебишева для дисперсій. Розписати формули для моментів на випадок, якщо відома щільність випадкової величини .
Менш
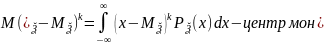
Дисперсія – це 2 центр момент
Властивості 1.
2.
3.
де
cov
(
)=
, якщо
4.
Нерівність Чебишива для дисперсії. Якщо
,
то для будь-якого Е>0 P{|
-
|>E}<=
P{|
-
|>E}=
P{
>
}<=
*
