21 Функція розподілу випадкової величини, властивості.

Озн1. Нехай (Ω,F,P) ймов. простір. дійсна ф-ія ξ= ξ(w) на Ω така , що для кожного дійсного х

{w : ξ(w)< x} є F,(1) наз. Випадковою величиною.

Озн.2 Ф-ія F(x) = P{ w : ξ(w)< x } xєR назив. функцією розподілу випадкової величини (ξ(w))

Зауваження!!! У функ. аналізі функція ξ= ξ(w) на Ω, для якої виконується (1) назив. вимірною відносно ᴑᴖ-алгебра F.

Властивості :

1.{w: = ξ(w)≥xy, {w= ξ(w))≤x}

2. {w: = ξ(w)>xy,{w:a≤ ξ(w)<b}

3. {w: = a< ξ(w)<by,{w: ξ(w)=x}

22.Теорема Колногорова

Нехай F(x) володіє такими властивостями:

1. F(x) – неперервна зліва; xє(-∞,∞)

2. F(x) – неспадна

3. Lim F(x)=1, Lim F(x)=0;

Тоді існує ймовірнисний простір (Ω,F,P) і випадкова велечина Ѯ(w) на ньому і функція розподілу якої =F(x)

Дов Ω(-∞,∞)

А клас усіх напіввідкритих інтервалів виду [а,b) і скінченних сум таких інтервалів

U_i=1[a_i,b_i), А-алгебра

НА множині цієї алгебри введем міру:

P{[a,b)}=F(b)- F(a)

P{ U_i=1[a_i,b_i)}=∑ⁿ_i=1(F(b_i)-F(a_i))

P(….)>=0, p(Ω)=P{(-∞,∞)}=1

P() скінченно-фдит. Ймовірнисна міра

P{ U_i=1[a_i,b_i)}=∑ⁿ_i=1(F(b_i)-F(a_i))

Розглянемо монотонно спадну послідовність множин {A_n}, A_n є А, A_n+1 є A_n першими таких множин є одразу і їхньою границею A_n = A є A. Покажимо що P(lim A_n)= lim P(A_n) A=[a.b), A_n=[a.b) Нехай A_n самий максимальний інтервал що містить [a.b) Поглинаючи здеякою n: A_n=[a.b)

Lim P(A_n)-Lim P{[a.b)}=LimF(b)-F(a) = F(b)-F(a)= P(A)->P() зліч. ад.йм.міра

₰-найменша δ алгебри що містить алгебру А. ₰=B(R) { Ω =(-∞,∞),₰=B(R);P()}

P{Ѯ<x}=P{(-∞,x)}=F(x)-F(-∞)=F(x)

23.Щільність випадкової величини. Властивості. Основні неперервні розподіли

Означення: Кажуть, що випадкові величин має щільність розподілу якщо існує інтегровна борелівська

функція P(x), така що для всіх х виконуюється F(x)= p(x) щільність

Якщо Р(х) – неперервна, тоді F(x) диференційований

P(x)=F^’ (x)

1)P(x)>=0 оскільки P(x)=F^’(х), а F(x) неспадна і F^’(х)>=0

2)P{a<=Ѯ<=b}=F(b)-F(a)=

3)

Основні неперервні розподіли

А) рівномірний розподіл на відрізку [a,b] Ѯ має , якщо її щільності

P_Ѯ(x)= F(x)= F(x)=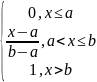 xє[a,b] F(x)= ^x_a=

Б) нормальний розподіл N(a , δ²)

Кажуть що В.В. Ѯ норм. Розподіл, якщо P(x)= в я явному вигляді F(x)не вдається знайти

F(x)= du

В)Експоненцільний розподіл з параметром λ

F_Ѯ(x)= ; P_Ѯ(x)=F^’(x)=

Г) Розподіл Коші

Ѯ= (x)= , xє( ) F(x)=

24 Означення математичного сподівання в загальному випадку. Властивості.

Ѯ абсолютно неп. Вв з щільністю P(x) тоді мат сподівання називається: = , якщо інтеграл в правій частині абсолютно збіжний ( ) Якщо відома функція в-в F(x) то можна дати загальне означення мат. Сподівання як для дискретного, так і для неперервного вигляду = Для дискретного в.в. = У випадку коли кількість w нескінченна, ця функція набуде вигляду . = – інтеграл Лебеча

Нагадаємо властивості мат. Сподівання

1) 2) 3)

4) g(x) – борелева функція

5) Якщо Ѯ I n М залежні в.в.

6) Ѯ>=0 :

7) Ѯ>=n => >=