13. Пуассоновий розподіл як апроксимація біноміального, формула Пуасоона, геометричний розподіл.

- незалежна випр. Бернулі

– к-сть успіхів в серії з n випробувань

Pn(K) = де n  , p0, np= (0, )

= = =

= = = 

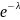
Pn(k) –Формула Пуасона ;

Випадкова величина , яка мае розподіл P = , k=0,1,2…..- Пуасонова випадкова величина.

14. Локальна та інтегральна теореми Муавра-Лапласа.

Т-ма(локальна) Якщо імовірність написання події А в кожному з n незалежних випробувань однакова і дорівнює р, то рівномірно по к, для яких Х = знаходиться в сталих межах (- <a ) має місце співвідношення 1 , де

= - лок формула Лапласа

Т-ма(інтегральна) Нехай – к-сть появ події А в серії з n незав випробувань

{a b}=Ф(b) – Ф(q), де Ф(х) = du

На практиці : Pn(x1 , a= ; b=

15.Математичне сподівання дискретної випадкової величини, властивості. Дисперсія, властивості.

Нехай дискретна випадкова величина може приймати rрізних значень: X1…Xr n разів провели експеримент і фіксували значення випадкової величини : а1,…,аn Середне значення спост величин:

= К-сть появ подій { _{=Xi} =} Озн. Якщо –дискретна випадкова величина яка набувае значень Х1,Х2,…,Хn , P1,…,Pn… тоді ії мат сподівання називають величину М =

Власт.

1. 

Дов. Нехай Hi = {Wi: (W)=Xi}

H1 H2 = , Hi∩Hj =

{Hn}- Повна група подій

= = =

2. 

Дов M( )=

3. Mc=C, C-Стала

Дов. Mc=

4. =C , C- Стала

Дов.

5. Якжо

Дов.

6. Якщо

Дов.

0= V

P{

7. Нехай g(x) – числова ф-ція

– диск вип. вел. = D( )

Дов.

16. Сумісний розподіл двох дискретних випадкових величин.

Дві випадкові величини якщо для будь якого числових множин А та В події є А} { єВ} – незалежні тобто:

Т-ма1 Нехай х1,х2… - значення випадкової величини Р{ =Xi}= pi

y1,y2… знач. в.в. P{ =yj}=pj

Для незалежності в.в. необхідно і досить щоб події { }та{ }були незалежними для будь якого xi,yj, дов.

P{ } = = = =

Т-ма2 Якщо f(x) i g(x) – для будь якої монотонноі функції незалежні вип. величини тоді в.в f( ) та g( теж незалежні

18 . Коефіцієнт кореляції, властивості.

Для будь-якого | |<=1. Якщо то між Розглянимо : n1=

- = =

Cov( )=M = = Одже якщо якщо Нехай пов’язані ліпістною залежністю: n= cov( )= =

Нехай для вв =>

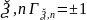
= n=

19. Умовний розподіл двв і умовне математичне сподівання

P(x_i,y_j) = P{ξ= x_i, η= y_j}, i=1,n j=1,m – сумісний розподіл

P_{η /ξ} { y_j / x_i } ≡ P{η=y_j / ξ = x_i} = = – умовний розподіл в. в. η (при умові що ξ=х_і)

М(η / ξ=x_i) = P_{η /ξ} {y_j / x_i} = = (9) – умовне мат сподівання η (УМС) при умові ξ=х_і

М(η / ξ=х_і) ≈ M(η / x_i)

Очевидно що (9) може розглядатися як функція від х М(η / x) – функція від х – регресія, а її графік – крива регресії. З іншого боку при різних х_і мат сподівання М(η /x_i) буде числом, тобто в залежності від випадку у МС набуває різних значень.

Озн: М(η / x_i) називається умовним мат сподіванням η при заданому ξ.

М(М(η / ξ)) = P{ξ= } =

формула повного мат сподівання

= = = M_η

Зауваження: Якщо ξ, η незалежні, М(η / ξ=x)=M_η