9) Умовні ймовірності, властивості. Формула множення.

В ряді випадків доводиться розглядати ймовірність подій якщо відомо, що деяка подія В відбулася

Озн. Нехай (Ω, F, P) – ймовірнісний простір. Нехай P(B) > 0. Тоді умовною ймовірністю подій А, за умови що В – відбулася називають ймовірність:

P(A \ B) = (1)

1. ∀ A ∈ F : P(A / B) ≥ 0

2. P(Ω / B) = 1

3. P(B / B) = 1

4. {A_i} – попарно несумісні події. Тоді

P( ) =

P( ) = = = =

Зауваження: позначимо через F_B σ – алгебру усіх множин А / В, ∀ А ∈ F . тоді з властивості 1-4 => що (В, F_B P(./B)) може вважатися ймовірнісним простором.

Твердження Якщо P(B) > 0; P(A) > 0, то Р(А ∩ В) = Р(А / В) ۰Р(В) = Р(В / А) ۰ Р(А) (2)

(2) – теорема множення.

Формула (2) допускає узагальнення:

Якщо А_1­,…,А_n – випадкові події:

P(A₁ ∩…∩ A_n-1) > 0

Оскільки c c…c A₂ ∩ A₁ c A₁,…

P(A_n\ ) – визначені, е = 1,n має місце рівність

P( ) = P(A₁) P(A₂ / A₁) + P(A₃/ A₂ ∩ A₁) = P(A_n / A₁ ∩ A₂ ∩…∩ A_n-1)

10) Повна група подій. Формула повної ймовірності. Формула Байєса

Озн: Послідовність випадкових подій Н₁,…,Н­_n утворює нову групу подій, якщо:

1. Об’єднання Н₁∪,…,∪Н_n (4)

2. Н_і ∩ H_j = ∅, i≠j (5)

Теорема Якщо Н₁,…,Н_n – повна група подій, і Р(Н_і) > 0 i=1,n тоді для ∀ А ∈ F має місце рівність:

P(A) = P(H_i) – формула повної ймовірності

А=А ∩ Ω = А ∩ (Н₁∪…∪ Н_n­) = (А ∩ Н₁) ∪…∪(А∩Н_n)

P(A) = = P(H_i)

Теорема Якщо Н₁,…, Н_n – ПГП і Р(Н_і) > 0, і=1.n, тоді для ∀ А ∈ F, для якої Р(А) > 0 має місце рівність Р(Н_і | A) = 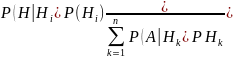– формули Байєса

P(H_i | A) = = , і=1,n

11. Незалежні випадкові події. Властивості незалежних подій.

Нехай (Ω,F,P) – ймовірнісний простір випадкової події A,B € F називаеться незалежними, якщо P(A∩B) = P(A) P(B).

Властивості:

Т-ма(1) Нехай P(B)>0, Тоді події A I B незалежні  коли P(A\B)=P(A)

дов. Нехай АіВ незалежні тоді P(A|B)= = =P(H)

<=) P(A\B)=P(A)  =P(A)  P(A∩B) = P(A)P(B)

Т-ма(2) Якщо події А і В незалежн, то незалежними будуть і такі події і A i , i .

дов. P(A∩ ) =? P (A) * P ( )

розг. A∩ =A\(A∩B) , P(A∩ )=P(A)-P(A∩B) = P(A) – P(A)*P(B)= P(A)*(1-P(B)) =P(A)* P( )

Т-ма(2) Якщо події А і В1- незалежні, А і В2 – незалежні, а В1 і В2 – несумісні В1∩В2 тоді А і В1 B2 –незалежні

дов. P(A∩(B1 B2)) = P((A∩B1) (A∩B2)) =P(A∩B1) + P(A∩B2) = P(A) P(B1) + P(A) * P(B2) = P(A) (P(B1) + P(B2)) = P(A) P(B1 B2)

Озн. – послідовність подій. Випадкові події А1…Аn наз. Незалежними в сукупності, якщо для будь якого К і набору індексів і1 і2 … ік виконуеться

P( ) = ).

12. Дискретна випадкова величина, розподіл двв. Біноміальний розподіл, формула Бернуллі.

Озн1. Випадкові величини на дискретному ймовірнісному просторі назив. Дискретна функція що діє із множини Ω в множину R.

Озн2. Дискретною випадковою величиною – приймає лише скінчену чи змічену к-ть значень.

Біноміальний розподіл:

Озн. Схемою випробувань Бернулі наз. Серія з n незалежних випробувань, причому в кожному з яких може бути лише два результати:

«успіх» з імовірністю Р , і «неуспіх» з імовірністю q = 1-p

– к-сть успіхів в серії з n випробувань Бернулі

Результатом експериметра, при якому ми можем сказати що відбулася саме к успіхів, можна важати як набір із n букв в якому саме к був «у» і «n-k» букв. «Н» ймовірність настання такого результату це .

P = , k = 0,1,2… n – фрм. Бінарного розподілу

Pn(K) = – Формула Бернулі