1. Стохастичний експ. – результат якого передбачити неможливо. Не з всіх стохастичних експ. можна побудувати адекватну математичну модель. Стох. Експеремент має задоволняти такі властивості:

1) масовість – експеремент можна повторювати велику кількість разів.

2)результати попердніх проведень експ. не повинні впливати на результат наступних експериментів – незалежність

Приклади:

1) СЕ {підкидання грального кубика}

2) СЕ {підкидання двох монет}

3) СЕ {підкидання монети до першої появи герба}

Ω - простір елементарних подій , а точки цього простору (w) взаємовиключеними ( всеможливі) результатами експерименту.

СE описують за допомогою Ω в рамках теоретико – множинного моделювання теорії ймов.

Приклади:

1) Ω = {1,2,3,4,5,6} - скінченний

2) Ω = {ГГ, ГЦ, ЦГ, ЦЦ} - скінченний

3) Ω={Г, ЦГ, ЦЦГ, … , Ц..ЦГ} – злічений

4) CE {спостереження за рухом мікроскопічної частинки в рідині} Ω - {всеможливі траєкторії руху частинки} – нескінченний простір

Випадкова подія

1.Нехай А – будь-яка випадкова подія, що розглядається в стохастичному експеременті. Оскільки кожна елементарна подія (кожен результ експ.) w дає повну інформацію про результат експ. описується точкою w є Ω одразу можна сказати відбулася чи не відбулася подія А, тобто, по відношенню до кожної події, простір Ω можна розбити на 2 множини: А´ і А´´, які є А´∪ А´´= Ω А´∩ А´ = Ø. В А´ знаходяться ті результати експерименту, при яких подія А відбулася. А´ - множина сприятливих подій.

Приклади:

1) Ω = {1,2,3,4,5,6} А- {випаде число 3} А - {3,6}

2) Ω = {ГГ, ГЦ, ЦГ, ЦЦ} A{хоть один раз випав Г} А-{ГГ,ГЦ,ЦГ}

3) підкидаємо монету до першої появи герба. А {герб випаде при 3-тьому підкиданні} А-{ЦЦГ} А{треба зробити не більше 3-ох підкидань до появи герба} А-{Г,ЦГ,ЦЦГ}

Дії над подіями:

1. Множина Ω може сприйматися як подія що відбувається завжди, тобто достовірна подія.

2.Підмножиною Ʉ множини Ω є порожня множина. Порожню множину можна ототожнювати з подіями, які ніколи не відбуваються в рамках експеременту. (неможлива подія)

3.А с B - подія А викликає появу події B

А с Ω, Ø с А – по домовленості

4. А ∪ В. А +В – подія яка відбувається, тоді і лише тоді, коли відбувається або подія А, або В.

А ∩ Ø = А , А ∪ Ω = Ω, А с А ∪ В, В с А ∪ В, А с С, В с С звідци слідує А ∪ В с С – об*єднання двох подій можна розглядати , як точну верхню грань подій А і В.

5. А ∩ В – подія, яка відбувається тоді ілише тоді, коли відбувається і А і В. Дві події називаються несумісними , якщо є їх добуток є неможливою подією А ∩ В = Ø.

6. А(заперечене) = Ω\А , А с Ω. А(заперечене) протилежна подія до події А, відбувається лише тоді коли А не відбувається.

7. А\В – подія, яка відбулася лише тоді, коли відбулася подія А і не відбулася В. А(заперечене)= Ω\А А\В=А∩ В(заперечене)

2. Частота випадкової події.

Маємо СЕ і А- спостерігається в даному СЕ потворимо експ. n разів і Kn(А) – кількість появ події А в серії СЕ-ів.

Озн1. Відношення Vn(А) =Kn(A)/n називається частотою А в проведеній серія експериментів.

Властивості частоти:

1) 0 ≤ Vn(A)≤1 – чатсота приймає знач від 0 до 1 бо 0≤Kn(A)≤n

2) частота появи достов. події: Vn (Ω)=1, Kn(Ω)=n.

3) А ∩ В = Ø (А і В - несумісні), то Vn(А ∪ В)=Vn(A)+Vn(B), Kn(А ∪ В)=Kn(A)+Kn(B)

При достатньо великих n для більшості серій експериментів частота зберігає майже стале значення , причому відхилене від цього значення тим рідше чим більше n

Якщо при великих n частота появи події А (Vn(A)) мало відрізн. Від деякого числа Р, то подія А назив. «стохастичною», а р-ймовірність події А. Наведене означення є емпіричним (шляхом досвіду одержання)

Основні задачі теорії ймовірності:

1. Формалізація поняття ймовірності, вивчення об*єктів в яких введене це поняття.

2. Створення і вивченя ймовірностних моделей реальних явищ.

3. Розробка методів перевірки адекватності запропонованих ймовірностних моделей.

3.Йморвірнісна модель се із скінченною чи змінною кількістю можливих результатів.

СЕ⩪ Ω = {W1,….,Wn,….} – дискретний простір елем.

Припустимо що кожній елементарній події Wi можна приписати «вагу» Pi, причому так що:

1)Рі≥0 2)   Рі=1

Pi –ймоввірність елементарної події Wi Нехай А будь-яка подія, що спостерігається в даному СЕ. Озн2. Ймовірність події А назвемо суму ймовірності елементів подій, які сприяють появі події А.

4. Алгебра і сигма-алгебра подій, скінчено-адитивна імовірнісна міра, зліченно-адитивна імовірнісна міра, теорема про продовження міри.

Озн1. Клас R підмножин Ω називається алгеброю, якщо:

1) Ω є R

2)А є R «звідси слідує» 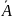є R

3)A є R і B є R А ∪ В є R ,

Озн2. Клас F множин з Ω назив. ᴑᴖ -алгеброю, якщо:

1) Ω є R

2) А є R є R

3) Якщо Аі є F, і=1,2… , то Ai є F.

Озн3. Нехай К – деякий клас підмножин з Ω, ᴑᴖ(K) –найменша ᴑᴖ-алгебра, що містить клас К, якщо:

1)К с ᴑᴖ(К)

2) інших ᴑᴖ-алгебр F , що містить лямбда ᴑᴖ(К) с F.

Твердж. класу множин К існує ᴑᴖ(К).

Озн4. Функція Р() назив. скінченно – адитивною мірою на алгебрі R, якщо :

1)Р(А) ≥0, А є R

2) P(Ω)=1

3)P( )=P(A)+P(B); = Ø, A,B є R

Озн5.

Ф-ція множин Р() назив. зліченно-адитивна ймовірністкою мірою на алгебрі R, якщо:

1) Р(А) ≥0, А є R

2) P(Ω)=1

3)P ( Аі) = ; Аі Аj = Ø, i j

Теорема про продовження міри

Нехай Р() – злічена адитивна ймовірність міра на алгебрі R. Тоді існує злічено адитивна ймовірність міра Q() на ᴑᴖ(R) така що: Q(A) =P(A), для будь якого A є R

5. -алгебр борелевих множин в , -алгебр борелевих множин в , борелева функція .

Озн. Нехай f(x) – функція на n – вимірному просторі із значеннями в R, B( ) - ᴑᴖ-алгебра кореневих множин тобто найменша ᴑᴖ-алгебра, що містить усі «піввідкриті» паралелепіпиди виду ( ) . Ф-ція f(x):R´´ R, вимірна відносно ᴑᴖ-алгебра B (R´´) наз. Берелевською функцією.

Всі неперервні ф-ції є борелевськими

f(x):R´´ R, С є R {x: f(x) є С} є B (R´´)