4.Технология решения в Excel.

4.1 Ввод в Exсel.

После построения математической модели, необходимо перенести её в ЭТ Excel. Этот процесс, как для данного контрольного примера, так и для всех последующих решаемых задач оптимизации, может быть реализован в виде последовательности следующих этапов.

• Продумайте организацию исходных данных модели и введите их (коэффициенты целевой функции и ограничения) в ЭТ, снабдив понятными названиями.

• Зарезервируйте n отдельных ячеек для независимых переменных математической модели.

• В одной из ячеек создайте формулу, определяющую целевую функцию.

• Выберите ячейки и создайте в них формулы, соответствующие правым частям ограничений.

• Запустите программу Поиск решения для решения задачи.

• Проанализируйте полученное решение и отчеты, и определите возможные пути улучшения решения за счет снятия каких-либо ограничений.

Вначале подготовим электронную таблицу (лист) Excel для применения данной надстройки “Поиск решения”.

Введем значения коэффициентов целевой функции: ячейки B3:G3 на рисунке 1.

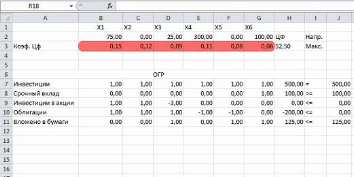
Рисунок 1

В ячейках B2:E2 показан результат решения.

В ячейках H7:H11, J7 и J11 введем формулы ограничений соответственно:

=СУММПРОИЗВ(B2:G2;B7:G7)

=СУММПРОИЗВ(B8:G8;B2:G2)

=СУММПРОИЗВ(B9:G9;B2:G2)

=СУММПРОИЗВ(B10:G10;B2:G2)

=СУММПРОИЗВ(B11:G11;B2:G2)

В ячейку G4 запишем формулу целевой функции:

=СУММПРОИЗВ(B2:G2;B3:G3)

4.2Поиск решения.

Откроем диалоговое окно «Поиск решения». В нем зададим расположение целевой ячейки (в котором вычисляется значение целевой функции), вид оптимального решения (максимальное значение), расположение ячеек, которые будут изменяться при поиске решения (из них состоит вектор-строка оптимального плана), а также ограничения на изменяемые значения.(Рис.2).

После ввода необходимых данных нажмем кнопку «Выполнить» диалогового окна. В случае, если решение существует (и все данные введены верно), появляется сообщение как на рисунке 3.

Рисунок 2

Рисунок 3

После нажатия кнопки «Найти решение» в ячейках строки оптимального плана появляются значения его оптимальных элементов (оптимальный план); в ячейке целевой функции вычисляется соответствующее этому плану оптимальное значение целевой функции.(рис.4). На рисунке видно, что в оптимальном решении :

-Объем использования рекламы на телевидении равен 2.(B2)

-Объем использования радиорекламы в месяц равен 8.(C2)

-Реклама в газете “Биржа”-517 кв. см.(D2)

-Реклама в газете “Рекламный вестник” равен 0.(E2)

При этом максимальная прибыль будет составлять 24167 руб.(G4)

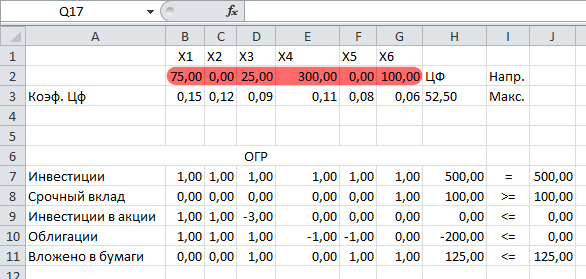
Рисунок 4

4.3 Анализ отчетов.

4.3.1.Отчет “Результаты”.

В первой таблице (Рис.5) приведено исходное (до начала вычислений) и окончательное (оптимальное) значение ячейки, в которой записана целевая функция задачи.

Во второй таблице представлены значения искомых оптимизируемых переменных, исходные и полученные в результате решения задачи.

Последняя таблица содержит результаты оптимального решения для ограничений и граничных условий. В графе Значение приведены рассчитанные оптимальные значения потребных ресурсов и оптимизируемых переменных.

В графе Формула приведены зависимости, которые были введены в диалоговое окно Поиск решения.

Графа Статус определяет связанными или несвязанными являются те или иные ограничения. Под «связанными» здесь понимаются ограничения, которые реализуются в оптимальном решении в виде жестких равенств.

Рисунок 5

В данном случае Время теле- , радио- рекламы является связанным ограничением. Т.к. теле-радиореклама занимает 10 минут. Так же и бюджет расходуется весь и является связанным.

Последняя графа Разница определяет неиспользуемый остаток несвязанного ресурса, т.е. разность между потребным количеством ресурсов и их наличием.