30/ Аддитивная и мультипликативные модели временного ряда.

Рассмотрим модели ВР, в которых уровни представляются в виде суммы или произведения следующих 4х компонент: T(t) - тенденция, S(t) – сезонная составляющая, C(t) – циклическая составляющая, ε(t) – случайная составляющая.

Тогда: y_t=T(t)+S(t)+C(t)+ε(t) – аддитивная модель;

y_t=T(t)*S(t)*C(t)*ε(t) – мультипликативная модель.

Выбор  одной  из  трех  моделей  осуществляется  на  основе  анализа структуры  сезонных  колебаний. 

Если  амплитуда  колебаний  приблизительно постоянна,  строят аддитивную  модель  временного  ряда,  в  которой  значения сезонной  компоненты  предполагаются  постоянными  для  различных  циклов.

Если  амплитуда  сезонных  колебаний  возрастает  или  уменьшается,  строят мультипликативную  модель  временного  ряда,  которая  ставит  уровни  ряда  в зависимость от значений сезонной компоненты. 

31/ Явления автокорреляции и авторегрессии временного ряда.

Автокорреляция – это явление, при котором случайные ошибки разных наблюдений коррелированны, т.е. cov(ε_i;ε_j)≠0.

Как правило, если автокорреляция присутствует, то наибольшее влияние на последующее наблюдение оказывает результат предыдущего наблюдения. Это явление называется авторегрессией, т.е. когда значения временного ряда в данный момент линейно зависят от предыдущих значений этого же ряда. 

Количественно ее можно измерить

с помощью линейного ко­эффициента корреляции между уровнями исходного

временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во

времени. Коэффициент корреляции имеет вид:

можно определить коэффициенты автокорреля­ции второго и более высоких порядков.

Так, коэффициент авто­корреляции второго порядка характеризует тесноту связи

между уровнями у_t и y_t-1 и

определяется по формуле:

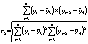
Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорре­ляции, уменьшается.

Отметим два важных свойства коэффициента автокорреляции. Во-первых, он строится по аналогии с линейным коэффициентом корреляции и таким образом характеризует тесноту только линейной связи текущего и предыдущего уровней ряда. Во-вторых, по знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уров­нях ряда.

Последовательность коэффициентов автокорреляции уров­ней первого, второго и т.д. порядков называют автокорреляцион­ной функцией временного ряда. График зависимости ее значений от величины лага на­зывается коррелограммой.

Причины:

Чаще всего наблюдается, когда эконометрическая модель строится на основе временных рядов. Если существует корреляция между последовательными значениями некоторой независимой переменной, то будет наблюдаться и корреляция последовательных значений остатков. А. мб также следствием ошибочной спецификации эконометрической модели. Наличие А. может означать, что необходимо ввести в модель новую независимую переменную.

Последствия:

А. приводит к снижению качества МНК-оценок параметров, к увеличению тестовых статистик, по которым определяется качество модели (т.е. создается искусственное улучшение качества модели относительно ее действительного уровня точности).

Оценки неизвестных коэффициентов нормальной регрессионной модели являются несмещенными и состоятельными, но при этом теряют свойство эффективности

Растет вероятность того, что оценки стандартных ошибок коэффициентов модели будут рассчитаны неверно, что может привести к утверждению неверной гипотезы о значимости коэффициентов и значимости модели.

Способы обнаружения:

1) Тест Дарбина-Уотсона.

Определяет наличие А. между соседними членами. Используется статистика DW:

Границы:

2. Тест серий

Если имеется корреляция между соседними наблюдениями, то естественно ожидать, что в уравнении et=ρe_t-1+ν_t, t=1…n (авторегрессионное уравнение первого порядка) коэффициент ρ окажется значимо отличающимся от нуля. Плюсы метода в том, что обнаруживается корреляция не только между соседними, но и более отдаленными наблюдениями, и в том, что в отличие от теста Дарбина, нет областей неопределенности.

3)Q-тест Льюинга-Бокса

Рассмотрение выборочных автокорреляционной r(τ) и частной автокорреляционной r_част(τ) функций временного ряда.

Если ряд стационарный, то выборочный частный коэффициент корреляции совпадает с оценкой обычного МНК коэффициента ß_рв авторегрессионной модели AR(p):

yt=ß₀+ß₁y_t-1+…+ß_py_t-p+ε_t

Это утверждение лежит в основе вычисления значений частной автокорреляционной функции.

Коррелограмма - это график выборочной автокорреляционной функции. Это быстро убывающая функция. В случае отсутствия автокорреляции все значения автокорреляционной функции равны нулю. Отличие выборочного значения r(τ) не должно быть существенным.

Ослабление влияния:

• подбор соответствующей модели – авторегрессионнойAR(p), скользящей средней MA(q) или авторегрессионной модели скользящей средней ARMA(p,q) для случайных возмущений регрессии. Предполагается, что ошибки регрессии образуют стационарный временной ряд.

• метод элементарного подбора. Если все значения выборочной частной автокорреляционной функции порядка выше p незначимо отличаются от нуля, ВР следует идентифицировать с помощью модели, порядок авторегрессии которой не выше p.

• модель скользящей средней*: y_t=ε_t+γ₁ε_t-1+γ₂ε_t-2+…+γ_qε_t-q; если значения выборочной автокорреляционной функции порядка выше q незначимо отличаются от нуля, временной ряд следует идентифицировать с помощью модели скользящей средней, порядок которой не выше q.

*Метод скользящих средних основан на переходе от начальных значений членов ряда к их средним значениям на интервале времени, длина которого определена заранее. При этом сам выбранный интервал времени «скользит» вдоль ряда.