Тест ранговой корреляции Спирмена

Значения xi и ei ранжируются (упорядочиваются по величинам). Затем определяется коэффициент ранговой корреляции:

где di — разность между рангами xi и ei, i = 1,..., n ; 6 — число шесть (иногда думают, что это стандартное оклонение).

Доказано, что если коэффициент корреляции ρ_x,|e| для генеральной совокупности равен нулю, то статистика:

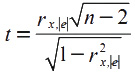
имеет t-распределение Стьюдента с числом степеней свободы v = n - 2.

Следовательно, если наблюдаемое значение t-статистики, вычисленное по формуле представленной выше, превышает t_кр = t_α/2,n-2 (определяется по таблице критических значений распределения Стьюдента), то нужно отклонить гипотезу о равенстве нулю коэффициента корреляции ρ_x,e, следовательно, и об отсутствии гетероскедастичности. В противном случае гипотеза об отсутствии гетероскедастичности принимается.

Устранение гетероскедастичности

Метод взвешенных наименьших квадратов. Наиболее простым методом устранения гетероскедастичности остатков модели регрессии является взвешивание параметров модели регрессии. В этом случае отдельным наблюдениям независимой переменой, характеризующимся максимальным среднеквадратическим отклонением случайной ошибки, придаётся больший вес, а остальным наблюдениям с минимальным среднеквадратическим отклонением случайной ошибки придаётся меньший вес. После данной процедуры свойство эффективности оценок неизвестных коэффициентов модели регрессии сохраняется.

25. Числовые характеристики модели множественной линейной регрессии

Множественная регрессия представляет собой регрессию результативного

признака с двумя и большим числом факторов, т. е. модель вида .

1.Частные коэффициенты эластичности. Внимание отдельных факторов в многофакторных моделях может быть охарактеризовано с помощью частных коэффициентов эластичности, которые в случае двухфакторной модели вычисляются по формулам:

Частные коэффициенты эластичности показывают, на сколько процентов измениться результирующий признак, если значение одного из факторных признаков измениться на 1%, а значение другого факторного признака останется не низменным.

2.Бета-коэффициент показывает, на какую часть величины средне­го квадратического отклонения S_y изменится зависи­мая переменная Y с изменением соответствующей независимой пере­менной Х_j на величину своего среднеквадратического отклонения при фиксирован­ном на постоянном уровне значении остальных независимых пере­менных.

Указанные коэффициенты позволяют упорядочить факторы по степени влияния факторов на зависимую переменную.

3.Коэффициент множественной корреляции (R) характеризует тесноту связи между результативным показателем и набором фактор­ных показателей:

где σ² — общая дисперсия эмпирического ряда, характеризующая общую вариацию результативного показателя (у) за счет факторов;

σ_ост² — остаточная дисперсия в ряду у, отражающая влияния всех факто­ров, кроме х;

Коэффициент множественной корреляции принимает только поло­жительные значения в пределах от 0 до 1. Чем ближе значение коэффи­циента к 1, тем больше теснота связи. И, наоборот, чем ближе к 0, тем за­висимость меньше. При значении R < 0,3 говорят о малой зависимости между величинами. При значении 0,3 < R < 0,6 говорят о средней тесноте связи. При R > 0,6 говорят о наличии существенной связи.

Квадрат коэффициента множественной корреляции называется коэффициентом детерминации (D): D = R². Коэффициент детермина­ции показывает, какая доля вариации результативного показателя свя­зана с вариацией факторных показателей.

4. Коэффициент множ-ой детерминации (R2) - показывает какая доля вариации (дисперсии) признака (рез.переменой) У учтена в модели множ-ой регрессии и обусловлена влиянием об. переменных, включенных в модель. =1 – =

5. Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и рассчитывается по формуле:где n-число наблюдений; m – число факторов. .

Недостаток нескорректированного коэффициента детерминации в том, что R2 увеличивается при введении новых факторов, хотя качество уравнения регрессии может и не возрастать, т.е. вводимые регрессоры являются малозначимыми. Скорректированный(адаптивный) коэффициент множественной детерминации определяется по формуле:

6. Дельта–коэффициент показывает долю влияния каждого фактора в суммарном влиянии всех факторов на зависимую переменнуюY.