Вопрос 17 Модели регрессии, нелинейные по факторным переменным
К моделям регрессии, нелинейным относительно включённых в анализ независимых переменных (но линейных по оцениваемым параметрам), относятся полиномы выше второго порядка и гиперболическая функция.
Модели регрессии, нелинейным относительно включённых в анализ независимых переменных, характеризуются тем, что зависимая переменная yi линейно связана с параметрами β0…βn модели.
Полиномы или полиномиальные функции применяются при анализе процессов с монотонным развитием и отсутствием пределов роста. Данному условию отвечают большинство экономических показателей (например, натуральные показатели промышленного производства). Полиномиальные функции характеризуются отсутствием явной зависимости приростов факторных переменных от значений результативной переменной yi.
Общий вид полинома n-го порядка (n-ой степени):
Чаще всего в эконометрическом моделировании применяется полином второго порядка (параболическая функция), характеризующий равноускоренное развитие процесса (равноускоренный рост или снижение уровней).:
Полиномы, чей порядок выше четвёртого, в эконометрических исследованиях обычно не применяются, потому что они не способны точно отразить существующую зависимость между результативной и факторными переменными.
Гиперболическая функция характеризует нелинейную зависимость между результативной переменной yi и факторной переменной xi, однако, данная функция является линейной по оцениваемым параметрам β0 и β1.
Гиперболоид или гиперболическая функция имеет вид:
Данная гиперболическая функция является равносторонней.
В качестве примера эконометрической модели в виде гиперболической функции можно привести модель зависимости затрат на единицу продукции от объёма производства.
Модели регрессии, нелинейные по оцениваемым коэффициентам
Нелинейными по оцениваемым параметрам моделями регрессииназываются модели, в которых результативная переменная yi нелинейно зависит от коэффициентов модели β0…βn.
К моделям регрессии, нелинейными по оцениваемым параметрам, относятся:
1) степенная функция:
2) показательная или экспоненциальная функция:
3) логарифмическая парабола:
4) экспоненциальная функция:
5) обратная функция:
и т.д.
Модели регрессии, нелинейные по оцениваемым коэффициентам, делятся на два класса:
1) модели регрессии, которые можно с помощью преобразований привести к линейному виду;
2) модели регрессии, которые невозможно привести к линейному виду.
Для оценки неизвестных параметров моделей регрессии, которые нельзя привести к линейному виду, нельзя применять классический метод наименьших квадратов. В этом случае используются итеративные процедуры оценивания (квази-ньютоновский метод, симплекс-метод, метод Хука-Дживса, метод Розенброка и др.).
18. Задача множественного корреляционно – регрессионного анализа. Спецификация эконометрической модели множественной регрессии. Условия Гаусса – Маркова для модели множественной регрессии.
Экономические явления, как правило, определяются большим числом одновременно и совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимости одной зависимой переменной У от нескольких объясняющих переменных Х1, Х2,…..Хn. Эта задача решается с помощью множественного регрессионного анализа.
У=F(Х1, X2, ….. Xk)+E
Обозначим i-e наблюдение зависимой переменной уi, а объясняющих переменных – xi1, xi2, … xik. Тогда модель множественной линейной регрессии можно представить в виде:
Y=b0+b1X1+b2X2+……+bkXk+E
Предпосылки для множественного регрессионного анализа могут быть записаны следующим образом:
В матричной форме модели Y=Xb+E, E-случайный вектор, Х- неслучайная (детерминированная) матрица
M(E)=0
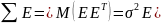
E-нормально распределенный случайный вектор, то есть Е
N(0;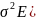
r(X)=p+1
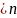
Модель, удовлетворяющая приведенным предпосылкам, называется классической нормальной линейной моделью множественной регрессии.
Теорема
Гаусса – Маркова, рассмотренная для
парной регрессионной модели, оказывается
верной и в общем виде для модели
множественной регрессии: при выполнении
предпосылок (кроме предпосылки о
нормальном распределении) множественного
регрессионного анализа оценка МНК b=(
является наиболее эффективной, то есть
обладает наименьшей дисперсией в классе
линейных несмещенных оценок.