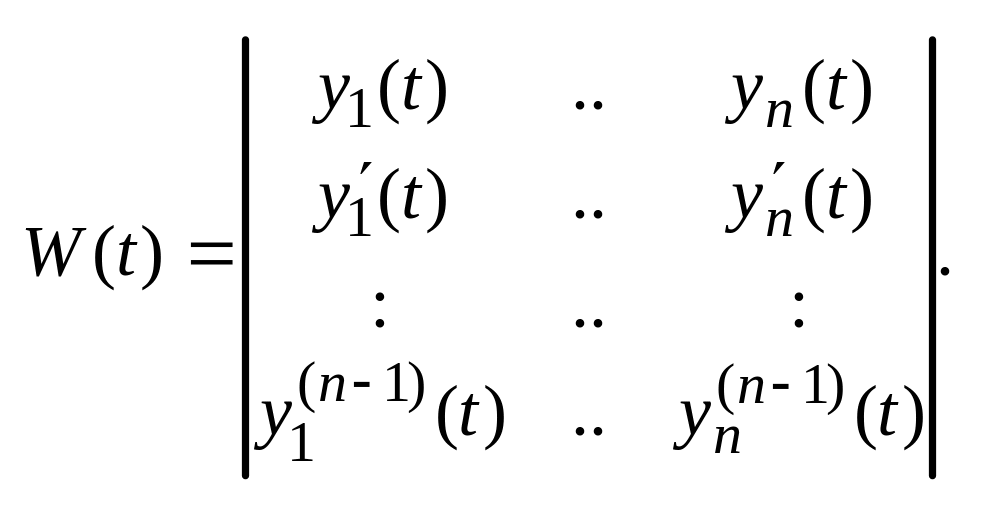- •Алгебра и геометрия
- •I.1. Матрицы и операции над ними. Обратная матрица.
- •I.2. Линейные преобразования и их матрицы. Собственные значения и собственные векторы.
- •I.3. Основная теорема алгебры и её следствия.
- •I.4. Векторы, операции над ними (сложение, умножение на число, скалярное, векторное и смешанное произведения), коллинеарность и компланарность векторов.
- •I.5. Линейная зависимость системы векторов.
- •I.6. Взаимное расположение прямых и плоскостей в пространстве.
- •II.1. Формула нахождения обратной матрицы.
- •II.2. Критерий совместности системы линейных уравнений.
- •II.3. Соотношения между размерностями ядра и образа линейного оператора в конечномерном пространстве.
- •II.4. Экстремальное свойство проекции вектора на линейное подпространство.
- •I.1. Определение множества. Операции над множествами. Равенство множеств. Включение, строгое включение. Свойства.
- •I.2. Отношения, декартово произведение, отношение эквивалентности. Операции над отношениями. Способы задания отношений.
- •I.3. Рекуррентные последовательности. Последовательность чисел Фибоначчи.
- •I.4. Булевы функции от двух переменных. Способы задания булевых функций.
- •I.5. Основные замкнутые классы во множестве булевых функций.
- •II.1. Биномиальная формула:
- •II.2. Перестановки, размещения и сочетания с повторениями.
- •II.3. Перестановки, размещения и сочетания без повторений.
- •II.4. Рекуррентные соотношения. Решение линейных рекуррентных соотношений второго порядка.
- •II.5. Эйлеровы графы. Критерий эйлеровости графов.
- •I.1. Постановка задачи Коши для оду n-го порядка. Достаточные условия разрешимости
- •I.2. Линейные уравнения n-го порядка. Фундаментальная система решений. Структура общего решения. Определитель Вронского. Система линейных уравнений.
- •I.3. Первая краевая задача для лоу 2-го порядка. Функция Грина.
- •I.4. Устойчивость по Ляпунову. Теорема Ляпунова об устойчивости по первому приближению.
- •II.1. Гильберта разрешимости 1 краевой задачи для обыкновенного дифференциального уравнения 2-го порядка.
- •II.2. Теорема о структуре общего решения лин-го ду n-го порядка.
- •II.3.Теорема Пикара и Пеано.
- •I.1. Производная, дифференцируемость и дифференциал. Правила дифференцирования.
- •I.2. Неопределённый интеграл. Основные методы интегрирования.
- •I.3. Числовой ряд. Сходимость.
- •I.4. Криволинейный интеграл. Формула Грина.
- •I.5. Формулы и ряд Тейлора.
- •I.6. Примеры разложения функции в ряд Тейлора.
- •I.7. Интеграл Римана и его свойства.
- •I.8. Тригонометрический ряд. Ряд Фурье.
- •I.9. Двойной интеграл. Вычисление интеграла.
- •I.10. Функциональный ряд. Точечная и равномерная сходимости.
- •II.1. Непрерывные функции. Свойства функций непрерывных на компакте.
- •II.2. Локальный экстремум функций одной переменной. Необходимые условия. Достаточные условия.
- •II.3. Интеграл Римана. Формула Ньютона-Лейбница.
- •II.4. Дифференцируемость функции нескольких переменных. Необходимые условия. Достаточные условия.
- •II.5. Формула Тейлора. Ряд Тейлора. Необходимые и достаточные условия представления функции рядом Тейлора.
- •I.1. План злп. Опорный план.
- •I.2. Канонический вид злп.
- •I.3. Двойственная злп.
- •I.4. Методы возможных направлений.
- •II.1. Теоремы двойственности в линейном программировании.
- •II.2. Теорема об оптимальности в симплекс-методе.
- •I.1. Переменные, массивы и указатели базовых и производных типов, инициализация, допустимые операции над ними.
- •I.2. Циклы, вложенные циклы, операторы циклов, подготовка и изменение переменных в циклах.
- •I.3. Функции, их определение, формальные параметры, прототипы. Методы передачи информации в функцию и из функции. Проектирование и составление программ модульной структуры.
- •I.4. Классы, секции доступа. Данные-члены, функции-члены, дружественные функции.
- •I.5. Объекты, их массивы, указатели на них.
- •I.6. Конструкторы и деструкторы.
- •I.7. Полиморфизм в программировании. Перегрузка функций, знаков операций. Действия над объектами.
- •II.1. Методика проектирования и составления программ модульной структуры.
- •II.2. Выражения, операции над величинами базовых типов.
- •II.3. Методика программирования простых и вложенных типов.
- •Численные методы
- •I.1. Задача теории интерполирования функции. Система функций Чебышева.
- •I.2. Интерполяционные квадратурные формулы Ньютона-Котеса.
- •I.3. Методы итераций для нелинейного ур-ия (хорд и Ньютона).
- •I.4. Методы итераций для систем лин. Ур-ий. Условия сходимости.
- •I.5. Задача Коши для оду. Методы Рунге-Кутта (принцип построения, пример).
- •II.1. Интерполяционный многочлен Лагранжа. Геометр-ий смысл.
- •II.2. Вывод простой и обобщённой формулы трапеции. Погрешность формулы.
- •II.3. Метод хорд для решения нелинейных уравнений. Условие применимости метода, сходимость.
- •II.4. Метод касательных для решения нелинейных уравнений, условие применимости метода.
- •II.5. Метод итераций для решения систем линейных алгебраических уравнений. Сходимость метода.
- •II.6. Одношаговые методы решения задач Коши. Метод Эйлера.
- •II.7. Одношаговые методы решения задачи Коши. Формулы Рунге-Кутта.
II.5. Эйлеровы графы. Критерий эйлеровости графов.

Цикл, содержащий все рёбра графа, наз-ся эйлеровым циклом, а граф, содержащий эйлеровый цикл – эйлеровым графом.
Критерий эйлеровости графов.
Граф G является эйлеровым графом , когда он связан и степени его вершин чётные.
Необходимость: Если граф G содержит эйлеровый цикл, то 2 его вершины лежат на этом цикле, т.е. граф – связный и степени его вершин чётные.
Докво.
При обходе цикла в k
вершину “входили” по одному ребру и
“выходили” по другому 1,2 или k
раз. Значит, степень
вершины чётная. Пусть а1
– некоторая вершина графа, аi
– смежная ей вершина, которой инцидентно
хотя бы одно ребро (аi,аj)
отличное от (а1,аi).
Вершине аj
найдётся хотя бы одно инцидентное ребро
![]() Построим
из этих рёбер цепь, отличая рёбра и не
повторяя их. Т.к. граф G
– конечный, эта цепь должна закончиться
в некоторой вершине а2.
Число рёбер, инцидентных вершине а2,
тоже чётно по условию теоремы, т.е. мы
построили цикл Z1,
причём, если в графе G
остались неотмеченные рёбра, то среди
них найдётся хотя бы одно инцидентное
какоё-нибудь вершине на Z1
(т.к. G
– связный). Пусть эта вершина b1.
Построим
из этих рёбер цепь, отличая рёбра и не
повторяя их. Т.к. граф G
– конечный, эта цепь должна закончиться
в некоторой вершине а2.
Число рёбер, инцидентных вершине а2,
тоже чётно по условию теоремы, т.е. мы
построили цикл Z1,
причём, если в графе G
остались неотмеченные рёбра, то среди
них найдётся хотя бы одно инцидентное
какоё-нибудь вершине на Z1
(т.к. G
– связный). Пусть эта вершина b1.
Достаточность: Пусть G – связный граф и степень его вершины чётная, то построим эйлеровый цикл на этом графе.
Докво. Начиная из вершины b1, как и на 1ом шаге, строим цикл Z2 из рёбер не вошедших в Z1. Из циклов Z1 и Z2 можно построить один новый цикл, проходящий из а1 в b1 по части Z1, затем по всему циклу Z2, а потом на оставшейся части Z1. Т.к. граф G конечен, то, совершив конечное число таких шагов, построим эйлеров цикл.
П.6. Теорема о полноте системы булевых функций.
Пусть
даны две системы булевых функций
![]() и система F
полна, если при этом каждую функцию этой
системы можно выразить через функции
системы G,
то система G
тоже является полной.
и система F
полна, если при этом каждую функцию этой
системы можно выразить через функции
системы G,
то система G
тоже является полной.
Докво.
т.к.
F
полная система, то произвольную булеву
функцию h(x)
можно выразить через функции системы
F
в виде формулы
![]() ;
по условию
;
по условию
![]() после подстановки получаем:
после подстановки получаем:
![]() ,
т.е. произвольную Булеву функцию h(x)
можно выразить через функции системы
G,
значит G-полная
(через неё что угодно можно выразить).
Данная теорема позволяет расширить
список примеров полных систем: 1)
,
т.е. произвольную Булеву функцию h(x)
можно выразить через функции системы
G,
значит G-полная
(через неё что угодно можно выразить).
Данная теорема позволяет расширить
список примеров полных систем: 1)
![]() ,
2)
,
2)
![]()
![]() ,
,
3)
![]() ,
4)
,
4)
![]()
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
I.1. Постановка задачи Коши для оду n-го порядка. Достаточные условия разрешимости
Среди
всех решений уравнения![]() найти такое, которое удовлетворяет
условию Коши:
найти такое, которое удовлетворяет
условию Коши:
![]() ,
т.е
,
т.е
![]() где
где
![]() -
заданные
действительные числа.
-
заданные
действительные числа.
Достаточное условие разрешимости(условие выполнение Липшица по у):
Если
в области
![]() выпуклый
по у
выпуклый
по у
![]() ограниченная
ограниченная
![]() (область
(область
![]() называется
выпуклой по у, если она содержит целиком
отрезок прямой соединяющий точки
называется
выпуклой по у, если она содержит целиком
отрезок прямой соединяющий точки
![]() принадлежащие этому множеству)
принадлежащие этому множеству)
I.2. Линейные уравнения n-го порядка. Фундаментальная система решений. Структура общего решения. Определитель Вронского. Система линейных уравнений.
Линейным
дифференциальным уравнением n-го
порядка
наз-ся уравнение:![]() где
a1(t),…an(t),
g(t)
определены на некотором отрезке [a,b].
где
a1(t),…an(t),
g(t)
определены на некотором отрезке [a,b].
Линейное
диф-ое ур-ие (1) порядка n
сводится к линейной
системе
первого
порядка из n
дифференциальных ур-ий:
![]() где
где

Система из n решений уравнения (2), линейно независимых на отрезке [a,b], наз-ся фундаментальной системой.
Структура
общего решения ЛОС:![]()
ЛНС:![]() Ci=const,{yi(x)}
– ФСР ЛОС.
Ci=const,{yi(x)}
– ФСР ЛОС.
Определителем
Вронского
системы решений y1(t),…,yn(t)
уравнения
![]() называется
определитель:
называется
определитель: