3. Зсув (зріз). Напруження та деформації. Розрахунки на міцність

На деформацію зсуву (зрізу) працює більшість з’єднань, навантажених поперечними силами: різьбові, шпонкові, заклепкові, зварні та інші.

Зсувом називається такий вид деформації, при якому в поперечних перерізах тіла діє тільки внутрішня поперечна сила і пов’язані з нею дотичні напруження τ.

Д

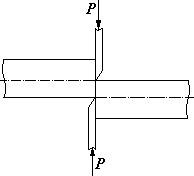
Рис.1.6. Деформація зсуву.

Схема дії сил зрізу

еформація зсуву (рис.1.6) полягає в перекошуванні прямих кутів прямокутника, що знаходиться між лініями дії двох дуже близько розташованих поперечних сил, напрямлених назустріч одна одній. При деформації зсуву має місце тільки зміна форми тіла.

У поперечних перерізах виникають дотичні напруження, які в усіх точках перерізу однакові й визначаються за формулою:

,

де P – поперечна сила в перерізі; А – площа поперечного перерізу бруса.

Абсолютна деформація ΔS – це зміщення площини поперечного перерізу відносно його початкового положення (рис.1.7).

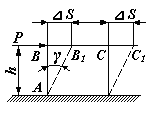
Рис.1.7. Абсолютна S і відносна  деформації при зсуві

Кут 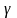, на який змінюється початковий прямий кут, називається кутом зсуву або відносним зсувом. З трикутника ВАВ₁, враховуючи малість кута , можна вважати, що

,

де 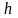– висота поперечного перерізу.

Залежність між параметрами деформації зсуву і напруженнями, які їх спричиняють, виражається законом Гука:

,

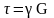де τ – дотичні напруження, які виникають у поперечних перерізах; γ – відносний зсув; 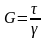є величина стала для окремо взятого матеріалу і називається модулем пружності другого роду.

Підставляючи замість , а замість 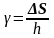у формулу закону Гука, отримаємо закон Гука для абсолютного зсуву:

.

Умову міцності для деформації зсуву (зрізу) в загальному вигляді записують:

,

де τ_max – максимальні напруження, які виникають у поперечних перерізах; i – кількість площин зрізу; n – кількість елементів, які одночасно працюють на деформацію зрізу; [τ] – допустимі напруження.

За допомогою умови міцності при проектувальному розрахунку визначають площу поперечного перерізу, задаючись кількістю одночасно працюючих елементів, або навпаки.

4. Кручення. Напруження та деформації. Розрахунки на міцність і жорсткість

На деформацію кручення працюють багато елементів машин і механізмів: вали, рами автомобілів, фрези, свердла, окремі частини станин металорізальних верстатів.

Основні залежності при крученні круглих брусів. Деформацію кручення викликає тільки один силовий фактор, який виникає в поперечному перерізі бруса – крутний момент М_кр.. Величина крутного моменту в довільному перерізі бруса дорівнює алгебраїчній сумі крутних моментів, прикладених по один бік перерізу. Крутний момент, що діє за ходом годинникової стрілки (якщо дивитись з лівого торця бруса), записують зі знаком „+”, проти – зі знаком „–”.

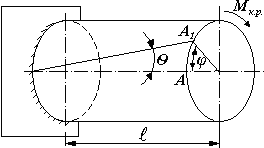
Рис.1.8. Деформації при крученні

При деформації кручення відбувається взаємний поворот торцевих перерізів на кут, який називається абсолютним кутом закручення φ (рис.1.8). Абсолютний кут закручення визначається за формулою:

φ= ,

де l – довжина ділянки; G – модуль пружності II роду; І_р – полярний момент інерції площі поперечного перерізу відносно полюса.

Для круглого суцільного перерізу:

.

Для кільцевого перерізу:

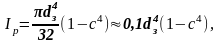
де , d_з i d_вн – відповідно зовнішній і внутрішній діаметри кільця.

Деформацію кручення можна визначити також відносним кутом закручення θ. Для ділянки зі сталим крутним моментом і жорсткістю:

θ .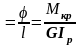

Умови жорсткості:

.

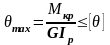У поперечних розрізах при крученні бруса круглого поперечного перерізу виникають тільки дотичні напруження. Величина дотичного напруження прямо пропорційна відстані ρ від центра ваги перерізу (рис.1.9) і обчислюється за формулою:

,

де W_p= – полярний момент опору площі поперечного перерізу відносно полюса. Для суцільного перерізу:

.

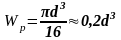Умова міцності:

,

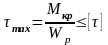де [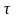 ] – допустиме дотичне напруження при крученні:

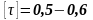[ _p],

де [ _p] – допустиме напруження на розтяг.

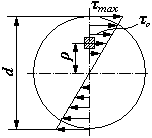
Рис.1.9. Епюра дотичних напружень у круглому поперечному перерізі вала.

При розрахунку валів на деформацію кручення з умови міцності визначають діаметр d вала:

,

а потім перевіряють його на жорсткість:

.
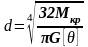