1.Понятие функции. Способы задания функций

2.Классификации функций.

3.Область определения функции. Четность и периодичность функций.

4.Обратные функции. Понятия сложной функции, явной и неявной функций.

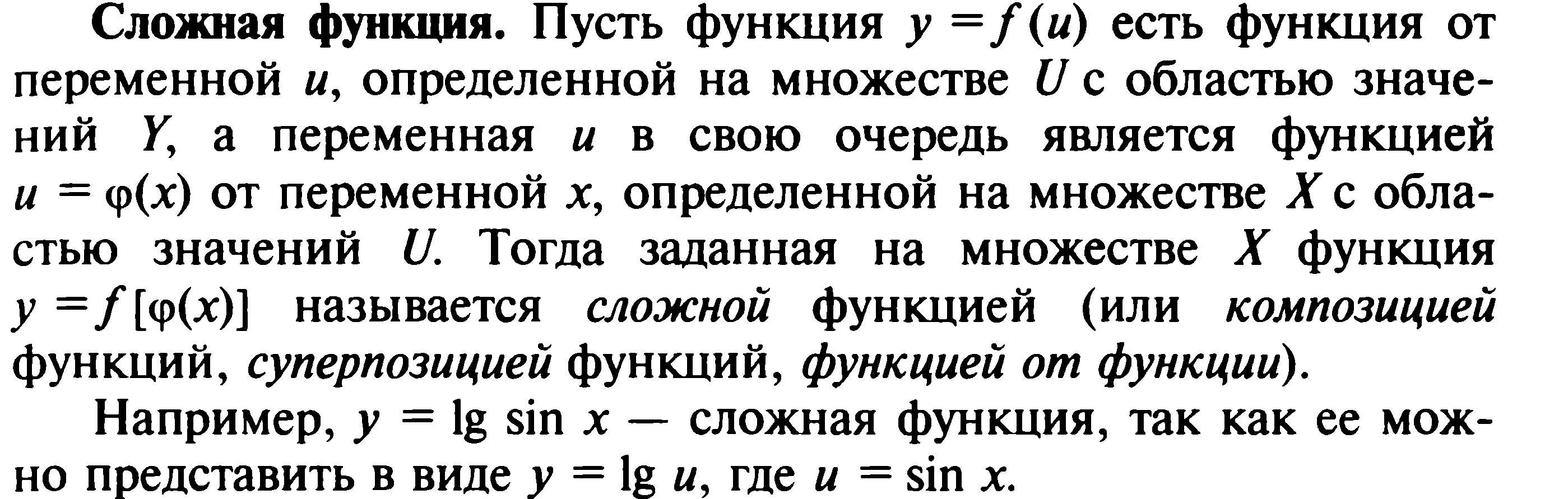
5.Преобразование графиков функций.

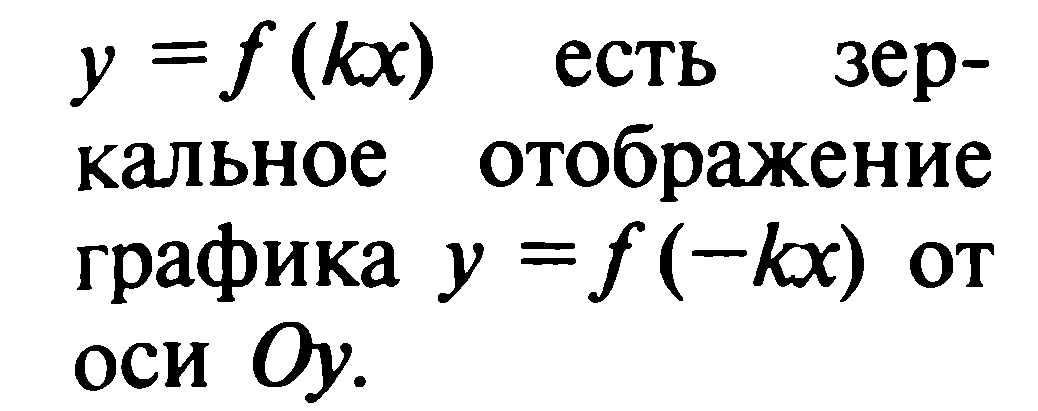
6.Применение функций в экономике.

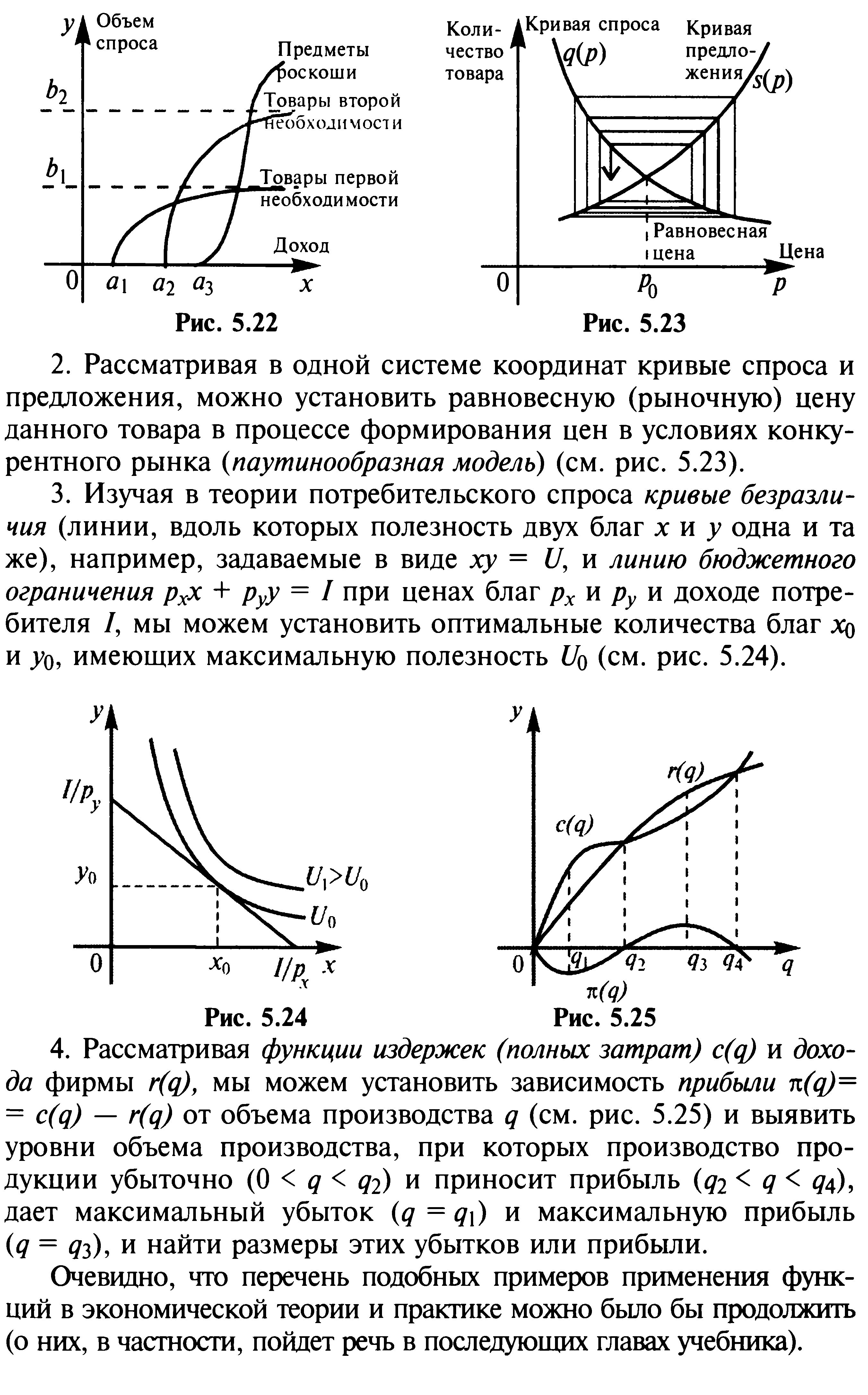
7.Предел числовой последовательности.

8.Предел функции в точке. Предел функции на бесконечности.

9.Основные теоремы о пределах.

10.Бесконечно малые функции и их основные свойства.

11.Бесконечно большие функции и их основные свойства.

12.Связь между бесконечно малыми и бесконечно большими функциями.

13.Раскрытие некоторых типов неопределенностей.

Раскрывать неопределенности позволяет:

упрощение вида функции (преобразование выражения с использованием формул сокращенного умножения, тригонометрических формул, домножением на сопряженные выражения с последующим сокращением и т.п.);

использование замечательных пределов;

применение правила Лопиталя;

использование замены бесконечно малого выражения ему эквивалентным (использование таблицы эквивалентных бесконечно малых).

Теорема Лопита́ля— метод нахождения пределов функций, раскрывающий неопределённости вида 0/0 и беск/беск. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.

Пусть функции y=f(x) и y=g(x) удовл следующим условиям:

1) эти функции дифференцируемы в окрестности точки a,кроме,может быть, самой точки a;

2) и в этой окрестности;

3) ;

4) существует конечный или бесконечный.

Тогда существует и , причем формула

Таким образом, вычисление предела отношения двух функций может быть заменено при выполнении условий теоремы вычислением предела отношения производных этих функций

Пример:

14.1-й 2-й замечательные пределы.

1.

график функции выглядит так

2!

15.Односторонние пределы функции.

Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами.

1)Предел слева

Число A называется пределом функции y=f(x) слева в точке х₀, если для любого положительного числа существует такое число , что при , выполняется неравенство

Записывается так:

2)Предел справа

Число A называется пределом функции y=f(x)слева в точке х₀, если для любого положительного числа существует такое число , что при , выполняется неравенство

Записывается так:

16.Непрерывность функции (два определения).Примеры.

17. Виды разрывов функции.

18.Сравнение порядков бесконечно малых функций.

Пусть а=а(х) и в=в(х)-бесконечно малые при х стрем к х₀, т.е и тогда:

-А и В-б м одного порядка

-А б м более высокого порядка, чем В

-А б м более низкого порядка, чем В

=не существует-А и В несравнимые бесконечно малые.

Пример: сравнить порядок функций и В=14х² при

следовательно эти бесконечно малые функции одного порядка.

19.Эквивалентные бесконечно малые функции.

Если то α и ß называются эквивалентными бесконечно малыми (при х→x₀); это обозначается:α~ß. Например, sinx~х при х→0 т.к при x→0, т. к

sinx~х при х→0;

tgx~х (х→0);

arcsinх ~ х (х→0);

arctgx~х (х→0);

1-cosx~x2/2 (х→0);

ех-1~х (х→0);

αх-1~х*ln(a) (х→0);

ln(1+х)~х (х→0);

loga(l+х)~х•logaе (х→0);

(1+х)k-1~k*х, k>0 ⁽Для раскрытия неопределённостей вида 0/0 часто бывают полезным применять принцип замены бесконечно малых эквивалентными х→0);

Производная функции в точке, ее геометрический смысл.

Определение. Производной функции у = f{x) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю {если этот предел существует):

Н𝜟хождение производной функции называется дифференцированием этой функции.

Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке. геометрический смысл производной: производная есть угловой коэффициент {тангенс угла наклона) касательной, проведенной к кривой y=f{x) в точке

Тогда уравнение касательной к кривой примет вид

Производная алгебраической суммы функций, произведения и частного.

Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих

функций, т.е.

Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т.е.

Производная частного двух дифференцируемых функций может быть найдена по формуле

Общая схема н𝜟хождения производных функций.

Производная функции у =f(x) может быть найдена по следующей схеме:

1. Дадим аргументу х приращение и найдем наращен-

ное значение функции

2. Н𝜟ходим приращение функции

3. Составляем отношение

4. Н𝜟ходим предел этого отношения при , т.е.

(это не к вопросу, но знать нужно)

Правило дифференцирования сложной функции.

Пусть переменная у есть функция от переменной а переменная u в свою очередь есть функция от независимой переменной х:, т.е. задана сложная функция

Теорема. Если — дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и, умноженной на производную самого промежуточного

аргумента по независимой переменной х, т.е.

Правило дифференцирования сложной функции может

быть записано и в других форм𝜟х:

Логарифмическое дифференцирование.

Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала н𝜟ходится логарифм функции, а затем вычисляется производная от него. Такой прием можно использовать для н𝜟хождения производных степенных, рациональных и некоторых иррациональных функций.

Рассмотрим этот подход более детально. Пусть дана функция y = f(x). Возьмем натуральные логарифмы от обеих частей:

Теперь продифференцируем это выражение как сложную функцию, имея ввиду, что y - это функция от x.

Отсюда видно, что искомая производная равна

Такая производная от логарифма функции называется логарифмической производной.

Данный метод позволяет также эффективно вычислять производные показательно-степенных функций, то есть функций вида

где u(x) и v(x) − дифференцируемые функции от x.

Дифференцирование неявных функций.

Рассмотрим дифференцирование неявной функции, заданной урав-

нением F{x, у) = 0

Для н𝜟хождения производной функции у, заданной неявно, нужно продифференцировать обе части уравнения, рассматривая у как функцию от х, а затем из полученного уравнения найти производную у'.

Найти производную функции у, заданной уравнением , и вычислить ее значение в точке (2; 1).

Решение. Дифференцируя обе части равенства и учитывая,

что у есть функция от х, получим , откуда