Контрольні питання

1. Що називається інтерференцією світла?

2. Які хвилі називаються когерентними?

3. Умова підсилення і послаблення світла в інтерференції.

4. Роль біпризми в цій роботі.

5. Вивести робочу формулу.

Лабораторна робота № 106

Визначення сталої дифракційної гратки та довжини світлової хвилі

Прилади і матеріали: освітлювач, світлофільтри, пластинка з отворами, дифракційна гратка, рамка.

Мета роботи: оволодіти методикою визначення довжини хвилі світла за допомогою дифракційної гратки.

І. Теоретичні відомості

Явище відхилення світла від прямолінійного поширення при огинанні перешкоди називається дифракцією світла. Дифракційну картину можна отримати за допомогою дифракційної гратки, яка являє собою сукупність великого числа паралельних рівновіддалених одна від одної щілин. У найпростішому варіанті такою граткою є скляна пластина, на якій за допомогою ділильного пристрою через рівні проміжки нанесено паралельні лінії – подряпини. На довжині в один міліметр їх можна нанести понад 1000. Ці подряпини розсіюють світло, не пропускаючи його, а проміжки між ними є щілинами, що пропускають світло.

На рис. 1 схематично зображено дифракційну гратку г: а – ши­рина щілини; b – ширина непрозорої частини між щілинами; d = a + b –

п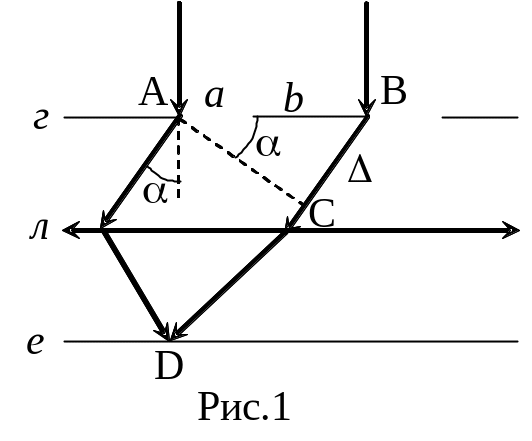 еріод (стала) дифракційної гратки. Нехай на дифракційну гратку з двома щілинами падає монохроматичний пучок паралель­них світлових променів. Ці щілини є когерентними джерелами світла. Якщо за дифракційною граткою г розташувати збір­ну лінзу л, то на екрані е, що міститься у фокальній площині лінзи, одержимо диф­ракційну картину. Дифракційна картина є результатом двох процесів: 1) дифракції світла від кожної щілини зокрема; 2) інтерференції від обох щілин.

Розглянемо інтерференцію від обох щілин, взявши для простоти два промені, що падають на ліві краї щілини і дифрагують під кутом . З рис. 2 бачимо, що різниця ходу  = ВС = АВsin, тобто

 = d sin . (1)

Якщо  дорівнює непарному числу півхвиль (2k + 1)/2, то в розглядуваній точці D екрана отримаємо мінімум:

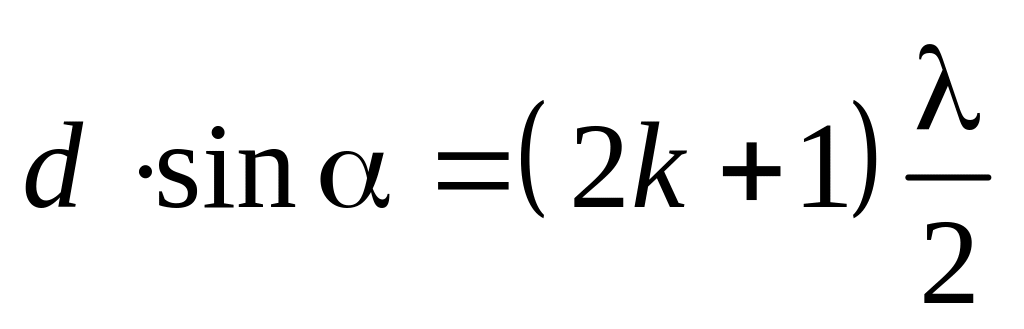, k = 0, 1, 2, 3,… (2)

Якщо різниця ходу  дорівнює парному числу півхвиль 2k , то в розглядуваній точці D екрана отримаємо максимум:

, k = 0, 1, 2, 3,… (3)

Рівняння (3) залишається справедливим у випадку багатьох щілин і називається формулою дифракційної гратки.

Якщо освітити щілину білим світлом, то для кожної з його складових (монохроматичних хвиль) при даному k одержимо свій максимум. Для максимуму нульового порядку (k = 0) різниця ходу  для хвиль будь-якої довжини дорівнює нулю. Тому на екрані навпроти середини дифракційної гратки буде спостерігатися смуга білого кольору (центральний максимум). По обидва боки від центрального максимуму, чергуючись із темними смугами (мінімумами), симетрично розташуються спектрально забарвлені смуги (максимуми) 1-го, 2-го, 3-го та інших порядків. Ближче до нульового максимуму будуть знаходитися зони фіолетового кольору (з найменшою ), з протилежного боку – зони червоного кольору (з найбільшою ). Між фіолетовим та червоним краями кожного максимуму розмістяться всі інші спектральні кольори. У зв’язку з цим дифракційні максимуми називаються дифракційними спектрами.

Якщо пучок паралельних монохроматичних променів падає перпендикулярно екрану В з двома паралельними щілинами, що знаходяться на відстані d одна від одної, то ці щілини стають когерентними джерелами світла.

Якщо за екраном В (рис.2б) помістити збірну лінзу С, то на екрані А, розташованому у фокальній площині лінзи, виникне дифракційна картина, що є результатом двох процесів: дифракції світла від кожної окремої щілини і інтерференції світла від обох щілин. Головні риси цієї картини визначаються іншим процесом.

Розглянемо промені, що падають, наприклад, на ліві краї обох щілин. Внаслідок дифракції світло від щілин буде розповсюджуватися в усіх можливих напрямках (рис.1б,а). З рис.1б видно, що різниця ходу паралельних променів, що дифрагують від щілин під кутом , дорівнює:

l = d sin . (4)

Зібрані лінзою С в одну точку D екрану A, ці хвилі проінтерферують; результат інтерференції буде залежати від різниці ходу . При різниці ходу, рівній цілому числу хвиль, згідно з формулою (3), промені утворять на екрані А інтерференційний максимум. При різниці ходу, рівній непарному числу півхвиль, тобто за умови d sin =( 2n+1) /2, промені дадуть на екрані інтерференційний мінімум.

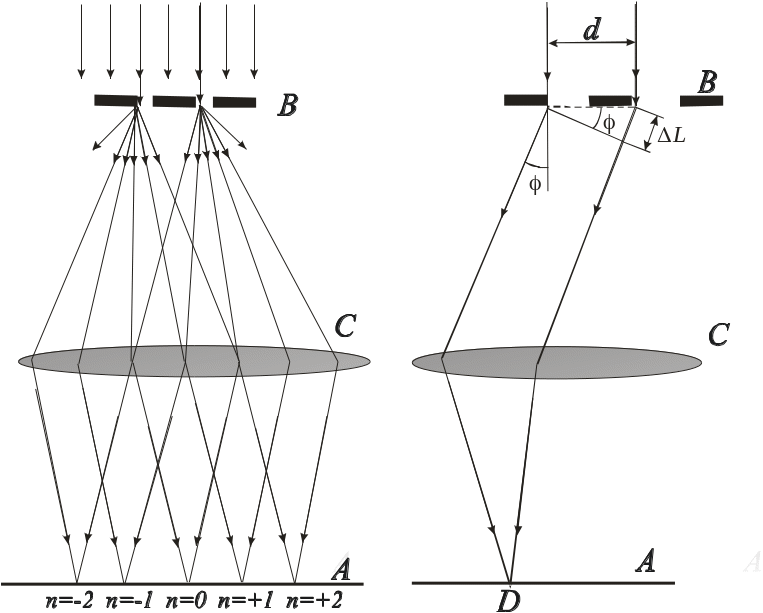
а) б)

Рис.2.

Кути дифракції, що відповідають максимумам освітленості екрана визначаються зі співвідношення

sin = n / d, (5)

а мінімумам освітленості – зі співвідношення

sin = ( 2n+1) /2a, (6)

де n – цілі (додатні і від‘ємні) числа (n= 0,1,2,3). Згідно з формулою (3) по обидва боки від центрального максимуму, якому відповідає значення n=0, знаходяться перші побічні максимуми – правий (n=+1) і лівий (n=-1), далі знаходяться другі максимуми (n=+2; n=-2) і т.д. Кількість цих побічних максимумів є обмежена і не більша ніж d/ . Освітленість E різних максимумів неоднакова і зменшується при збільшенні кута дифракції (мал.3).

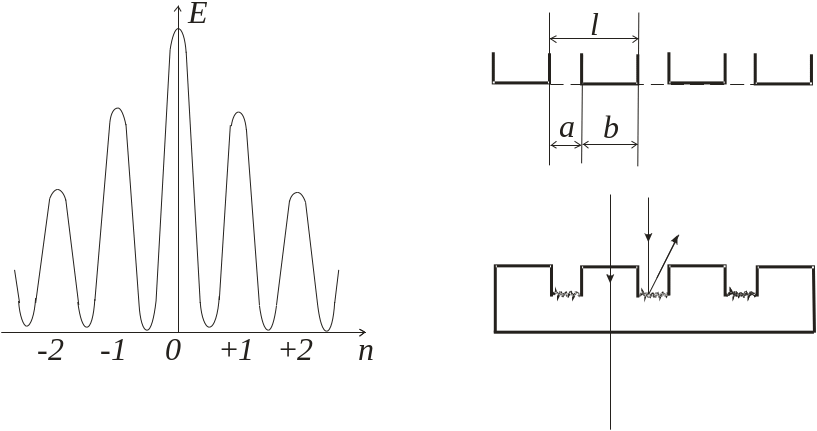
Рис.3. Рис.4.

При дифракції світла від сукупності багатьох паралельних щілин, розташованих близько одна від одної, створюється така ж дифракційна картина, як і у випадку двох щілин. Лише максимуми одержуються більш яскравими і вузькими, а мінімуми, що їх розділяють - широкими і практично зовсім темними.

Формула (3), що визначає місцезнаходження максимумів при дифракції від двох щілин, залишається справедливою і у випадку багатьох щілин.

Дифракційна гратка – це сукупність великої кількості вузьких паралельних щілин, розташованих близько одна від одної (рис.4). Згідно з рис.4 формула (3) запишеться у вигляді:

(a+b) sin = n , (7)

де n =1,2,3…порядок спектра, а – ширина щілини, b – ширина непрозорого проміжку, (a+b) – стала гратки, або період гратки.

З формули (7) отримаємо:

= (a+b) sin /n, (8)

тобто короткі хвилі відхиляються дифракційною граткою менше, ніж довгі хвилі. Тому при проходженні через дифракційну гратку білого світла одержується дифракційний спектр, в якому фіолетова частина відхилена менше, ніж червона в протилежність до спектра, одержаного за допомогою призми.