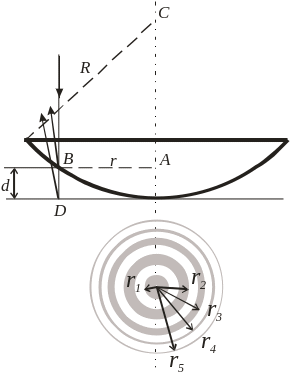Іі. Завдання

1. Визначити числову апертуру та роздільну здатність мікроскопа.

III. Хід роботи

1. Увімкнути освітлювач в електромережу і відрегулювати освітлення.

2. Закріпити металеву пластинку з отвором на предметному столику так, щоб центр отвору приблизно співпадав з оптичною віссю мікроскопа.

3. Навести мікроскоп так, щоб чітко було видно отвір.

4. Відвести вбік освітлюване дзеркало і встановити лінійку АВ з ковзними покажчиками під столиком мікроскопа .

Вийняти окуляр і виміряти діаметр отвору за допомогою лінійки з ковзними покажчиками. З рис.2 видно, що

sin u/2=AD/AO. (9)

АD вимірюємо лінійкою з ковзними покажчиками.

Щоб визначити АО, потрібно масштабною лінійкою виміряти ОD (тобто висоту пластинки над лінійкою з ковзними покажчиками) і за теоремою Піфагора обчислити АО. Досліди проробити не менше 5 разів.

5. За формулами (8,9) обчислити числову апертуру і роздільну здатність.

6. Дані занести в табл. 1.

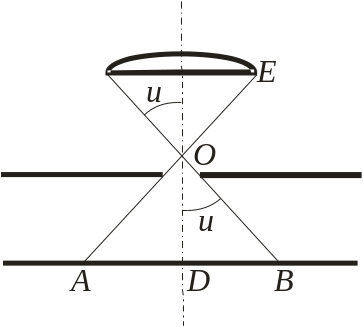
Рис.2.

Таблиця 1

Результати вимірювань та обчислень

№	АВ, мм	АD, мм	ОD, мм	АО, мм	sin u/2	Δу	Δ(∆y)

Контрольні питання

1. Яка будова мікроскопа?

2. Зобразити хід променів у мікроскопі.

3. Що таке роздільна здатність мікроскопа?

4. Як підвищити роздільну здатність мікроскопа?

5. Що таке апертурний кут?

6. За якою формулою обчислюється числова апертура?

7. Обчисліть межу роздільної здатності мікроскопа імерсійної системи при прямому освітленні, якщо між покривним склом і об’єктивом поміщена крапля кедрової олії, для якої n=1,5.

8. Як змінюється довжина світлової хвилі при переході з одного середовища в інше?

Лабораторна робота № 104

Визначення радіуса кривизни лінзи за допомогою кілець ньютона

Прилади і матеріали: установка для одержання та дослідження кілець Ньютона.

Мета роботи: оволодіти методикою визначення радіуса кривизни лінзи за допомогою дослідження кілець Ньютона.

І. Теоретичні відомості

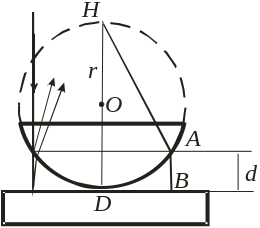
Інтерференційні кільця Ньютона виникають при освітленні плоско-опуклої лінзи досить великого радіуса кривизни, що лежить випуклою поверхнею на плоско-паралельній скляній пластинці (рис.1). Причина утворення кілець Ньютона полягає в тому, що між плоскою поверхнею скла і опуклою поверхнею лінзи знаходиться повітря, і цей повітряний шар є тонкою пластинкою, товщина якої збільшується від центра до країв. Інтерференцією світлових хвиль, що сходяться в деякій точці простору, спостерігають, якщо ці хвилі є когерентними (при однаковій частоті мають сталу різницю фаз).

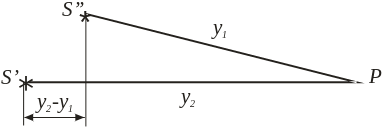
Розглянемо інтерференцію двох хвиль однакової амплітуди, що виходять з когерентних джерел S^/ і S^// і зустрічаються в точці Р (рис.2).

Рис.1.	Рис.2.

Зміщення, що виникають в точці Р від першої і другої хвилі, відповідно дорівнюють

X₁ = A sin( t + 2πy₁/ ), ( t + 2πy₁/ ) = ₁

X₂= A sin( t + 2πy₂/ ), ( t + 2πy₂/ ) = _2. (1)

Тоді результат додавання визначиться різницею фаз = ₁ - ₂ =2π(y₁-y₂)/ . Якщо

2π (y₁-y₂)/ =2πn, (2)

то в точці Р спостерігається максимум, коливання максимально підсилять одне одного і результуюча амплітуда буде 2А. Якщо ж

2π (y₁-y₂)/ =(2n+1) π, (3)

де n = 0,1,2,3…, то в точці Р буде мінімум, коливання взаємно погасяться і результуюча амплітуда в цьому випадку рівна нулю.

Умови максимуму (2) і мінімуму (3) можна ще записати у вигляді:

mах: =y₁-y₂=nπ=2n /2, (4)

mіn: =y₁-y₂=(2n+1) /2, (5)

де =y₁-y₂ – різниця ходу хвиль, або різниця ходу променів.

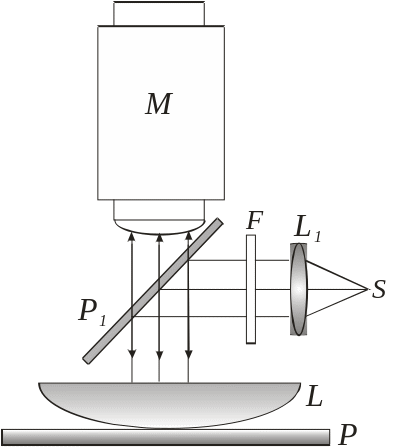
Отже, в точці Р буде mах, якщо різниця ходу хвиль складає парне число півхвиль (ціле число хвиль), а mіn – коли різниця ходу складає непарне число півхвиль. Інтерференційну картину від клина змінної товщини вперше вивчав Ньютон. Схема спостереження кілець Ньютона зображена на рис.3.

Рис.3.	Рис.4.

Пучок паралельних променів падає зверху на лінзу великого радіуса кривизни. Світлова хвиля, що доходить до точки В, частково відбивається, а частково проходить у повітряний клин (практично вертикально, через малу кривизну лінзи). Відбиваючись в точці D від пластинки, вона повертається назад і інтерферує з хвилею, відбитою в точці В. Змінна ширина повітряного клина d залежить від розташування точки В, що характеризується радіусом r. З прямокутного АВС маємо:

r²=R²-(R-d)²=(2R-d) (при умові d<R).

Отже, d=r²/2R. (6)

Оскільки в точці D є відбивання від оптично більш густого середовища і втрачається півхвилі, то оптична різниця ходу обох інтерферуючих відбитих хвиль буде:

=2d + /2 = r²/R + ₀/2. (7)

При освітленні системи монохроматичними променями у відбитому світлі будуть спостерігатися світлі і темні кільця сталих радіусів r=const. Радіуси темних кілець визначаються з умови міn.

=(2k +1) /2, тобто r²/R + /2= k + /2, (8)

звідки r_Т= .

Радіуси світлих кілець знаходять з умови максимумів:

=2k /2; r_cb= (9)

Вимірюючи радіуси кілець r і знаючи довжину хвилі , можна визначити радіус кривизни лінзи R.

Розглянемо світлі кільця, номери яких , відраховуючи від центра, позначимо “n” і “m” , для яких різниця ходу дорівнює

=2d_m + /2 =m , (10)

звідки товщина повітряного шару

d_m =m /2 - /4. (11)

=2d_n + /2 =n , (12)

звідки товщина повітряного шару

d_n=n /2 - /4. (13)

Різниця в товщині повітряного шару для тих місць, де ці кільця спостерігаються, буде:

d_m – d_n = = (14)

З другого боку, товщина повітряного шару для цих кілець може бути визначена через радіус кілець формулами:

d_m= ; d_n= , (15)

а різниця в товщині повітряного шару кілець цих радіусів дорівнює:

(16)

Порівнюючи рівняння (14) і (15), одержимо:

, (17)

Це й буде робочою формулою, яка є дійсною як у випадку світлих, так і темних кілець Ньютона.

Різницю між кільцями необхідно вибирати якнайбільшою, наприклад, перше з сьомим, друге з восьмим і т.д.